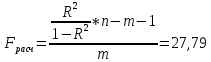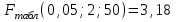Множественная регрессия
1. Составить корреляционную матрицу, провести ее анализ. Исследовать интеркорреляцию переменных.
Элементами данной матрицы являются коэффициенты парной корреляции. Элементы, стоящие на главной диагонали, равны 1. Следовательно:
  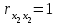 
Элементы, стоящие симметрично относительно главной диагонали, равны.
Расчеты проводились с помощью ППП «Анализ данных» MS Excel. Корреляционная матрица имеет вид:
|
Y
|
X1
|
X2
|
X3
|
X4
|
X5
|
Y
|
1
|
|
|
|
|
|
X1
|
0,71950
|
1
|
|
|
|
|
X2
|
-0,01862
|
0,10395
|
1
|
|
|
|
X3
|
0,36528
|
-0,11145
|
-0,28159
|
1
|
|
|
X4
|
0,03103
|
0,31555
|
-0,02275
|
-0,10268
|
1
|
|
X5
|
-0,32970
|
-0,28930
|
-0,37752
|
0,03736
|
0,00112
|
1
|
Анализ корреляционной матрицы показывает, что независимые переменные в основном слабо связаны между собой (коэффициенты межфакторной корреляции по абсолютному значению меньше 0,7), сильная связь наблюдается только между факторами х1 и Y. С результативным показателем y них связь тоже слабая.
2. Найти коэффициенты множественной детерминации и корреляции, сделать вывод.
Коэффициент множественной детерминации найдем по формуле
 0,263 0,263
Коэффициент множественной детерминации показывает, что изменение значений y на 26% объясняется признаками x1, x2, x3, x4, x5.
Коэффициент множественной корреляции равен:
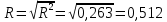
Коэффициент множественной корреляции, равный 0,512, свидетельствует о том, что между y и факторами x1, x2, x3, x4, x5 существует слабая регрессионная связь.
3. Оставить в модели множественной регрессии две независимые переменные.
Как показывает анализ корреляционной матрицы, факторы оказывают слабое влияние на результирующий фактор Y, наибольшее влияние на Y оказывает фактор X1 (коэффициент корреляции 0,719).
4. Построить уравнение множественной регрессии по двум независимым переменным. Оценить точность модели. Проверить статистическую значимость уравнения множественной регрессии в целом. Найти коэффициенты множественной детерминации и корреляции.
Уравнение множественной линейной регрессии по двум объясняющим переменным имеет вид (см. приложение 3)
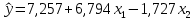
Средняя относительная ошибка аппроксимации равна
 =28,35 =28,35
расчёты приведены в таблице (см. приложение 4).
Т.к. значения средней относительной ошибки аппроксимации для уравнения > 12%, уравнениe не даёт хорошую точность.
Коэффициент множественной детерминации равен
R2=0,526
Коэффициент множественной детерминации показывает, что изменение значений Y на 52% объясняется признаками х1 и х2.
Коэффициент множественной корреляции будет равен:

Коэффициент множественной корреляции, равный 0,725, показывает, что связь между показателями слабая.
Исследуем статистическую значимость уравнения множественной регрессии в целом, используя F-критерий Фишера.
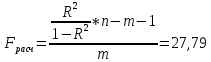
α=0,05
k1=m=2
k2=n-m-1=50
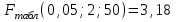
Поскольку Fрасч>Fтабл, уравнение множественной регрессии в целом является статистически значимым.
Приложение 1.
ВЫВОД ИТОГОВ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная статистика
|
|
|
|
|
|
|
Множественный R
|
0,71949
|
|
|
|
|
|
R-квадрат
|
0,51767
|
|
|
|
|
|
Нормированный R-квадрат
|
0,50821
|
|
|
|
|
|
Стандартная ошибка
|
4,41581
|
|
|
|
|
|
Наблюдения
|
53
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
1067,35646
|
1067,35646
|
54,73781
|
1,27887E-09
|
|
Остаток
|
51
|
994,47122
|
19,49943
|
|
|
|
Итого
|
52
|
2061,82768
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Y-пересечение
|
6,515
|
1,14488
|
5,69090
|
6,2289E-07
|
4,21698
|
8,81390
|
Переменная X 1
|
6,702
|
0,90588
|
7,39850
|
1,2789E-09
|
4,88355
|
8,52083
|
Приложение 2.
Расчетная таблица
№ предприятия
|
X1
|
Y
|
Yпр.
|
(Y-Yпр.)
|
Abs((Y-Yпр.)/Y)
|
(Y-Yпр.)2
|
(Xi -Xср.)2
|
1
|
1,23
|
13,26
|
14,7591
|
-1,499
|
0,113
|
2,247
|
0,025
|
2
|
1,04
|
10,16
|
13,4857
|
-3,326
|
0,327
|
11,060
|
0,001
|
3
|
1,8
|
13,72
|
18,5794
|
-4,859
|
0,354
|
23,614
|
0,530
|
4
|
0,43
|
12,85
|
9,39739
|
3,453
|
0,269
|
11,921
|
0,412
|
5
|
0,88
|
10,63
|
12,4134
|
-1,783
|
0,168
|
3,180
|
0,037
|
6
|
0,57
|
9,12
|
10,3357
|
-1,216
|
0,133
|
1,478
|
0,252
|
7
|
1,72
|
25,83
|
18,0432
|
7,787
|
0,301
|
60,634
|
0,420
|
8
|
1,7
|
23,39
|
17,9092
|
5,481
|
0,234
|
30,040
|
0,395
|
9
|
0,84
|
14,68
|
12,1453
|
2,535
|
0,173
|
6,425
|
0,054
|
10
|
0,6
|
10,05
|
10,5368
|
-0,487
|
0,048
|
0,237
|
0,223
|
11
|
0,82
|
13,99
|
12,0112
|
1,979
|
0,141
|
3,915
|
0,063
|
12
|
0,84
|
9,68
|
12,1453
|
-2,465
|
0,255
|
6,078
|
0,054
|
13
|
0,67
|
10,03
|
11,0059
|
-0,976
|
0,097
|
0,952
|
0,162
|
14
|
1,04
|
9,13
|
13,4857
|
-4,356
|
0,477
|
18,972
|
0,001
|
15
|
0,66
|
5,37
|
10,9389
|
-5,569
|
1,037
|
31,013
|
0,170
|
16
|
0,86
|
9,86
|
12,2793
|
-2,419
|
0,245
|
5,853
|
0,045
|
17
|
0,79
|
12,62
|
11,8102
|
0,810
|
0,064
|
0,656
|
0,079
|
18
|
0,34
|
5,02
|
8,79419
|
-3,774
|
0,752
|
14,245
|
0,536
|
19
|
1,6
|
21,18
|
17,2389
|
3,941
|
0,186
|
15,532
|
0,279
|
20
|
1,46
|
25,17
|
16,3006
|
8,869
|
0,352
|
78,665
|
0,151
|
21
|
1,27
|
19,4
|
15,0272
|
4,373
|
0,225
|
19,121
|
0,039
|
22
|
1,58
|
21
|
17,1049
|
3,895
|
0,185
|
15,172
|
0,258
|
23
|
0,68
|
6,57
|
11,0729
|
-4,503
|
0,685
|
20,276
|
0,154
|
24
|
0,86
|
14,19
|
12,2793
|
1,911
|
0,135
|
3,651
|
0,045
|
25
|
1,98
|
15,81
|
19,7858
|
-3,976
|
0,251
|
15,807
|
0,825
|
26
|
0,33
|
5,23
|
8,72717
|
-3,497
|
0,669
|
12,230
|
0,550
|
27
|
0,45
|
7,99
|
9,53143
|
-1,541
|
0,193
|
2,376
|
0,387
|
28
|
0,74
|
17,5
|
11,4751
|
6,025
|
0,344
|
36,300
|
0,110
|
29
|
0,03
|
17,16
|
6,71651
|
10,443
|
0,609
|
109,066
|
1,086
|
30
|
0,99
|
14,54
|
13,1506
|
1,389
|
0,096
|
1,930
|
0,007
|
31
|
0,24
|
6,24
|
8,12397
|
-1,884
|
0,302
|
3,549
|
0,692
|
32
|
0,57
|
12,08
|
10,3357
|
1,744
|
0,144
|
3,043
|
0,252
|
33
|
1,22
|
9,49
|
14,6921
|
-5,202
|
0,548
|
27,062
|
0,022
|
34
|
0,68
|
9,28
|
11,0729
|
-1,793
|
0,193
|
3,215
|
0,154
|
35
|
1
|
11,42
|
13,2176
|
-1,798
|
0,157
|
3,231
|
0,005
|
36
|
0,81
|
10,31
|
11,9442
|
-1,634
|
0,159
|
2,671
|
0,069
|
37
|
1,27
|
8,65
|
15,0272
|
-6,377
|
0,737
|
40,669
|
0,039
|
38
|
1,14
|
10,94
|
14,1559
|
-3,216
|
0,294
|
10,342
|
0,005
|
39
|
1,89
|
9,87
|
19,1826
|
-9,313
|
0,944
|
86,724
|
0,669
|
40
|
0,67
|
6,14
|
11,0059
|
-4,866
|
0,792
|
23,677
|
0,162
|
41
|
0,96
|
12,93
|
12,9495
|
-0,020
|
0,002
|
0,000
|
0,013
|
42
|
0,67
|
9,78
|
11,0059
|
-1,226
|
0,125
|
1,503
|
0,162
|
43
|
0,98
|
13,22
|
13,0836
|
0,136
|
0,010
|
0,019
|
0,008
|
44
|
1,16
|
17,29
|
14,29
|
3,000
|
0,174
|
9,000
|
0,008
|
45
|
0,54
|
7,11
|
10,1346
|
-3,025
|
0,425
|
9,148
|
0,283
|
46
|
1,23
|
22,49
|
14,7591
|
7,731
|
0,344
|
59,766
|
0,025
|
47
|
0,78
|
12,14
|
11,7432
|
0,397
|
0,033
|
0,157
|
0,085
|
48
|
1,16
|
15,25
|
14,29
|
0,960
|
0,063
|
0,922
|
0,008
|
49
|
4,44
|
31,34
|
36,2732
|
-4,933
|
0,157
|
24,336
|
11,344
|
50
|
1,06
|
11,56
|
13,6198
|
-2,060
|
0,178
|
4,243
|
0,000
|
51
|
2,13
|
30,14
|
20,7911
|
9,349
|
0,310
|
87,402
|
1,120
|
52
|
1,21
|
19,71
|
14,6251
|
5,085
|
0,258
|
25,856
|
0,019
|
53
|
2,2
|
23,56
|
21,2603
|
2,300
|
0,098
|
5,289
|
1,273
|
Сумма
|
56,81
|
726,07
|
726,07
|
|
15,569
|
994,471
|
23,762
|
Среднее значение
|
1,0719
|
13,6994
|
13,6994
|
|
0,294
|
18,764
|
|
Х пр./Yпр.
|
1,125
|
14,06
|
|
|
|
|
|
Средняя относительная ошибка аппроксимации
|
29,37%
|
|
|
|
|
|
|
myпр.
|
4,45754
|
|
|
|
|
|
| |
 Скачать 146.77 Kb.
Скачать 146.77 Kb.

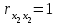


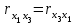




 0,263
0,263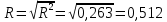
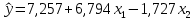
 =28,35
=28,35