КОНТРОЛЬНЫЕ РАБОТЫ ПО МАТСТАТИСТИКЕ_2 СЕМЕСТР (1). Рекомендации по выполнению и оформлению контрольных работ
 Скачать 429.89 Kb. Скачать 429.89 Kb.
|
|
Необходимый объём  повторной выборки: повторной выборки: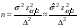 или или 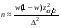 . .Необходимый объём 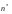 бесповторной выборки: бесповторной выборки: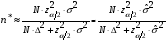 или или 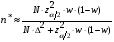 Примечание. Если в формулах для определения необходимого объёма выборки 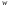 неизвестно, то полагают неизвестно, то полагают 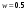 . .Здесь: 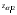 - корень уравнения - корень уравнения 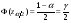 (приложение 2); (приложение 2); 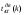 -критическая точка распределения Стьюдента (приложение 4); -критическая точка распределения Стьюдента (приложение 4); 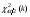 , , 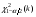 - критические точки распределения - критические точки распределения 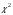 (приложение 3); (приложение 3); 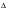 -предельная ошибка выборки; -предельная ошибка выборки; 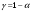 - доверительная вероятность; - доверительная вероятность; 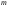 - число элементов в выборке, обладающих данным свойством, - число элементов в выборке, обладающих данным свойством, 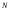 -объём генеральной совокупности. -объём генеральной совокупности.6.3 Проверка параметрических гипотез. Проверка гипотез о средних нормального распределения.
Здесь: 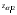 - корень уравнения - корень уравнения 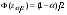 (приложение 2); (приложение 2); 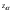 -корень уравнения -корень уравнения 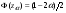 (приложение 2); (приложение 2); 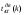 , ,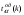 -критические точки распределения Стьюдента для двусторонней и односторонней критической области, соответственно (приложение 4). -критические точки распределения Стьюдента для двусторонней и односторонней критической области, соответственно (приложение 4).Проверка гипотез о дисперсиях нормального распределения.
Здесь: 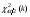 , , 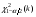 , ,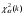 , ,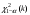 - критические точки распределения - критические точки распределения 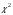 (приложение 3); (приложение 3); 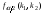 , , 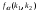 -критические точки распределения Фишера (приложение 5а,б). -критические точки распределения Фишера (приложение 5а,б).Проверка гипотез о параметре 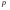 биномиального распределения биномиального распределения
Здесь: 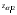 - корень уравнения - корень уравнения 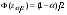 (приложение 2); (приложение 2); 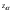 -корень уравнения -корень уравнения 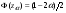 (приложение 2); (приложение 2); 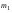 , , 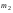 - число элементов в выборках объёма - число элементов в выборках объёма 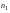 , , 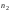 , соответственно, обладающих данным свойством. , соответственно, обладающих данным свойством.Проверка гипотезы о значимости выборочного коэффициента корреляции  . .
Здесь: 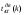 -критическая точка распределения Стьюдента (приложение 4), -критическая точка распределения Стьюдента (приложение 4),  .- объём выборки. .- объём выборки. |

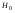
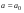
 -известно)
-известно)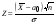
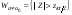
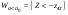
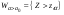
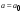
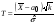 ,
,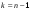
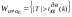
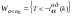
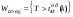
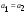
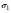 ,
,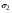 -известны)
-известны)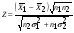
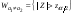
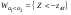
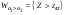
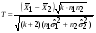
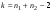
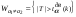
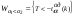
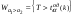
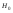
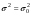
 -неизвестно)
-неизвестно)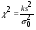 ,
, 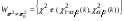
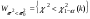
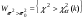
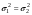
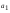 ,
,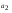 неизвестны)
неизвестны)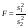 ,
, 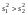
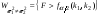 ,
, 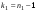 ,
, 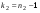
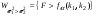 ,
, 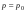
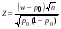 , где
, где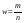
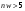 ,
,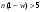 )
)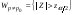
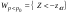
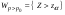
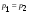
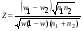 где
где 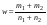
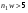 ,
,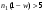 ,
,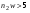 ,
,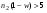 )
)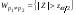
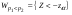
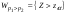
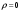
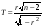
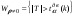 ,
,