КОНТРОЛЬНЫЕ РАБОТЫ ПО МАТСТАТИСТИКЕ_2 СЕМЕСТР (1). Рекомендации по выполнению и оформлению контрольных работ
 Скачать 429.89 Kb. Скачать 429.89 Kb.
|
|
Тема: Корреляционный и регрессионный анализ. ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ ПО РАЗДЕЛУ «МАТЕМАТИЧЕСКАЯ СТАТИСТИКА». I. СТАТИСТИЧЕСКИЕ РЯДЫ. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ВЫБОРКИ. В заданиях 1 – 10 для каждой из приведенных ниже выборок: а) определить размах выборки, построить дискретный статистический ряд и изобразить его графически в виде полигона; б) составить эмпирическую функцию распределения 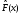 и построить ее график; в) вычислить выборочные: среднее и построить ее график; в) вычислить выборочные: среднее 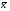 , моду , моду 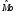 , медиану , медиану 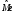 , дисперсию , дисперсию 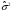 . .Задание 1. Выборка 0 4 2 0 5 1 1 3 0 2 2 4 3 3 3 0 4 5 1 3 1 5 2 0 2 2 2 3 2 2 2 6 2 1 3 1 3 1 5 4 Объем выборки: n = 40. Задание 2. Выборка 23 23 21 20 20 23 23 25 23 20 20 24 21 25 21 25 23 23 20 22 23 21 24 21 22 24 23 24 25 24 Объем выборки: n = 30. Задание 3. Выборка 14 15 16 11 11 16 12 12 17 14 15 15 14 12 13 13 13 14 14 13 17 14 13 15 15 12 11 14 13 15 Объем выборки: n = 30. Задание 4. Выборка 12 12 11 13 14 12 11 11 13 13 14 13 12 14 15 10 14 12 13 14 13 15 11 13 13 13 14 13 12 10 Объем выборки: n = 30. Задание 5. Выборка 19 18 20 16 16 17 19 19 20 14 20 21 21 21 16 21 22 18 17 22 20 19 19 21 21 17 17 21 18 18 Объем выборки: n = 30. Задание 6. Выборка 5 5 4 2 6 2 1 5 3 3 1 5 6 4 3 3 4 1 5 5 3 4 3 7 4 5 6 7 5 2 4 6 6 7 7 3 5 4 4 3 Объем выборки: n = 40. Задание 7. Выборка 22 21 22 23 21 21 20 22 22 24 23 23 20 23 20 22 23 20 22 23 20 22 23 23 24 24 21 24 20 20 Объем выборки: n = 30. Задание 8. Выборка 12 8 11 9 14 11 13 11 9 10 12 13 8 15 10 10 10 11 13 9 13 14 10 12 12 14 10 9 11 11 Объем выборки: n = 30. Задание 9. Выборка 15 10 11 9 12 8 8 9 11 14 15 13 12 10 8 9 11 9 8 13 12 12 12 12 15 12 13 13 9 13 Объем выборки: n = 30. Задание 10. Выборка 1 3 3 2 0 2 4 3 2 1 2 2 2 2 3 3 1 1 1 3 2 1 0 1 2 1 1 4 4 2 3 3 5 5 2 1 2 3 2 3 Объем выборки: n = 40. В заданиях 11 – 20 для каждой из приведенных ниже выборок: а) определить размах выборки, построить интервальный статистический ряд и изобразить его графически в виде гистограммы и кумуляты; б) вычислить выборочные: среднее 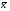 , моду , моду 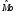 , медиану , медиану 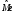 , дисперсию , дисперсию 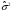 . . Задание 11. Выборка 65 72 85 89 95 103 64 72 85 91 96 105 64 77 82 91 101 104 110 101 91 80 71 62 68 74 85 87 95 98 93 85 75 63 73 82 87 100 95 89 83 73 85 87 95 87 83 92 92 88. Объем выборки: n = 50. Первый интервал: 62 – 70. Задание 12. Выборка 48 53 58 61 65 69 76 75 70 66 62 59 54 49 50 55 57 61 67 71 67 63 58 55 50 51 53 58 62 61 59 54 51 49 54 57 58 55 50 51 49 54 53 50 50 54 53 55 55 58. Объем выборки: n = 50. Первый интервал: 48 – 52. Задание 13. Выборка 10,0 13,0 15,4 17,0 19,0 21,0 23,0 22,2 21,0 18,1 16,2 15,6 12,8 11,0 13,1 14,2 16,4 18,5 20,4 24,0 21,5 19,5 16,5 14,4 15,7 17,0 19,8 20,3 15,0 20,1 18,2 21,0 18,2 16,2 19,6 21,4 18,4 16,8 14,7 14,8 17,0 17,0 19,2 21,6 20,2 18,4 19,4 20,3 19,0 19,1. Объем выборки: n = 50. Первый интервал: 10 – 12. Задание 14. Выборка 21 33 38 51 60 68 14 28 41 45 60 74 57 72 53 42 32 30 42 52 67 55 59 65 47 35 30 58 46 41 49 58 40 49 39 61 61 47 43 55 48 42 47 60 45 45 55 59 48 50. Объем выборки: n = 50. Первый интервал: 14 – 24. Задание 15. Выборка 38 46 54 57 64 69 69 65 61 55 51 42 41 51 55 57 63 74 65 58 54 46 43 40 47 51 57 64 64 59 54 48 48 42 51 51 57 57 57 55 45 46 47 55 59 59 52 49 55 51. Объем выборки: n = 50. Первый интервал: 38 – 44. Задание 16. Выборка 14 21 28 34 40 50 46 46 40 35 28 22 15 16 24 30 36 40 41 35 30 25 17 15 25 25 18 31 30 34 33 30 24 19 18 22 28 23 16 16 22 21 21 15 16 22 24 24 25 21. Объем выборки: n = 50. Первый интервал: 14 – 20. Задание 17. Выборка 26 33 39 48 55 62 27 34 40 49 51 57 30 35 41 48 52 60 60 52 48 41 35 30 29 33 39 47 54 61 62 55 48 42 35 28 36 42 48 51 52 48 42 36 43 45 46 40 48 49. Объем выборки: n = 50. Первый интервал: 26 – 32. Задание 18. Выборка 8,8 11,7 13,4 14,7 17,0 18,8 18,1 17,9 15,2 13,0 11,6 8,0 9,3 11,3 13,9 15,1 16,5 20,0 18,3 16,6 15,1 12,4 10,7 10,1 13,7 14,2 16,4 17,6 14,6 12,3 15,8 14,7 15,8 14,6 17,6 17,2 15,1 13,8 13,5 14,1 16,3 16,2 14,5 12,7 13,5 15,5 16,9 16,1 17,7 15,7. Объем выборки: n = 50. Первый интервал: 8 – 10. Задание 19. Выборка 25 31 48 58 66 72 80 64 53 49 32 20 20 33 46 59 61 84 85 65 55 42 35 36 44 56 66 71 68 55 45 46 55 69 66 54 45 53 66 62 54 52 64 68 51 52 68 68 67 65. Объем выборки: n = 50. Первый интервал: 20 – 30. Задание 20. Выборка 20 26 31 40 44 51 56 55 50 45 38 32 25 18 22 26 33 40 46 52 57 58 49 45 40 34 27 21 28 35 37 47 50 59 58 53 43 38 32 39 43 50 55 50 44 45 52 53 49 50. Объем выборки: n = 50. Первый интервал: 18 – 24. II. ИНТЕРВАЛЬНЫЕ ОЦЕНКИ. В заданиях 21 – 30, в предположении, что выборки получены из нормально распределённых генеральных совокуп-ностей, требуется найти 95%-ные доверительные интервалы: а) для генерального среднего; б) для генерального среднего квадратичного отклонения. Задание 21. Результаты измерений твёрдости 12 образцов легированной стали (в условных единицах): 13.0 12.8 12.0 13.5 13.7 13.8 10.6 12.4 13.5 11.8 14.0 12.5 Задание 22. Данные о часовой выработке (в ед/ч) 50 рабочих механического цеха завода: Часовая выработка 0.9 1.1 1.3 1.5 1.7 1.9 Число рабочих 1 2 10 17 16 4 Задание 23. Данные о скорости 10 автомобилей в некоторой точке трассы (в км/ч): 70 85 63 54 65 80 75 95 52 55 Задание 24. Данные хронометража операции пайки 35 радиаторов (в мин.) на ремонтном предприятии: Время пайки, мин 20–30 30–40 40–50 50–60 60–70 Кол-во радиаторов 2 5 10 17 1 Задание 25. Данные о производительности механического цеха завода (в условных единицах) в течение 12 рабочих дней: 13.0 13.1 13.0 12.5 12.8 12.3 12.1 12.2 12.1 12.7 12.0 12.6 Задание 26. Данные о пробеге 120 автомобильных шин (в тыс. км), эксплуатируемых в городских условиях: Пробег шин, тыс.км 40–42 42–44 44–46 46–48 48–50 50-52 Число шин 4 8 22 36 30 20 Задание 27. Данные о возрастном составе студентов заочного отделения одного из факультетов КамПИ: 22 23 35 33 27 29 24 30 32 28 25 26 Задание 28. Данные о длине межремонтного пробега (в тыс. км) 100 автомобилей “КамаЗ – 5320”: Величина межремонтного пробега,тыс.км- 80–100 100–120 120–140 140–160 Число автомобилей 14 30 40 16 Задание 29. Данные об интенсивности движения автомобилей (авт./час) на одном из участков автомагистрали Набережные Челны – Казань: 140 110 80 140 210 220 90 150 120 130. Задание 30. Результаты измерений процента влажности древесины, из которой изготовлены 150 изделий, случайным образом отобранных из большой партии изделий: Процент влажности 11–13 13–15 15–17 17–19 19–21 Число изделий 8 42 51 37 12 Задание 31. Из большой партии транзисторов одного типа были случайным образом отобраны и проверены 100 штук. У 36 транзисторов коэффициент усиления оказался меньше 10. Найти 95%-ный доверительный интервал для доли таких транзисторов во всей партии. Задание 32. При осмотре 60 ящиков обнаружено 10 поврежденных. Найти 95%-ный доверительный интервал для доли поврежденных ящиков во всей партии. Задание 33. Из 150 однотипных электронных ламп 30 ламп вышли из строя после 1000 часов работы из-за обрыва нити накала. Найти 95%-ный доверительный интервал для доли таких ламп в большой партии ламп этого типа. Задание 34. Среди 250 деталей, изготовленных станком-автоматом, оказалось 32 нестандартных. Найти 95%-ный доверительный интервал для вероятности изготовления станком-автоматом нестандартной детали. Задание 35. В процессе технического контроля из большой партии готовой продукции было проверено 70 изделий, из которых 4 оказались бракованными. Найти 95%-ный доверительный интервал для доли бракованных изделий во всей партии. Задание 36. В 10 000 сеансах игры с автоматом выигрыш появился 4 000 раз. Найти 95%-ный доверительный интервал для вероятности выигрыша. Задание 37. С автоматической линии, производящей подшипники, было отобрано 400 штук, причем 10 оказались бракованными. Найти 95%-ный доверительный интервал для вероятности изготовления бракованного подшипника. Задание 38. Было обследовано 150 студентов дневного отделения одного из высших учебных заведений. Доля студентов, совмещающих работу и учёбу, составила, по данным выборки, 30%. Найти 95%-ный доверительный интервал для доли студентов дневного отделения этого учебного заведения, работающих в течение учебного года. Задание 39. При отгрузке партии картофеля было проверено 600 клубней, из которых 36 не соответствовали стандарту. Найти 95%-ный доверительный интервал для доли клубней, удовлетворяющих стандарту, во всей партии. Задание 40. В ходе аудиторской проверки фирмы была проведена случайная выборка записей по счетам. Из выборки в 200 записей 10 содержали некоторые ошибки. Найти 95%-ный доверительный интервал для доли ошибок во всей генеральной совокупности записей. III. ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ. ПРЕДЕЛЬНАЯ ОШИБКА И НЕОБХОДИМЫЙ ОБЪЁМ ВЫБОРКИ. Задание 41. Предполагается, что в лесном массиве 1000 животных одного вида. Найти объёмы повторной и бесповторной выборок, образуемых для определения доли заболевших животных, если доверительная вероятность равна 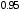 , а предельная ошибка выборки не должна превышать 5%. , а предельная ошибка выборки не должна превышать 5%. Задание 42. Найти объёмы повторной и бесповторной выборок из 5000 автомобилей для определения среднего пробега без ремонта, чтобы с доверительной вероятностью 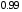 предельная ошибка выборки не превосходила 25 тыс. км. Генеральное среднее квадратичное отклонение принять равным 150 тыс. км. предельная ошибка выборки не превосходила 25 тыс. км. Генеральное среднее квадратичное отклонение принять равным 150 тыс. км.Задание 43. Из партии, содержащей 5000 изделий, проверено 400. Среди них оказалось 300 изделий высшего сорта. Найти доверительную вероятность того, что доля изделий высшего сорта во всей партии отличается по абсолютной величине от доли их в выборке не более чем на 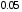 . Рассмотреть случаи повторной и бесповторной выборок. . Рассмотреть случаи повторной и бесповторной выборок.Задание 44. На склад поступило 8000 банок тушёнки. Какими должны быть объёмы повторной и бесповторной выбо-рок, чтобы с доверительной вероятностью  можно было утверждать, что доли удовлетворяющих стандарту банок в выборке и генеральной совокупности различаются по абсо-лютной величине не более чем на можно было утверждать, что доли удовлетворяющих стандарту банок в выборке и генеральной совокупности различаются по абсо-лютной величине не более чем на  . .Задание 45. Найти необходимые объёмы повторной и бесповторной выборок среди 8000 призывников района для определения доли призывников годных к службе в армии, если доверительная вероятность равна  , а предельная ошибка выборки не должна превышать , а предельная ошибка выборки не должна превышать  . .Задание 46. Определить необходимые объёмы повторной и бесповторной выборок, чтобы при определении средней продолжительности горения лампочек, в партии из 5000 лампочек,с доверительной вероятностью  отклонение генеральной средней от выборочной средней не превосходило по абсолютной величине 25 часов. Генеральное среднее квадратичное отклонение принять равным 150 часам. отклонение генеральной средней от выборочной средней не превосходило по абсолютной величине 25 часов. Генеральное среднее квадратичное отклонение принять равным 150 часам.Задание 47. Для выяснения всхожести семян в партии из 800 штук было отобрано 500, из которых взошло 440. Найти доверительную вероятность того, что доля всхожих семян во всей партии отличается по абсолютной величине от доли их в выборке не более чем на  . Рассмотреть случаи повторной и бесповторной выборок. . Рассмотреть случаи повторной и бесповторной выборок.Задание 48. Из 5000 вкладчиков банка было отобрано 300. Средний размер вклада в выборке составил 8000 руб., а среднее квадратичное отклонение 2500 руб. Какова доверительная веро-ятность того, что средний размер вклада случайно выбранного вкладчика отличается по абсолютной величине от его среднего размера в выборке не более чем на 100 руб. Рассмотреть случаи повторной и бесповторной выборок. Задание 49. На фабрике работает 2000 ткачих. Найти объёмы повторной и бесповторной выборок, для определения средней дневной выработки ткачих с точностью до  м и гарантировать полученный результат с доверительной вероятностью м и гарантировать полученный результат с доверительной вероятностью  , если известно, что среднее квадратичное отклонение дневной выработки ткачих составляет , если известно, что среднее квадратичное отклонение дневной выработки ткачих составляет 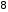 м. м.Задание 50. Из поступивших на инкубаторную станцию 40000 яиц была образована выборочная совокупность из 400 яиц. Из них вывелось 304 цыплёнка. Найти доверительную вероятность того, что во всей совокупности удельный вес яиц, из которых выведутся цыплята, отличается по абсолютной величине от удельного веса их в выборке не более чем на 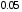 . Рассмотреть случаи повторной и бесповторной выборок. . Рассмотреть случаи повторной и бесповторной выборок.IV. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ О ПАРАМЕТРАХ РАСПРЕДЕЛЕНИЙ. Задание 51. Партия изделий принимается в том случае, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 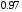 . Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости . Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости 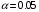 принять партию изделий? принять партию изделий?Задание 52. В соответствии с техническими условиями среднее время безотказной работы для приборов из большой партии должно составлять не менее 1000 часов. Для случайно отобранных 25 приборов, выборочное среднее времени безотказной работы  часов, а выборочное среднее квадратичное отклонение часов, а выборочное среднее квадратичное отклонение  часов. Можно ли на уровне значимости часов. Можно ли на уровне значимости  считать, что вся партия приборов не удовлетворяет техническим условиям? считать, что вся партия приборов не удовлетворяет техническим условиям?Задание 53. Предельная сила натяжения прядильной нити в среднем равна 20 г. Выборку нити из 64 мотков обработали некоторым химическим составом. После просушки была заново измерена предельная сила натяжения нити. В среднем она оказалась равной 21 г. Предполагая, что выборочное среднее квадратичное отклонение предельной силы натяжения нити  г до и после обработки, проверить на уровне значимости г до и после обработки, проверить на уровне значимости 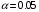 гипотезу о том, что эта обработка не увеличила предельной силы натяжения нити. гипотезу о том, что эта обработка не увеличила предельной силы натяжения нити.Задание 54. Из большой партии резисторов одного типа и номинала случайным образом отобраны 36 штук. При этом оказалось, что выборочное среднее величины сопротивления 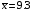 кОм, а выборочное среднее квадратичное отклонение кОм, а выборочное среднее квадратичное отклонение 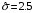 кОм. На уровне значимости кОм. На уровне значимости 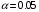 проверить гипотезу о том, что выборка взята из партии с номиналом проверить гипотезу о том, что выборка взята из партии с номиналом 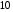 кОм. кОм.Задание 55. По техническим условиям средняя прочность на разрыв троса составляет 2000 кг. В результате испытаний 20 кусков троса было установлено, что средняя прочность на разрыв 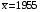 кг при выборочном среднем квадратичном отклонении кг при выборочном среднем квадратичном отклонении 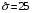 кг. На уровне значимости кг. На уровне значимости 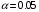 выяснить удовлетворяет ли образец троса техническим условиям. выяснить удовлетворяет ли образец троса техническим условиям.Задание 56. Количество бракованных деталей в партии не должно превышать 5%. В результате контроля 100 деталей из этой партии обнаружено шесть бракованных. Можно ли на уровне значимости 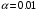 считать, что процент брака превосходит допустимый? считать, что процент брака превосходит допустимый? |
