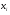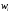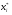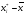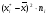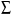КОНТРОЛЬНЫЕ РАБОТЫ ПО МАТСТАТИСТИКЕ_2 СЕМЕСТР (1). Рекомендации по выполнению и оформлению контрольных работ
 Скачать 429.89 Kb. Скачать 429.89 Kb.
|
|
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ. Прежде чем выполнять контрольные работы, следует изучить теоретический материал по указанной литературе и ответить на вопросы для самоподготовки. При выполнении контрольных работ необходимо придерживаться указанных ниже правил: Контрольная работа должна быть выполнена студентом в отдельной ученической тетради с полями не менее 3 см для замечаний преподавателя. На обложке тетради указывается фамилия,имя,отчество студента, номер группы, курс, факультет и специальность, по которой студент обучается. Условие задачи переписывается полностью, без сокращения слов, после чего приводится подробное решение (чертежи можно выполнять аккуратно от руки). В конце решения приводится ответ. В работу должны быть включены все задачи, указанные в задании, строго по варианту. Контрольные работы, содержащие не все задания, а также задачи не своего варианта, не зачитываются. ТАБЛИЦА НОМЕРОВ ВЫПОЛНЯЕМЫХ ЗАДАНИЙ №варианта НОМЕРА ВЫПОЛНЯЕМЫХ ЗАДАНИЙ 1 1, 11, 21, 31, 41, 51, 61, 71, 2 2, 12, 22, 32, 42, 52, 62, 72 3 3, 13, 23, 33, 43, 53, 63, 73 4 4, 14, 24, 34, 44, 54, 64, 74 5 5, 15, 25, 35, 45, 55, 65, 75 6 6, 16, 26, 36, 46, 56, 66, 76 7 7, 17, 27, 37, 47, 57, 67, 77 8 8, 18, 28, 38, 48, 58, 68, 78 9 9, 19, 29, 39, 49, 59, 69, 79 10 10, 20, 30, 40, 50, 60, 70, 80, 11 3, 12, 21, 32, 43, 52, 61, 72, 12 4, 13, 22, 33, 44, 53, 62, 73, 13 5, 16, 27, 38, 49, 60, 69, 78, 14 6, 17, 28, 39, 50, 59, 68, 77, 15 7, 18, 29, 40, 49, 58, 67, 76, 16 8, 19, 30, 39, 48, 57, 66, 75, 17 9, 20, 29, 38, 47, 56, 65, 74, 18 1, 12, 23, 34, 45, 56, 67, 78 19 2, 13, 24, 35, 46, 57, 68, 79, 20 3, 14, 25, 36, 47, 58, 69, 80, 21 4, 15, 26, 37, 48, 59, 70, 79, 22 5, 14, 23, 32, 41, 52, 63, 74, 23 6, 15, 24, 33, 42, 51, 62, 73, 24 7, 16, 25, 34, 43, 52, 61, 72, 25 8, 17, 26, 35, 44, 53, 62, 71, 26 9, 18, 27, 36, 45, 54, 63, 72, 27 10, 19, 28, 37, 46, 55, 64, 73, 28 2, 11, 22, 33, 44, 55, 66, 77, 29 3, 12, 21, 32, 43, 54, 65, 76, 30 4, 13, 22, 31, 42, 53, 64, 75, ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Математическая статистика. Тема: Вариационные ряды и их характеристики. Пример. По данной выборке (N=41):
Элементы выборки:
Решение. 1. Для построения дискретного ряда распределения располагаем различные значения признака Х в порядке их возрастания и для каждого из этих значений определяем его частоту, а также относительную частоту (частость 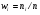 ). Результаты группировки сводим в таблицу. Кроме перечисленных характеристик вычисляем накопленные частоты: ). Результаты группировки сводим в таблицу. Кроме перечисленных характеристик вычисляем накопленные частоты:
2. Построим полигон частот: 3. Определим статистические показатели ряда распределения. Среднее арифметическое признака Х определяется по формуле: 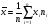 , где , где 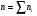 - объем вариационного ряда. - объем вариационного ряда.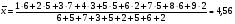 Выборочная дисперсия признака определяется по формуле: 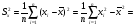 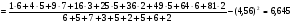 Среднеквадратическое отклонение признака Х определяется по формуле: 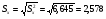 . .Тема: Проверка статистических гипотез. Пример. По заданной выборке проверить гипотезу о нормальном распределении СВ по критерию согласия Пирсона. Произвести интервальную оценку выборочного среднего значения с доверительной вероятностью 0,98. n=182
Решение. Для построения интервального ряда распределения определим число групп в ряду распределения по формуле Г.А.Стерджесса: 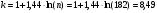 . .Принимаем число интервалов 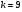 . .Максимальное значение ряда 103, минимальное значение ряда 55. Длина интервала: 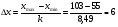 . .Центр распределения: 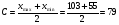 . .Поскольку число интервалов нечетное, центр распределения находится в центре среднего интервала. Полученный ряд распределения: (52-58); (58-64); (64-70); (70-76); (76-82); (82-88); (88-94); (94-100); (100-106). Принимаем гипотезу 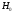 , утверждающую, что случайная величина Х имеет нормальный закон распределения. В качестве критерия для проверки этой гипотезы используем случайную величину , утверждающую, что случайная величина Х имеет нормальный закон распределения. В качестве критерия для проверки этой гипотезы используем случайную величину 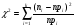 -критерий согласия Пирсона, который имеет приближенное распределение с числом степеней свободы -критерий согласия Пирсона, который имеет приближенное распределение с числом степеней свободы 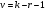 . Здесь k – число интервалов, на которые разделена область изменения Х; r – количество неизвестных параметров теоретического распределения , оценки которых вычисляются по выборке; n – объем выборки; . Здесь k – число интервалов, на которые разделена область изменения Х; r – количество неизвестных параметров теоретического распределения , оценки которых вычисляются по выборке; n – объем выборки; 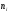 - эмпирические частоты; - эмпирические частоты; 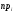 - теоретические частоты, где - теоретические частоты, где 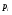 - вероятность попадания значения признака Х в i-й интервал. Чтобы утверждение о распределении случайной величины по закону - вероятность попадания значения признака Х в i-й интервал. Чтобы утверждение о распределении случайной величины по закону 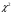 было достаточно точным, требуется выполнение условия было достаточно точным, требуется выполнение условия 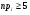 . В случае невыполнения условия для некоторых интервалов, их объединяют с соседними. . В случае невыполнения условия для некоторых интервалов, их объединяют с соседними.Теоретические частоты вычислим по формулам: 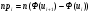 , где , где 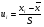 , , 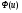 - значения функции распределения нормированного нормального распределения (находится по таблице). - значения функции распределения нормированного нормального распределения (находится по таблице).Внимание! Если в таблице значений функции 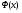 пределы интегрирования от 0 до х, т.е. пределы интегрирования от 0 до х, т.е.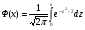 , то , то 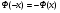 , , 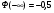 , , 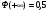 Если в таблице значений функции 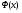 пределы интегрирования от - до х, т.е. пределы интегрирования от - до х, т.е.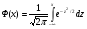 , то , то 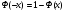 , , 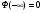 , , 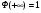 . .Левый конец первого интервала принимаем равным -, а правый конец последнего интервала +. Определим эмпирические частоты и характеристики выборки:
Характеристики выборки рассчитываются по следующим формулам: Выборочное среднее 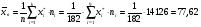 Выборочная дисперсия 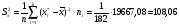 Среднеквадратическое отклонение 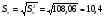 . .Определим доверительный интервал для 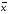 . Интервальной оценкой (с надежностью γ) математического ожидания а нормально распределенного количественного признака Х по выборочной средней . Интервальной оценкой (с надежностью γ) математического ожидания а нормально распределенного количественного признака Х по выборочной средней 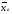 при неизвестном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал при неизвестном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал 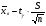 < a < < a <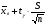 , где S – «исправленное» выборочное среднее квадратическое отклонение ( , где S – «исправленное» выборочное среднее квадратическое отклонение (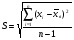 ), ), 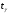 находят по таблице критических точек распределения Стьюдента по заданному числу степеней свободы находят по таблице критических точек распределения Стьюдента по заданному числу степеней свободы 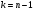 и уровню значимости и уровню значимости 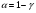 . Для γ = 0,98 и n = 182 . Для γ = 0,98 и n = 182 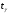 =2,33. =2,33. 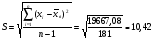 , ,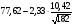 < a < < a <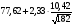 . .Таким образом, интервалом, покрывающим 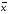 с вероятностью 0,98, служит интервал (75,82; 79,42). с вероятностью 0,98, служит интервал (75,82; 79,42).Для вычисления теоретических характеристик составим расчетную таблицу.
Поскольку для последнего интервала теоретическая частота меньше 5, объединим два последних интервала в один и на основании полученных величин найдем расчетное значение критерия Пирсона.
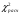 =2,44. =2,44. Для определения критического значения критерия Пирсона найдем число степеней свободы 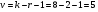 . Здесь k – число групп ряда распределения в последней таблице; r – число параметров нормального закона распределения, оценки которых вычислялись по выборке. . Здесь k – число групп ряда распределения в последней таблице; r – число параметров нормального закона распределения, оценки которых вычислялись по выборке.По таблице критических точек распределения 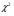 для уровня значимости 0,02 и числа степеней свободы 5 находим для уровня значимости 0,02 и числа степеней свободы 5 находим 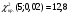 . .Поскольку 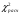 < <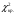 , то значение , то значение 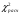 не принадлежит критической области и, следовательно, гипотеза о нормальном распределении генеральной совокупности Х принимается. не принадлежит критической области и, следовательно, гипотеза о нормальном распределении генеральной совокупности Х принимается. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||