КОНТРОЛЬНЫЕ РАБОТЫ ПО МАТСТАТИСТИКЕ_2 СЕМЕСТР (1). Рекомендации по выполнению и оформлению контрольных работ
 Скачать 429.89 Kb. Скачать 429.89 Kb.
|
|
Задание 57. Установлено, что средний вес таблетки лекарства сильного действия (номинал) должен быть равен 0.5 мг. Выборочная проверка 100 таблеток показала, что средний вес таблетки 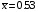 мг, а выборочное среднее квадратичное отклонение мг, а выборочное среднее квадратичное отклонение 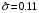 мг. На уровне значимости мг. На уровне значимости 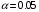 выяснить, можно ли считать полученное в выборке отклонение от номинала случайным? выяснить, можно ли считать полученное в выборке отклонение от номинала случайным? Задание 58. Фирма рассылает рекламные каталоги возможным заказчикам. Как показывает опыт, вероятность того, что организация, получившая каталог, закажет рекламируемое изделие, равна 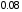 . Фирма разослала 1000 каталогов новой улучшенной формы и получила 100 заказов. Выяснить на уровне значимости . Фирма разослала 1000 каталогов новой улучшенной формы и получила 100 заказов. Выяснить на уровне значимости 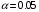 можно ли считать, что новая форма рекламы существенно лучше прежней? можно ли считать, что новая форма рекламы существенно лучше прежней?Задание 59. Фирма, производящая электрические лампочки, утверждает, что среднее время безотказной работы лампочек по меньшей мере 800 часов. Из некоторой большой партии лампочек произведена выборка 25 лампочек, для которой выборочное среднее времени работы лампочек 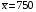 часов, а выборочное среднее квадратичное отклонение часов, а выборочное среднее квадратичное отклонение 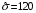 часов. Можно ли на основании этого сказать, что исследуемая выборка лампочек не удовлетворяет гарантии? Уровень значимости принять равным часов. Можно ли на основании этого сказать, что исследуемая выборка лампочек не удовлетворяет гарантии? Уровень значимости принять равным 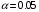 . .Задание 60. Производители нового типа аспирина утверждают, что он снимает головную боль за 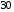 мин. Случайная выборка 100 человек, страдающих головными болями, показала, что новый тип аспирина снимает головную боль за мин. Случайная выборка 100 человек, страдающих головными болями, показала, что новый тип аспирина снимает головную боль за 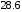 мин при среднем квадратичном отклонении мин при среднем квадратичном отклонении 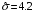 мин. Проверьте на уровне значимости мин. Проверьте на уровне значимости 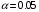 справедливость утверждения производителей аспирина о том, что это лекарство излечивает головную боль за справедливость утверждения производителей аспирина о том, что это лекарство излечивает головную боль за 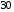 мин. мин.Задание 61. При исследовании стабилизатора напряжения самолёта на стенде проведено 9 независимых испытаний и получена оценка дисперсии выходного напряжения 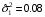 В2. В полёте проведено ещё 15 испытаний, в резу-льтате которых оценка дисперсии выходного напряжения ока-залась равной В2. В полёте проведено ещё 15 испытаний, в резу-льтате которых оценка дисперсии выходного напряжения ока-залась равной 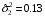 В2. Есть ли основания полагать, что факторы, воздействующие на стабилизатор в полёте, оказывают существенное влияние на его точность? Уровень значимости принять равным В2. Есть ли основания полагать, что факторы, воздействующие на стабилизатор в полёте, оказывают существенное влияние на его точность? Уровень значимости принять равным 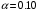 . .Задание 62. Ожидается, что добавление специальных веществ уменьшает жёсткость воды. Оценки жёсткости воды до и после добавления специальных веществ по 40 и 50 пробам соответственно показали средние значения жёсткости (в градусах жёсткости), равные 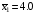 и и 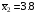 градуса. Гене-ральная дисперсия измерений в обоих случаях предполагается известной и равной градуса. Гене-ральная дисперсия измерений в обоих случаях предполагается известной и равной 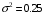 град2. Выяснить на уровне значимости град2. Выяснить на уровне значимости 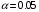 подтверждают ли эти результаты ожидаемый эффект? подтверждают ли эти результаты ожидаемый эффект?Задание 63. Предполагается, что применение новой технологии в производстве микросхем приведёт к увеличению выхода годной продукции. Результаты контроля двух партий продукции, изготовленных по старой и новой технологии, приведены ниже:  Подтверждают ли на уровне значимости 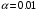 эти результаты предположение об увеличении выхода годной продукции? эти результаты предположение об увеличении выхода годной продукции?Задание 64. Два пресса штампуют детали одного наименования. Из партии деталей, изготовленных первым прессом, проверено 1000 деталей, из которых 25 оказались негодными. Из 800 деталей, изготовленных вторым прессом, негодными оказались 36 деталей. Согласуются ли эти результаты с предположением о равенстве доли брака в продукции двух прессов на уровне значимости 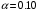 ? ?Задание 65. Вступительный экзамен по математике проводился на двух факультетах института. На машиностроительном факультете из 900 абитуриентов выдержали экзамен 500 человек, а на автомеханическом из 800 абитуриентов выдержали экзамен 408 человек. На уровне значимости 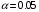 проверить гипотезу об отсутствии существенных различий в уровне подготовки абитуриентов двух факультетов. проверить гипотезу об отсутствии существенных различий в уровне подготовки абитуриентов двух факультетов. Задание 66. До наладки станка была проверена точность изготовления 10 втулок и найдено значение оценки дисперсии диаметра 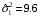 мкм2. После наладки подверглись выбороч-ному контролю ещё 15 втулок и получено новое значение оцен-ки дисперсии мкм2. После наладки подверглись выбороч-ному контролю ещё 15 втулок и получено новое значение оцен-ки дисперсии 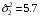 мкм2. Можно ли на уровне значимости мкм2. Можно ли на уровне значимости 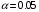 считать, что в результате наладки станка точность изготовления деталей увеличилась? считать, что в результате наладки станка точность изготовления деталей увеличилась?Задание 67. Было произведено 12 измерений диаметра вала. При этом оказалось, что выборочное среднее 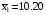 мм, а выборочная дисперсия мм, а выборочная дисперсия 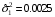 мм2. Затем вал поместили в условия с высокой температурой и произвели ещё 8 измерений его диаметра. Выборочное среднее на этот раз оказалось равным мм2. Затем вал поместили в условия с высокой температурой и произвели ещё 8 измерений его диаметра. Выборочное среднее на этот раз оказалось равным 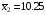 мм, а выборочная дисперсия мм, а выборочная дисперсия 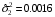 мм2. Предполагается, что генеральные дисперсии мм2. Предполагается, что генеральные дисперсии 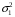 и и 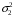 неизвестны, но равны. Выяснить на уровне значимости неизвестны, но равны. Выяснить на уровне значимости 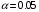 можно ли сделать вывод, что диаметр вала существенно увеличивается в условиях высокой температуры. можно ли сделать вывод, что диаметр вала существенно увеличивается в условиях высокой температуры.Задание 68. Два штурмана определили пеленг маяка по нескольким замерам, используя различные пеленгаторы. Результаты замеров: 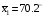 при при 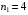 и и 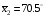 при при 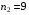 . На уровне значимости . На уровне значимости 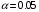 , проверить гипотезу о том, что различие результатов вызвано только случайными ошибками если генеральные средние квадратичные отклонения для обоих пеленгаторов известны и равны: , проверить гипотезу о том, что различие результатов вызвано только случайными ошибками если генеральные средние квадратичные отклонения для обоих пеленгаторов известны и равны: 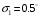 и и 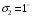 . .Задание 69. Для изучения эффективности профилактического лекарства против аллергии обследовалось две группы людей, предрасположенных к этому заболеванию. Результаты обследования следующие:  Выяснить на уровне значимости 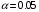 показывают ли эти результаты эффективность лекарства? показывают ли эти результаты эффективность лекарства?Задание 70. Два токарных станка-автомата изготовляют детали по одному чертежу. Из продукции первого станка было отобрано 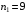 деталей, а из продукции второго деталей, а из продукции второго 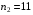 деталей. Выборочные дисперсии контрольного размера, опреде-лённые по этим выборкам: деталей. Выборочные дисперсии контрольного размера, опреде-лённые по этим выборкам: 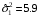 мкм2 и мкм2 и 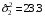 мкм2. Проверить на уровне значимости мкм2. Проверить на уровне значимости 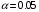 гипотезу о равенстве дисперсий, если альтернативная гипотеза утверждает, что дисперсия размера для второго станка больше, чем для первого. гипотезу о равенстве дисперсий, если альтернативная гипотеза утверждает, что дисперсия размера для второго станка больше, чем для первого.V. ПРОВЕРКА ГИПОТЕЗЫ О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ. В заданиях 71 – 80 для каждой из приведенных ниже группированных случайных выборок: а) проверить, используя критерий 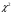 , при уровне значимости , при уровне значимости 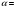 0.05, гипотезу о том, что они получены из нормально распределенных генеральных совокупностей; б) построить на одном чертеже гистограмму эмпирического распределения и нормальную кривую соответствующего теоретического распределения. 0.05, гипотезу о том, что они получены из нормально распределенных генеральных совокупностей; б) построить на одном чертеже гистограмму эмпирического распределения и нормальную кривую соответствующего теоретического распределения.Задание 71. Результаты измерений роста (в см) 100 студентов: Середины интервалов 162 166 170 174 178 182 186 Частоты 10 14 26 28 12 8 2 Задание 72. Результаты измерений внутреннего диаметра (в мкм) 150 поршневых колец: Середины интервалов 29 31 33 35 37 39 41 43 45 Частоты 1 13 17 22 30 31 17 15 4 Задание 73. Данные о расходах фирмы на рекламу (в % к общим расходам фирмы) для 1000 фирм, участвовавших в международной выставке: Середины интервалов 0.75 1.25 1.75 2.25 2.75 3.25 3.75 4.25 Частоты 46 123 525 228 35 28 12 3 Задание 74. Данные о товарообороте (в млн. руб.) 140 продовольственных магазинов города: Середины интервалов 45 55 65 75 85 95 105 115 125 Частоты 6 9 20 38 26 21 14 5 1 Задание 75. Данные о содержании меди (в %) в 500 образцах сплава: Середины интервалов 57 59 61 63 65 67 69 71 73 Частоты 5 29 63 116 117 102 48 14 6 Задание 76. Результаты измерений входного сопротивления (в Ом) 130 электронных ламп: Середины интервалов 3.3 3.9 4.5 5.1 5.7 6.3 6.9 Частоты 2 8 35 40 25 15 5 Задание 77. Данные о среднем годовом надое (в тыс. л) для 200 коров: Середины интервалов 3 4 5 6 7 8 Частоты 10 26 56 64 30 14 Задание 78. Данные о содержании деловой древесины в одном дереве (в куб. м) для 150 деревьев: Середины интервалов 0.3 0.5 0.7 0.9 1.1 1.3 1.5 1.7 Частоты 9 15 29 35 32 19 8 3 Задание 79. Результаты наблюдений за среднесуточной температурой воздуха (в С) в течение 300 суток: Середины интервалов -35 -25 -15 -5 5 15 25 35 Частоты 6 18 47 80 89 40 16 4 Задание 80. Результаты измерений отклонений диаметров (в мкм) 120 валиков, обработанных на станке, от заданного размера: Середины интервалов ПРИЛОЖЕНИЕ_1'>-17.5 -12.5 -7.5 -2.5 2.5 7.5 12.5 17.5 22.5 Частоты 4 8 15 18 26 19 14 10 6 ПРИЛОЖЕНИЯ. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ И ФОРМУЛЫ. ПРИЛОЖЕНИЕ 1 Таблица значений функции 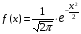 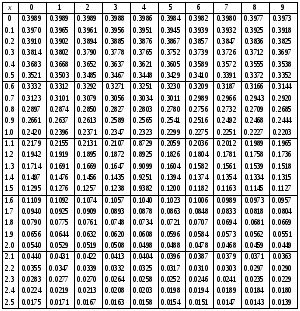 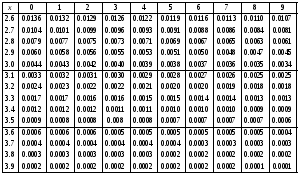 ПРИЛОЖЕНИЕ 2 Таблица значений функции 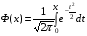 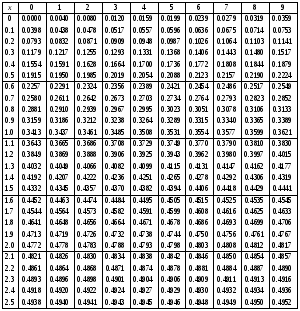 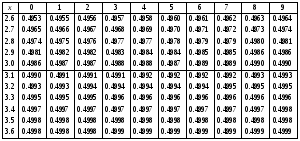 ПРИЛОЖЕНИЕ 3 Критические точки распределения 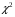 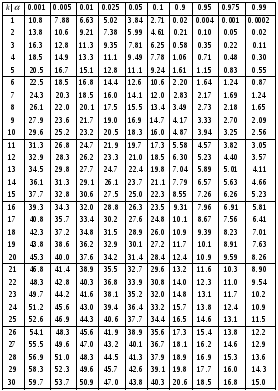 ПРИЛОЖЕНИЕ 4 Критические точки распределения Стьюдента 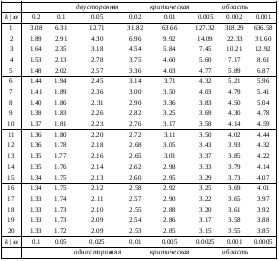 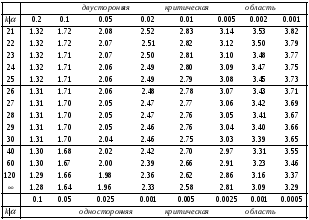 ПРИЛОЖЕНИЕ 5.1 Критические точки распределения Фишера 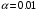 ( 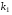 -число степеней свободы большей дисперсии, -число степеней свободы большей дисперсии, 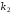 -число степеней свободы меньшей дисперсии) -число степеней свободы меньшей дисперсии)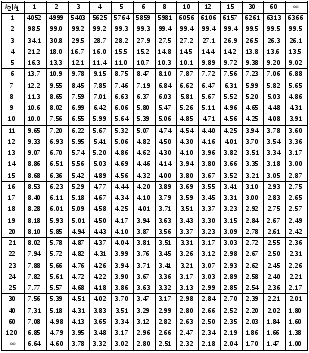 ПРИЛОЖЕНИЕ 5.2 Критические точки распределения Фишера 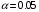 ( 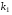 - число степеней свободы большей дисперсии, - число степеней свободы большей дисперсии, 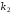 - число степеней свободы меньшей дисперсии) - число степеней свободы меньшей дисперсии) ПРИЛОЖЕНИЕ 6. ОСНОВНЫЕ ФОРМУЛЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 6.1. Основные числовые характеристики выборки.
6.2 Доверительные интервалы. Необходимый объём выборки. Доверительные интервалы для параметров  и и 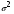 нормально распределённой генеральной совокупности. нормально распределённой генеральной совокупности.
Доверительный интервал для параметра 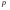 биномиального распределения. биномиального распределения.
| |||||||||||||||||||||||||||||||||

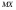 генеральной совокупности)
генеральной совокупности)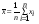
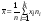
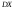 генеральной совокупности):
генеральной совокупности):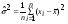
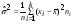
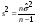
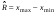
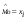 , где
, где 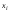 -элемент выборки, встречающийся с наибольшей частотой
-элемент выборки, встречающийся с наибольшей частотой 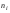 ; б)
; б)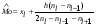 , где
, где 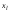 -нижняя граница модального интервала (интервала с наибольшей частотой);
-нижняя граница модального интервала (интервала с наибольшей частотой); 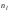 - частота модального интервала;
- частота модального интервала; 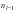 ,
, 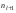 - частоты соседних интервалов;
- частоты соседних интервалов; 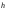 - длина интервала группировки.
- длина интервала группировки.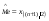 , если
, если  - нечётное число и
- нечётное число и 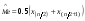 , если
, если 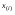 -элемент вариационного ряда выборки с номером
-элемент вариационного ряда выборки с номером 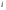 .
. 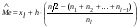 , где
, где 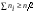 ;
; 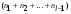 - число элементов выборки в интервалах, лежащих слева от медианного;
- число элементов выборки в интервалах, лежащих слева от медианного; 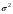 неизвестна)
неизвестна)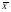
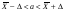 , где
, где 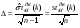 ,
, 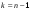
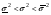 , где
, где 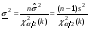 ,
, 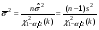 ,
,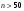 ,
,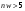 ,
,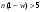 )
)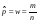
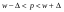 , где
, где