матанализ. Решение (x) 1 (x 2 1) 2x Здесь (x 2 ) 2x 21 (x) 2x (x) 1 Ответ

• Название: Решение (x) 1 (x 2 1) 2x Здесь (x 2 ) 2x 21 (x) 2x (x) 1 Ответ
• Дата: 15.11.2018
• Размер: 282 Kb.
• Имя файла: матанализ.doc
• Тип: Решение; #56610

Вариант 12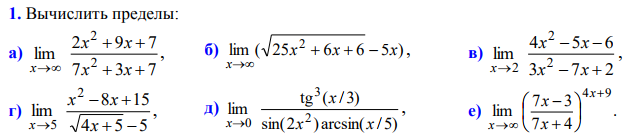



а) = =

б)







в) =

г)

Для выражения

сопряженным является

Умножим его на числитель и знаменатель.

=

Ответ:

Учитывая, что (a-b)(a+b) = a²-b², получаем:

д)

Используем свойство первого замечательного предела:

sin(2·x²) ≈ 2·x²

=

Ответ:

е) Используя свойства второго замечательного предела:

Получаем:

= = =

здесь a = -7, b = 4/7

Ответ:



а)

Решение:

= =

(x)ʹ = 1

(x²+1)ʹ = 2·x

Здесь:

(x²)ʹ = 2·x^2-1(x)ʹ = 2·x

(x)ʹ = 1

Ответ:

При вычислении были использованы следующие правила дифференцирования:

(x^a)' = ax^a-1

(a)' = 0

б) y=(x-sin(3·x))·cos(4·x)

Решение:

((x-sin(3·x))·cos(4·x))ʹ = (x-sin(3·x))ʹ·cos(4·x)+(x-sin(3·x))·(cos(4·x))ʹ = (-3·cos(3·x)+1)·cos(4·x)+(x-sin(3·x))·(-4·sin(4·x))

Здесь:

(x-sin(3·x))ʹ = (x)ʹ + (-sin(3·x))ʹ = 1 + (-3·cos(3·x)) = -3·cos(3·x)+1

(-sin(3·x))ʹ = (-sin(3·x))ʹ(3·x)ʹ = -3·cos(3·x)

(3·x)ʹ = 3

(cos(4·x))ʹ = (cos(4·x))ʹ(4·x)ʹ = -4·sin(4·x)

(4·x)ʹ = 4

Ответ:

-4·(x-sin(3·x))·sin(4·x)+(-3·cos(3·x)+1)·cos(4·x)

При вычислении были использованы следующие правила дифференцирования:

(x^a)' = ax^a-1

(a)' = 0

(uv)' = u'v + uv'

(f(g(x)))' = f(x)'*g(x)'

в)

Решение:

=

Решение ищем по формуле:

(a^f(x))' = a^f(x)*ln(a)*f(x)'

= =

Поскольку:

= =

=

Здесь:

(x²)ʹ = 2·x^2-1(x)ʹ = 2·x

(x)ʹ = 1

Ответ:

При вычислении были использованы следующие правила дифференцирования:

(x^a)' = ax^a-1

(a)' = 0

(f(g(x)))' = f(x)'*g(x)'

г) y=(tg(x))^arctg(x)

Решение:

=

Прологарифмируем обе части:

Тогда:

Находя производную, получаем:

=

Ответ:

При вычислении были использованы следующие правила дифференцирования:

(x^a)' = ax^a-1

(a)' = 0

(uv)' = u'v + uv'

(f(g(x)))' = f(x)'*g(x)'

(u^v)' = u^v(v*ln(u))'

д) x·sin(5·y)+y·cos(5·x)-x²+y²=0

Решение.

Поскольку функция задана в неявном виде, то производную ищем по формуле:

Для нашей функции:

Тогда:

или

е) x=t³+8·t

y=t⁵+2·t

Решение.

Функция задана в параметрическом виде. Параметрическое задание функции удобно тем, что оно дает общую запись для прямой и обратной функций.

Отдельно находим производные x_t' и y_t'

x_tʹ = 3·t²+8

y_tʹ = 5·t⁴+2

Следовательно:



Необходимое условие экстремума функции одной переменной.

Уравнение f'₀(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает.

Достаточное условие экстремума функции одной переменной.

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:

f'₀(x*) = 0

f''₀(x*) > 0

то точка x* является точкой локального (глобального) минимума функции.

Если в точке x* выполняется условие:

f'₀(x*) = 0

f''₀(x*) < 0

то точка x* - локальный (глобальный) максимум.

Решение.

Находим первую производную функции:

yʹ = 4·x³-4·x

или

yʹ = 4·x·(x²-1)

Приравниваем ее к нулю:

4·x³-4·x = 0

x₁ = -1

x₂ = 0

x₃ = 1

Вычисляем значения функции на концах отрезка

f(-1) = 4

f(0) = 5

f(1) = 4

f(-1) = 4

f(2) = 13

Ответ:

f_min = 4, f_max = 13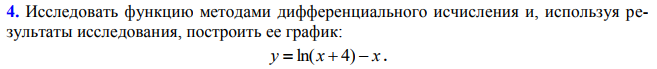



1) Область определения функции. Точки разрыва функции.

2) Четность или нечетность функции.

y(-x)=x+ln(-x+4)

Функция общего вида

3) Периодичность функции.

4) Точки пересечения кривой с осями координат.

Пересечение с осью 0Y

x=0, y=ln(4)

Пересечение с осью 0X

y=0

ln(x+4)-x=0

x = 1.749

5) Исследование на экстремум.

y = log(x+4)-x

При определении границ интервалов учитывайте область существования функции.

Область существования функции

1. Находим интервалы возрастания и убывания. Первая производная.

или

Находим нули функции. Для этого приравниваем производную к нулю

-x-3 = 0

Откуда:

x₁ = -3

f '(x) > 0	f '(x) < 0
функция возрастает	функция убывает

В окрестности точки x = -3 производная функции меняет знак с (+) на (-). Следовательно, точка x = -3 - точка максимума.

2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.

или

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

Для данного уравнения корней нет.

6) Асимптоты кривой.

y = ln(x+4)-x

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

Находим коэффициент k:

Находим коэффициент b:

Предел равен ∞, следовательно, наклонные асимптоты функции отсутствуют.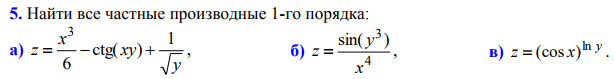



а) При нахождении ∂z/∂x считаем аргумент y постоянным:

При нахождении ∂z/∂y считаем аргумент x постоянным:

Найдем смешанные частные производные:

Для того, чтобы найти ∂²z/∂x∂y дифференцируем ∂z/∂x по у:

= =

б) Находим частные производные:

При нахождении ∂z/∂x считаем аргумент y постоянным:

При нахождении ∂z/∂y считаем аргумент x постоянным:

Найдем смешанные частные производные:

Для того, чтобы найти ∂²z/∂x∂y дифференцируем ∂z/∂x по у:

=

в) Находим частные производные по формулам:

Для нашей функции F(x,y,z):

При нахождении ∂F/∂x считаем y и z постоянными:

При нахождении ∂F/∂y считаем x и z постоянными:

При нахождении ∂F/∂z считаем x и y постоянными:

По формулам находим частные производные:

или

или



а)

=

б)

Делаем замену переменных:

t=6-7·x⁴

Тогда:

=

Возвращаемся к x:

Ответ:

в)

Поскольку R(sin(x),-cos(x)) = - R(sin(x),cos(x)), то делаем тригонометрическую подстановку: sin(x) = t и тогда cos(x)dx = dt

Упростим выражение:

Интегрируя, получаем:

Возвращаясь к замене переменных, получаем:

г) Формула интегрирования по частям:

Положим

U=ln(-5·x+3)

dV= dx

Тогда:

V = x

Поэтому:

Находим интеграл

Ответ:

д)

Подынтегральная функция может быть представлена в виде:

Используем метод разложения на простейшие. Разложим функцию на простейшие слагаемые:

Приравняем числители и учтем, что коэффициенты при одинаковых степенях x, стоящие слева и справа должны совпадать:

27*(x²-3) = A(x+3)² + B(x-6)(x+3) + C(x-6)

x²: A + B = 27

x: 6A -3B + C = 0

1: 9A -18B -6C = -3

Решая ее, находим:

A = ³²³/₂₇;B = ⁴⁰⁶/₂₇;C = ^-80/₃;

=

Вычисляем табличный интеграл:

Вычисляем табличный интеграл:

Вычисляем табличный интеграл:

Ответ:

е) Формула интегрирования по частям:

Положим

U=sin(x)⁴

dV= dx

Тогда:

dU = 4·sin(x)³·cos(x) dx

V = x

Поэтому:

Находим интеграл

В итоге получаем:

Поскольку это циклический интеграл, переносим полученное выражение интеграла в левую часть:

или

Разделим правую часть на общий множитель.

Ответ:



а)

Наименьшее общее кратное чисел 1,3,3 равно 3. Поэтому делаем замену x = t³. Тогда dx = 3*t^2*dt и:

Упростим дробное выражение:

Степень числителя P(x) больше или равна степени знаменателя Q(x), поэтому разделим полиномы.

Интегрируя целую часть, получаем:

Интегрируя далее, получаем:

Ответ:

-6·t⁵+15·t⁴ + C

Подставляя вместо t=(x)^1/3, получаем:

Вычислим определенный интеграл:

F(27) = -243

F(1) = 9

I = -243 - (9) = -252

б)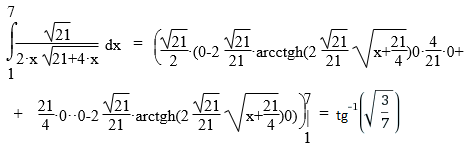



в) Формула интегрирования по частям:

Положим

U=x

Тогда:

dU = dx

Поэтому:

Находим интеграл

Ответ:

Вычислим определенный интеграл:

F(0) = 6