Решение 2012 Овд 2011г 2012г задача 15
 Скачать 228.19 Kb. Скачать 228.19 Kb.
|
|
А) средний процент изменения выпуска продукции по сравнению с базисным периодом: 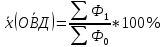 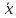 = Выпуск в отч. периоде / Выпуск в базисном периоде = Выпуск в отч. периоде / Выпуск в базисном периоде 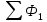 = 7570 = 7570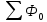 = 2440/0,955 + 2520/1,036 + 2610/1,052 = 7468,39 = 2440/0,955 + 2520/1,036 + 2610/1,052 = 7468,39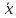 = 7570/7468,39 = 1,014 или 101,4% => Средний процент прироста равен + 1,4% = 7570/7468,39 = 1,014 или 101,4% => Средний процент прироста равен + 1,4%Б) средний удельный вес экспортируемой продукции в фактическом выпуске отчетного периода:  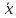 = экспортируемая продукция / Выпуск в отч. периоде = (2440*0,25 + 2520*0,12 + 2610*0,15) / (2440 + 2520 + 2610) = 1303,9 / 7570 = 0,1722 - средняя арифметич. взвеш. Или 17,22% = экспортируемая продукция / Выпуск в отч. периоде = (2440*0,25 + 2520*0,12 + 2610*0,15) / (2440 + 2520 + 2610) = 1303,9 / 7570 = 0,1722 - средняя арифметич. взвеш. Или 17,22%ЗАДАЧА 7.22
Определите моду и медиану роста студентов, квартили, децили и тд.
1) 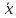 = ∑Xi* fi / ∑fi = 45360/265 = 171.2 = ∑Xi* fi / ∑fi = 45360/265 = 171.22) МОДА: 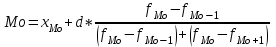 где где хМо – нижняя граница модального интервала; d – величина модального интервала; fМо – частота модального интервала; fМо-1 – частота, предшествующая модальному интервалу; fМо+1 – частота интервала, следующего за модальным. fmax = 60 => модальный интервал 170-174 d = 4 т.к. 164-160=168-164=4 Мо = 170 + 4 *[ (60-45) / ( (60-45) + (60-40) ) ] = 171,71 см 3)МЕДИАНА: 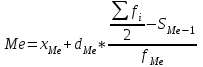 где где хМе – нижняя граница медианного интервала; dМе – величина медианного интервала; fМе – частота медианного интервала; SМе-1 – сумма накопленных частот, предшествующих медианному интервалу; åfi/2 = 265/2 = 132,5 => медианный интервал 170-174 т.к. первая Sn превыш 132,5 это 175 dМе = 4 т.к. 164-160=168-164=4 Me = 170 + 4 *[(132,5 - 45) / 60] = 175,84 см 4)КВАРТИЛИ 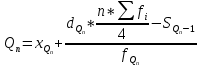 Первый: 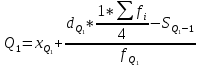 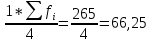 => интервал 162-166 т.к. Sn=70 (первая превышает 66,25) => интервал 162-166 т.к. Sn=70 (первая превышает 66,25)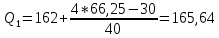 Третий: 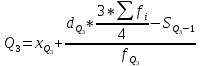 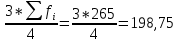 => интервал 174-178 т.к. Sn=215 (первая превышает 198,75) => интервал 174-178 т.к. Sn=215 (первая превышает 198,75)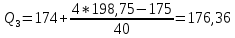 5) ДЕЦИЛИ 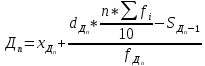 Второй: 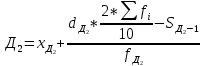 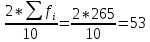 => интервал 162-166 т.к. Sn=70 (первая превышает 53) => интервал 162-166 т.к. Sn=70 (первая превышает 53)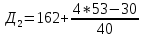 =164,3 =164,3Восьмой: 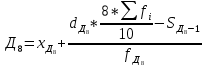 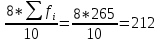 => интервал 174-178 т.к. Sn=215 (первая превышает 212) => интервал 174-178 т.к. Sn=215 (первая превышает 212)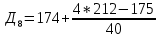 =177,7 =177,7Первый, седьмой и девятый децили рассчитываются по тому же принципу, меняя только в формуле число «8/10» на «1/10» , «7/10», «9/10». 6)ПОКАЗАТЕЛИ ВАРИАЦИИ: 1. 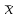 = ∑ Xi* fi / ∑ fi = 171,2 = ∑ Xi* fi / ∑ fi = 171,22. Размах вариации R = xmax – xmin = 186-158 = 28 3. Среднее линейное отклонение - для несгруппированных данных (первичного ряда): 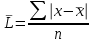 -для вариационного ряда: 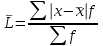 = 1528/265 = 5,77 = 1528/265 = 5,774. Дисперсия - для несгруппированных данных: 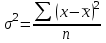 - для вариационного ряда: 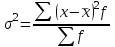 = 12857,6/265 = 48,52 = 12857,6/265 = 48,52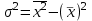 5. Среднее квадратическое отклонение 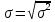 = 6,97 = 6,976. Коэффициент вариации 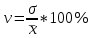 - до 17% – совокупность совершенно однородна, 17%-33% - достаточно однородна, >33% - неоднородна. - до 17% – совокупность совершенно однородна, 17%-33% - достаточно однородна, >33% - неоднородна.V = (6,97 / 171,2) * 100% = 4,07% 7. Коэффициент вариации линейный (относительное линейное отклонение) V = ( 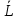 / /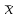 ) * 100% = ( 5,77 / 171,2) * 100% = 3,37% ) * 100% = ( 5,77 / 171,2) * 100% = 3,37%
V = (R / 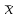 ) * 100% = (28/171,2) *100 = 16,35% ) * 100% = (28/171,2) *100 = 16,35%ЗАДАЧА 7.24 Имеются данные по филиалам организации за год
Определите: А) средний уровень фондоотдачи Б) среднюю стоимость основных фондов в расчете на 1 филиал В) средний уровень фондовооруженности труда Г) средний удельный вес продукции, реализуемой за пределами региона Решение: А) Расчет по средней арифметической взвешанной. f-графа2 х-графа1 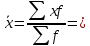 (1*2+3*3+5*4+7*2)/(2+3+4+2)=4.09 руб. (1*2+3*3+5*4+7*2)/(2+3+4+2)=4.09 руб.Б) Расчет по средней арифметической взвешанной. f-графа2 х-графа3 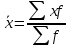 = (80*2+96*3+100*4+110*2)/(2+3+4+2) = 97 млн.руб. = (80*2+96*3+100*4+110*2)/(2+3+4+2) = 97 млн.руб.В) Расчет по средней арифметической взвешанной. f-графа2 х-графа4 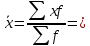 (2*1300+3*1420+4*1500+2*1680)/(2+3+4+2)=1474.5 (2*1300+3*1420+4*1500+2*1680)/(2+3+4+2)=1474.5Г) Расчет по средней арифметической взвешанной. f-графа2 х-графа5 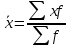 = (2*2.4+3*2.8+4*2.7+2*2.9)/(2+3+4+2)=2.71 = (2*2.4+3*2.8+4*2.7+2*2.9)/(2+3+4+2)=2.71ЗАДАЧА 7.27 Распределение населения по величине среднедушевых денежных доходов в 2010 г.характеризуют следующие данные.
Определите: А) среднедушевые денежные доходы Б) медиану, квартили, децили для данного ряда распределения В) долю населения, имевшего доходы ниже прожиточного минимума, если последний составляет в среднем 5688 руб. на душу населения Г) уровень, который не превышает среднедушевые денежные доходы 20% граждан, имеющих наименьшие доходы. Решение: А) Расчет по средней арифметической взвешанной. х- 1 графа, f=2графа 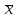 = =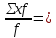 (2.75*3.9+4.25*5.6+6*9.4+8.5*14.7+12.5*20.2+20*23.5+30*10.8+40*11.9)/100=17.38 (2.75*3.9+4.25*5.6+6*9.4+8.5*14.7+12.5*20.2+20*23.5+30*10.8+40*11.9)/100=17.38Б) см7.22 В) доля "до 3,5", 3,5-5 и часть доли из интервала 3,5-5-7 =0,039+0,056+(5688-5000)/(7000-5000)*0,094=0,13 Г) По сумме накопленных частот вычисляем, 20%-18,9%, тк 33,60% первая превышает 20%(в условии) => 7-10 интервал (20%-18,9%)/(33,6%-18,9%)=7,48% Значение будет в =7+7,48%*(10-7)=7,2 ЗАДАЧА 8.14
Рассчитать: А) размах вариации Б) среднее линейное отклонение В) дисперсию Г) среднее квадратическое отклонение Д) коэффициент вариации Решение: А) R = xmax - xmin = 55-18 = 37 Б) т.к. данные не сгруппированы: средняя арифметическая простая 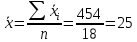 тыс.руб. тыс.руб. 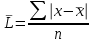 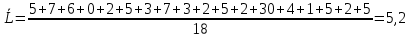 тыс.руб. тыс.руб.В) 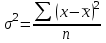 т.к. не сгруппированные данные т.к. не сгруппированные данные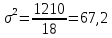 Г) 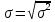 = 8,2 = 8,2Д) 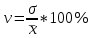 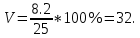 ЗАДАЧА 8.17
Вычислить абсолютные и относительные показатели вариации Решение: 1. 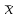 = ∑ Xi* fi / ∑ fi = (126+299+550+972+290+217+198)/100=27 мин. = ∑ Xi* fi / ∑ fi = (126+299+550+972+290+217+198)/100=27 мин.2. Размах вариации R = xmax – xmin = 33-21 = 12 3. Среднее линейное отклонение 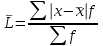 = 21.6 = 21.64. Дисперсия 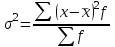 = 9.6 = 9.65. Среднее квадратическое отклонение 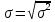 = 3.1 = 3.16. Коэффициент вариации 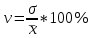 V = (3.1 /27) * 100% = 11.5% V = (3.1 /27) * 100% = 11.5%7. Коэффициент вариации линейный (относительное линейное отклонение) V = ( 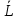 / /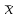 ) * 100% = ( 21.6 / 27) * 100% = 80% ) * 100% = ( 21.6 / 27) * 100% = 80%8. Коэффициент ассоциации V = (R / 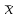 ) * 100% = (12/27) *100 = 44.4% ) * 100% = (12/27) *100 = 44.4% |
