Лекция. Уравнение прямой на плоскости
1.Расстояние между точками
Даны две точки 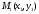 и и 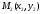 . Требуется найти расстояние между ними (рис. 1). . Требуется найти расстояние между ними (рис. 1).
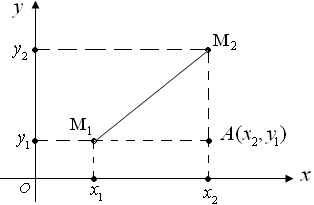
Рис. 1
По теореме Пифагора длина гипотенузы равна квадратному корню из суммы квадратов длин катетов:
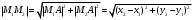 . (1) . (1)
Пример 1. Найти расстояние между точками 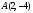 и и 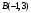 . .
Решение. 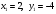 ; ; 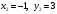 . По формуле (1) . По формуле (1) 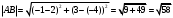 . .
2. Прямая линия на плоскости
1) каноническое уравнение прямой на плоскости
Известна точка 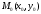 , через которую проходит прямая и направляющий вектор прямой , через которую проходит прямая и направляющий вектор прямой
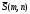 , коллинеарный данной прямой (рис. 2). Пусть , коллинеарный данной прямой (рис. 2). Пусть 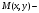 произвольная точка на прямой (текущая точка). произвольная точка на прямой (текущая точка).
Векторы 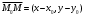 и и 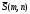 коллинеарны, поэтому координаты этих векторов пропорциональны: коллинеарны, поэтому координаты этих векторов пропорциональны:
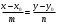 . (2) . (2)
Уравнение (2) называется каноническим уравнением прямой.
Пример 2. Составить уравнение прямой, проходящей через точку 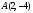 параллельно вектору параллельно вектору 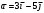 . Решение. По условию . Решение. По условию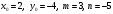 . По формуле (2) уравнение прямой примет вид . По формуле (2) уравнение прямой примет вид 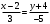 . .
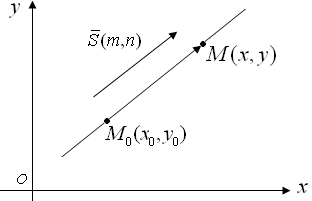
Рис. 2
2) Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Рассмотрим прямую, проходящую через точку 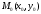 , перпендикулярно вектору , перпендикулярно вектору 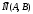 (рис. 3). Причем (рис. 3). Причем 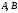 одновременно не обращаются в нуль. Возьмем на прямой текущую точку одновременно не обращаются в нуль. Возьмем на прямой текущую точку 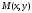 и построим вектор и построим вектор 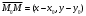 . Векторы . Векторы 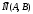 и и 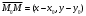 перпендикулярны, отсюда их скалярное произведение равно нулю: перпендикулярны, отсюда их скалярное произведение равно нулю:
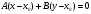 . (3) . (3)
Уравнение (3) называется уравнением прямой, проходящей через данную точку перпендикулярно данному вектору.
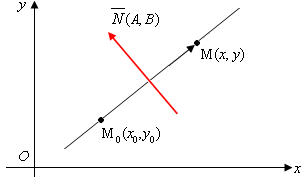
Рис. 3
Вектор 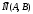 называется нормальным вектором прямой. За нормальный вектор прямой можно принять любой вектор, перпендикулярный данной прямой. называется нормальным вектором прямой. За нормальный вектор прямой можно принять любой вектор, перпендикулярный данной прямой.
Уравнения (2) и (3) есть уравнения первой степени относительно текущих координат  и и 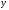 . .
Утверждение. Всякое уравнение первой степени относительно текущих координат  и и 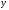 определяет на плоскости прямую. Рассмотрим уравнение первой степени относительно текущих координат определяет на плоскости прямую. Рассмотрим уравнение первой степени относительно текущих координат
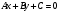 , (4) , (4)
причем 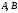 одновременно не обращаются в нуль. Всегда можно подобрать пару чисел одновременно не обращаются в нуль. Всегда можно подобрать пару чисел 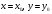 , которые удовлетворяют этому уравнению: , которые удовлетворяют этому уравнению: 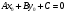 . Полученное тождество вычтем почленно из уравнения (4): . Полученное тождество вычтем почленно из уравнения (4): 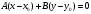 . Мы доказали, что (4) есть уравнение прямой, проходящей через данную точку . Мы доказали, что (4) есть уравнение прямой, проходящей через данную точку 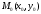 перпендикулярно данному вектору перпендикулярно данному вектору 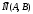 . .
Всякое уравнение первой степени относительно текущих координат называется линейным.
3) Уравнение прямой общего вида и его исследование
Линейное уравнение
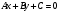 , (5) , (5)
называется уравнением прямой общего вида. В этом уравнении 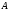 и и 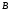 координаты нормального вектора прямой координаты нормального вектора прямой 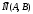 , а , а 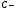 свободный член, причем свободный член, причем 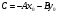 . .
Исследуем общее уравнение прямой (5). Для этого выясним, как будет расположена прямая, если коэффициенты 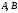 и и 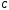 поочередно и попарно обратятся в ноль. поочередно и попарно обратятся в ноль.
1. 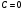 . Тогда уравнение (5) примет вид: . Тогда уравнение (5) примет вид: 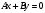 . Это уравнение прямой, проходящей через начало координат. Действительно, координаты точки . Это уравнение прямой, проходящей через начало координат. Действительно, координаты точки 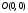 удовлетворяют данному уравнению (рис. 4). удовлетворяют данному уравнению (рис. 4).
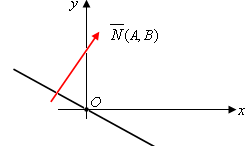
Рис. 4
2. 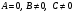 . Тогда уравнение (5) примет вид: . Тогда уравнение (5) примет вид: 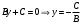 . В этом случае нормальный вектор . В этом случае нормальный вектор 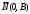 . Мы видим, что проекция нормального вектора прямой на ось . Мы видим, что проекция нормального вектора прямой на ось 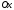 равна нулю, а это означает, что этот вектор перпендикулярен оси равна нулю, а это означает, что этот вектор перпендикулярен оси 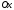 . Отсюда следует, что сама прямая параллельна оси . Отсюда следует, что сама прямая параллельна оси  (рис. 5). (рис. 5).
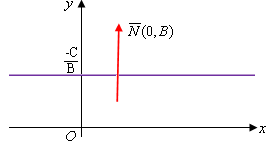
Рис. 5
3. 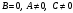 . Тогда уравнение (5) примет вид: . Тогда уравнение (5) примет вид: 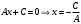 . В этом случае нормальный вектор . В этом случае нормальный вектор 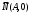 . Мы видим, что проекция нормального вектора прямой на ось . Мы видим, что проекция нормального вектора прямой на ось 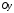 равна нулю, а это означает, что этот вектор перпендикулярен оси равна нулю, а это означает, что этот вектор перпендикулярен оси 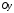 . Отсюда следует, что сама прямая параллельна оси . Отсюда следует, что сама прямая параллельна оси 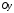 (рис. 6). (рис. 6).
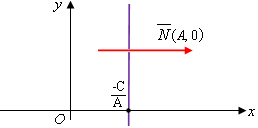
Рис. 6
4. 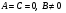 . Тогда уравнение (5) примет вид: . Тогда уравнение (5) примет вид: 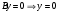 . Это уравнение оси . Это уравнение оси 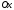 . .
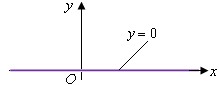
Рис. 7
5. 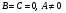 . Тогда уравнение (5) примет вид: . Тогда уравнение (5) примет вид: 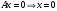 . Это уравнение оси . Это уравнение оси 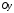 . .
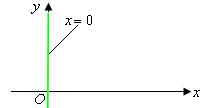
Рис. 8
4) Уравнение прямой, проходящей через данную точку в данном направлении
Дано каноническое уравнение прямой 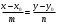 . Перепишем его в виде . Перепишем его в виде 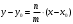 . Параллельным переносом переместим направляющий вектор прямой . Параллельным переносом переместим направляющий вектор прямой 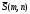 так, чтобы его начало совпало с началом координат (рис. 9). так, чтобы его начало совпало с началом координат (рис. 9).
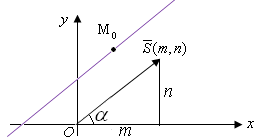
Рис. 9
Из рис. 9 следует, что 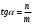 , или , или 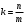 . Тогда уравнение прямой, проходящей через данную точку в данном направлении примет вид: . Тогда уравнение прямой, проходящей через данную точку в данном направлении примет вид:
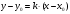 (6) Важное уравнение (6) Важное уравнение
Пример. Составить уравнение прямой, проходящей через точку А(-3,7) и образующей с осью 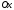 угол угол 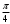 . .
Решение. По условию 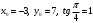 , тогда , тогда 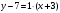 , или , или 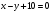 . .
Пример 3. Проверить, принадлежат ли точки 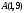 и и 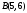 прямой прямой 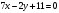 . .
Решение. Если координаты точки удовлетворяют уравнению, т.е. обращают его в тождество, то эта точка принадлежит данной прямой; если же координаты точки не удовлетворяют уравнению, то точка не принадлежит прямой.
Подставив вместо переменных  и и 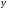 в уравнение в уравнение 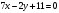 координаты точки координаты точки 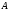 , получим тождество , получим тождество 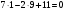 , следовательно, точка , следовательно, точка 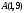 принадлежит данной прямой. Аналогично убеждаемся, что точка принадлежит данной прямой. Аналогично убеждаемся, что точка 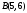 – не принадлежит. – не принадлежит.
5) Уравнение прямой с угловым коэффициентом
Пусть прямая пересекает ось 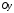 в точке в точке 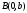 и образует с положительным направлением оси и образует с положительным направлением оси 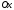 угол угол  (рис. 10). (рис. 10).
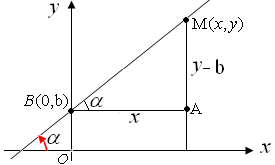
Рис. 10
Из треугольника ВМА находим, что катет 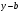 можно выразить через катет можно выразить через катет : : 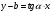 , где , где 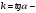 угловой коэффициент прямой ВМ. Т.о., уравнение прямой с угловым коэффициентом примет вид: угловой коэффициент прямой ВМ. Т.о., уравнение прямой с угловым коэффициентом примет вид:
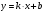 , (7) , (7)
где 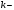 тангенс угла между прямой ВМ и положительным направлением оси тангенс угла между прямой ВМ и положительным направлением оси 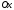 . Отсчет угла ведется от положительного направления оси . Отсчет угла ведется от положительного направления оси 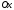 против хода часовой стрелки. против хода часовой стрелки.
Пример. Составить уравнение прямой, проходящей через точку А(3,4) и отсекающей на оси 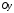 отрезок отрезок 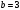 . .
Решение. Подставим в уравнение (5)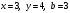 : : 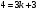 . Отсюда . Отсюда 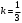 . Тогда искомое уравнение имеет вид: . Тогда искомое уравнение имеет вид: 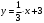 . .
6) Уравнение прямой, проходящей через две данные точки
Даны две точки 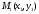 и и 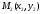 . Требуется составить уравнение прямой, проходящей через эти точки (рис. 11). . Требуется составить уравнение прямой, проходящей через эти точки (рис. 11).
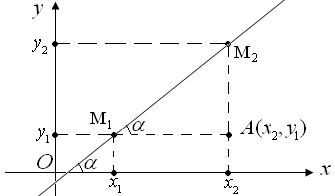
Рис. 11
Сначала найдем угловой коэффициент прямой, проходящей через две данные точки. Из треугольника 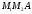 находим находим
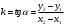 . (8) . (8)
В формулу (6) вместо 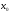 подставим подставим 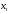 , а вместо , а вместо 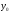 подставим подставим 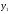 . Вместо . Вместо 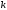 – дробь – дробь
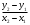 . Тогда получим . Тогда получим 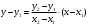 , или , или
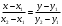 . (9) . (9)
Пример. Составить уравнение прямой, проходящей через две данные точки А(-2,6) и В(4, 9).
Решение. По условию 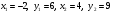 . Тогда по формуле (9) находим . Тогда по формуле (9) находим 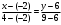 , или , или 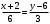 . .
7) Уравнение прямой в отрезках
Пусть прямая отсекает по оси 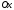 отрезок отрезок  и по оси и по оси 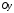 отрезок отрезок 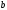 (рис. 12). Возьмем на прямой текущую точку (рис. 12). Возьмем на прямой текущую точку 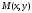 . Треугольник . Треугольник 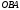 подобен треугольнику подобен треугольнику 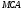 . .
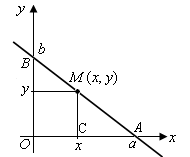
Рис. 12
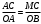 или или 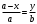 . После почленного деления в левой части находим . После почленного деления в левой части находим 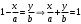 . .
Т.о., уравнение прямой в отрезках имеет вид
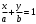 . (10) . (10)
Пример. Найти отрезки, которые прямая 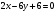 отсекает по осям координат. отсекает по осям координат.
Решение. Запишем уравнение в виде 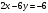 . Поделим обе части уравнения на (-6): . Поделим обе части уравнения на (-6):
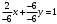 или или 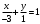 . Отсюда прямая отсекает по оси . Отсюда прямая отсекает по оси 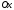 отрезок отрезок 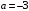 и по оси и по оси 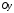 отрезок отрезок 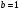 . .
3. Уравнение пучка прямых
Даны две прямые 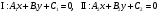 , которые пересекаются в точке , которые пересекаются в точке 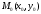 (рис. 13а). (рис. 13а).
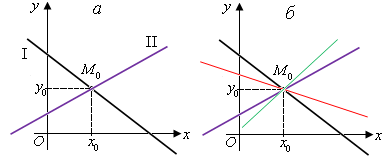
Рис. 13
Семейство прямых, проходящих через точку пересечения данных двух прямых называется пучком прямых (рис. 13б).
Уравнения пучка прямых имеет вид
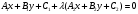 . (11) . (11)
Здесь 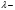 произвольный параметр. произвольный параметр.
Пример. Из пучка прямых, проходящих через точку пересечения прямых 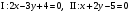 , выделить прямую, проходящую параллельно оси , выделить прямую, проходящую параллельно оси 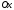 . .
Решение. Запишем уравнение пучка по формуле (11): 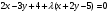 . Раскроем скобки и найдем нормальный вектор последней прямой: . Раскроем скобки и найдем нормальный вектор последней прямой:
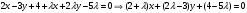 . (*) . (*)
Нормальный вектор прямой имеет координаты 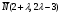 . Поскольку искомая прямая проходит параллельно оси . Поскольку искомая прямая проходит параллельно оси 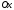 , то нормальный вектор будет перпендикулярен оси , то нормальный вектор будет перпендикулярен оси 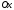 и и 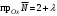 должна быть равна нулю: должна быть равна нулю: 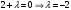 . Подставим . Подставим 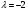 в формулу (*): в формулу (*):
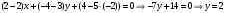 . .
4. Расстояние от точки до прямой
Расстояние от точки 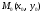 до прямой до прямой 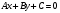 находится по формуле: находится по формуле:
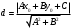 . (12) . (12)
5. Угол между двумя прямыми
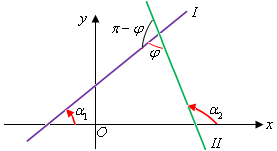
Рис. 14
Две пересекающиеся прямые, если они не перпендикулярны, образуют два различных по величине угла – острый угол 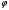 (рис. 14) и тупой (рис. 14) и тупой 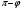 . .
Углом между двумя прямыми I и II называют угол 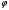 , на который надо повернуть первую прямую, чтобы она совпала с прямой II. Пусть первая прямая образует с осью , на который надо повернуть первую прямую, чтобы она совпала с прямой II. Пусть первая прямая образует с осью 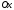 угол угол 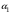 , а вторая угол , а вторая угол 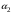 . .
Внешний угол треугольника равен сумме двух внутренних не смежных с ним: 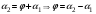 . .
Отсюда 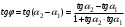 . Поскольку . Поскольку 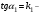 угловой коэффициент первой прямой, а угловой коэффициент первой прямой, а 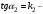 угловой коэффициент второй прямой, то угловой коэффициент второй прямой, то
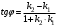 . Если прямые паралельны то их угловые коифиценты равны (13) . Если прямые паралельны то их угловые коифиценты равны (13)
Пример. Найти острый угол между прямыми 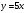 и и 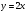 . .
Решение. По условию 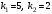 . Поскольку тангенс острого угла величина положительная, то в формуле (13) правую часть берем по модулю: . Поскольку тангенс острого угла величина положительная, то в формуле (13) правую часть берем по модулю: 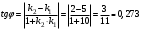 . .
Тогда 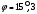 . .
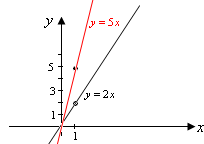
Рис. 15
6. Условие параллельности и перпендикулярности двух прямых
Даны две параллельные прямые 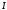 и и 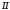 (рис. 16 a). Из рисунка видно, что если прямые параллельны, то их угловые коэффициенты равны, т.е. (рис. 16 a). Из рисунка видно, что если прямые параллельны, то их угловые коэффициенты равны, т.е.
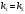 . (13) . (13)
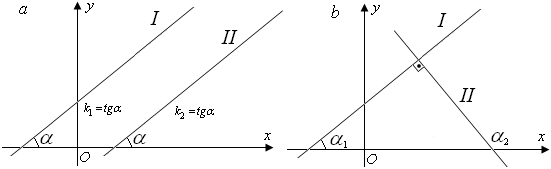
Рис. 16
Если прямые 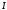 и и 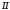 перпендикулярны (рис. 16 b), то их угловые коэффициенты обратны по величине и противоположны по знаку: перпендикулярны (рис. 16 b), то их угловые коэффициенты обратны по величине и противоположны по знаку:
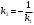 . (14) Доказательство. Угол . (14) Доказательство. Угол 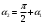 (рис. 16b). Тогда (рис. 16b). Тогда 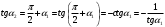 , или , или 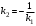 . .
Пример. Составить уравнение прямой, проходящей через точку А(4,-7) перпендикулярно прямой 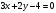 . .
Решение. Найдем угловой коэффициент прямой 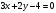 : : 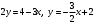 . Т.о., угловой коэффициент прямой . Т.о., угловой коэффициент прямой 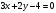 равен равен 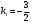 . Поскольку искомая прямая перпендикулярна прямой . Поскольку искомая прямая перпендикулярна прямой 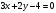 , то ее угловой коэффициент равен , то ее угловой коэффициент равен 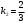 . .
По условию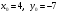 . Теперь по формуле (6) . Теперь по формуле (6) 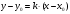 находим уравнение искомой прямой: находим уравнение искомой прямой: 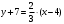 , или , или 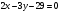 . .
Пример. Найти уравнение прямой, проходящей через точку пересечения прямых 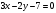 и и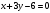 и отсекающей на оси абсцисс отрезок, равный 3. и отсекающей на оси абсцисс отрезок, равный 3.
Решение. Найдем точку пересечения прямых 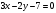 и и 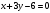 . Для этого решим систему . Для этого решим систему 
Из второго уравнения находим 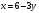 . Подставим в первое уравнение . Подставим в первое уравнение 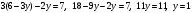 . Тогда . Тогда 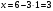 . Точка пересечения прямых имеет координаты . Точка пересечения прямых имеет координаты 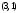 . По условию . По условию 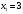 при при 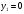 . Кроме того, . Кроме того, 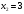 при при 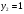 . .
По формуле (9) 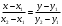 : : 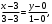 по свойству пропорции по свойству пропорции 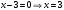 . .
Пример. Доказать, что четырехугольник 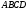 трапеция, если трапеция, если 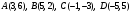 . .
Решение. Если в четырехугольнике параллельны две противоположные стороны, то это трапеция. Рассмотрим векторы 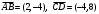 . Эти векторы коллинеарны, т.к. их координаты пропорциональны: . Эти векторы коллинеарны, т.к. их координаты пропорциональны: 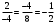 . Поэтому . Поэтому 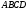 – трапеция. – трапеция.
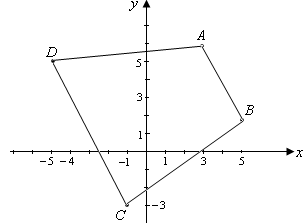
Рис. 17
Самостоятельно.
Пример 1. Написать уравнение прямой, проходящей через точку 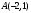 параллельно прямой параллельно прямой 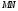 , ,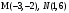 . .
Указание. Найти угловой коэффициент прямой 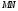 , затем применить формулу (6) – уравнение прямой, проходящей через данную точку в данном направлении. , затем применить формулу (6) – уравнение прямой, проходящей через данную точку в данном направлении.
Ответ: 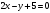 . .
Пример 2. Составить уравнение прямой, проходящей через точку А(3,1) перпендикулярно к прямой 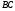 , ,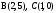 . .
Ответ: 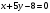 . .
|
 Скачать 404.75 Kb.
Скачать 404.75 Kb.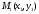 и
и 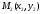 . Требуется найти расстояние между ними (рис. 1).
. Требуется найти расстояние между ними (рис. 1).

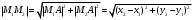 . (1)
. (1)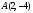 и
и 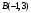 .
.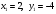 ;
; 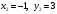 . По формуле (1)
. По формуле (1) 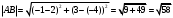 .
.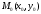 , через которую проходит прямая и направляющий вектор прямой
, через которую проходит прямая и направляющий вектор прямой 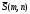 , коллинеарный данной прямой (рис. 2). Пусть
, коллинеарный данной прямой (рис. 2). Пусть 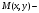 произвольная точка на прямой (текущая точка).
произвольная точка на прямой (текущая точка).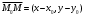 и
и 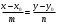 . (2)
. (2)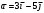 . Решение. По условию
. Решение. По условию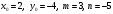 . По формуле (2) уравнение прямой примет вид
. По формуле (2) уравнение прямой примет вид 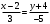 .
.
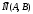 (рис. 3). Причем
(рис. 3). Причем 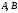 одновременно не обращаются в нуль. Возьмем на прямой текущую точку
одновременно не обращаются в нуль. Возьмем на прямой текущую точку 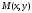 и построим вектор
и построим вектор 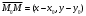 . Векторы
. Векторы 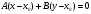 . (3)
. (3)
 и
и 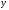 .
.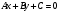 , (4)
, (4)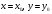 , которые удовлетворяют этому уравнению:
, которые удовлетворяют этому уравнению: 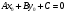 . Полученное тождество вычтем почленно из уравнения (4):
. Полученное тождество вычтем почленно из уравнения (4): 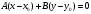 . Мы доказали, что (4) есть уравнение прямой, проходящей через данную точку
. Мы доказали, что (4) есть уравнение прямой, проходящей через данную точку 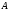 и
и 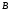 координаты нормального вектора прямой
координаты нормального вектора прямой 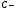 свободный член, причем
свободный член, причем 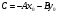 .
.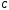 поочередно и попарно обратятся в ноль.
поочередно и попарно обратятся в ноль.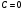 . Тогда уравнение (5) примет вид:
. Тогда уравнение (5) примет вид: 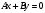 . Это уравнение прямой, проходящей через начало координат. Действительно, координаты точки
. Это уравнение прямой, проходящей через начало координат. Действительно, координаты точки 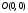 удовлетворяют данному уравнению (рис. 4).
удовлетворяют данному уравнению (рис. 4).
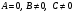 . Тогда уравнение (5) примет вид:
. Тогда уравнение (5) примет вид: 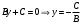 . В этом случае нормальный вектор
. В этом случае нормальный вектор 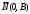 . Мы видим, что проекция нормального вектора прямой на ось
. Мы видим, что проекция нормального вектора прямой на ось 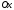 равна нулю, а это означает, что этот вектор перпендикулярен оси
равна нулю, а это означает, что этот вектор перпендикулярен оси 
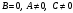 . Тогда уравнение (5) примет вид:
. Тогда уравнение (5) примет вид: 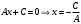 . В этом случае нормальный вектор
. В этом случае нормальный вектор 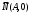 . Мы видим, что проекция нормального вектора прямой на ось
. Мы видим, что проекция нормального вектора прямой на ось 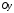 равна нулю, а это означает, что этот вектор перпендикулярен оси
равна нулю, а это означает, что этот вектор перпендикулярен оси 
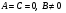 . Тогда уравнение (5) примет вид:
. Тогда уравнение (5) примет вид: 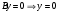 . Это уравнение оси
. Это уравнение оси 
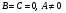 . Тогда уравнение (5) примет вид:
. Тогда уравнение (5) примет вид: 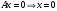 . Это уравнение оси
. Это уравнение оси 
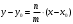 . Параллельным переносом переместим направляющий вектор прямой
. Параллельным переносом переместим направляющий вектор прямой 
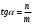 , или
, или 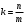 . Тогда уравнение прямой, проходящей через данную точку в данном направлении примет вид:
. Тогда уравнение прямой, проходящей через данную точку в данном направлении примет вид: 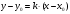 (6) Важное уравнение
(6) Важное уравнение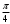 .
.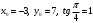 , тогда
, тогда 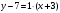 , или
, или 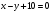 .
.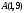 и
и 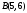 прямой
прямой 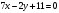 .
. и
и 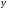 в уравнение
в уравнение 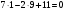 , следовательно, точка
, следовательно, точка 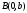 и образует с положительным направлением оси
и образует с положительным направлением оси  (рис. 10).
(рис. 10).
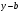 можно выразить через катет
можно выразить через катет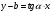 , где
, где 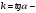 угловой коэффициент прямой ВМ. Т.о., уравнение прямой с угловым коэффициентом примет вид:
угловой коэффициент прямой ВМ. Т.о., уравнение прямой с угловым коэффициентом примет вид: 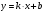 , (7)
, (7)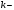 тангенс угла между прямой ВМ и положительным направлением оси
тангенс угла между прямой ВМ и положительным направлением оси 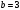 .
. 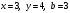 :
: 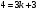 . Отсюда
. Отсюда 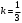 . Тогда искомое уравнение имеет вид:
. Тогда искомое уравнение имеет вид: 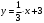 .
. 
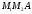 находим
находим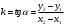 . (8)
. (8) 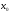 подставим
подставим 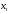 , а вместо
, а вместо 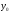 подставим
подставим 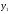 . Вместо
. Вместо 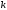 – дробь
– дробь 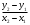 . Тогда получим
. Тогда получим 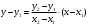 , или
, или 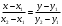 . (9)
. (9)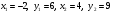 . Тогда по формуле (9) находим
. Тогда по формуле (9) находим 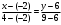 , или
, или 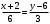 .
. и по оси
и по оси 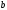 (рис. 12). Возьмем на прямой текущую точку
(рис. 12). Возьмем на прямой текущую точку 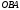 подобен треугольнику
подобен треугольнику 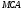 .
. 
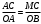 или
или 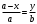 . После почленного деления в левой части находим
. После почленного деления в левой части находим 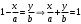 .
.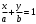 . (10)
. (10)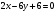 отсекает по осям координат.
отсекает по осям координат.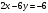 . Поделим обе части уравнения на (-6):
. Поделим обе части уравнения на (-6): 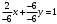 или
или 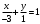 . Отсюда прямая отсекает по оси
. Отсюда прямая отсекает по оси 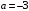 и по оси
и по оси 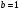 .
.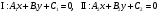 , которые пересекаются в точке
, которые пересекаются в точке 
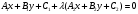 . (11)
. (11) 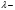 произвольный параметр.
произвольный параметр.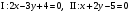 , выделить прямую, проходящую параллельно оси
, выделить прямую, проходящую параллельно оси 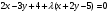 . Раскроем скобки и найдем нормальный вектор последней прямой:
. Раскроем скобки и найдем нормальный вектор последней прямой: 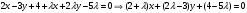 . (*)
. (*)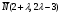 . Поскольку искомая прямая проходит параллельно оси
. Поскольку искомая прямая проходит параллельно оси 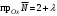 должна быть равна нулю:
должна быть равна нулю: 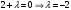 . Подставим
. Подставим 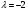 в формулу (*):
в формулу (*): 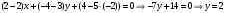 .
.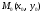 до прямой
до прямой 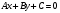 находится по формуле:
находится по формуле: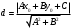 . (12)
. (12)
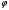 (рис. 14) и тупой
(рис. 14) и тупой 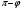 .
. 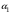 , а вторая угол
, а вторая угол 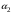 .
.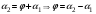 .
.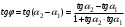 . Поскольку
. Поскольку 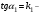 угловой коэффициент первой прямой, а
угловой коэффициент первой прямой, а 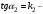 угловой коэффициент второй прямой, то
угловой коэффициент второй прямой, то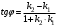 . Если прямые паралельны то их угловые коифиценты равны (13)
. Если прямые паралельны то их угловые коифиценты равны (13)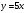 и
и 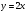 .
.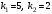 . Поскольку тангенс острого угла величина положительная, то в формуле (13) правую часть берем по модулю:
. Поскольку тангенс острого угла величина положительная, то в формуле (13) правую часть берем по модулю: 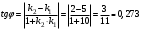 .
.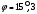 .
.
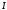 и
и 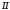 (рис. 16 a). Из рисунка видно, что
(рис. 16 a). Из рисунка видно, что 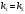 . (13)
. (13)
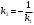 . (14) Доказательство. Угол
. (14) Доказательство. Угол 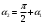 (рис. 16b). Тогда
(рис. 16b). Тогда 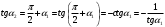 , или
, или 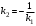 .
.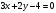 .
.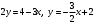 . Т.о., угловой коэффициент прямой
. Т.о., угловой коэффициент прямой 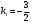 . Поскольку искомая прямая перпендикулярна прямой
. Поскольку искомая прямая перпендикулярна прямой 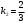 .
.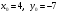 . Теперь по формуле (6)
. Теперь по формуле (6) 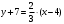 , или
, или 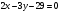 .
.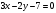 и
и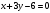 и отсекающей на оси абсцисс отрезок, равный 3.
и отсекающей на оси абсцисс отрезок, равный 3.
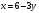 . Подставим в первое уравнение
. Подставим в первое уравнение 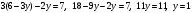 . Тогда
. Тогда 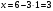 . Точка пересечения прямых имеет координаты
. Точка пересечения прямых имеет координаты 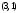 . По условию
. По условию 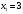 при
при 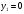 . Кроме того,
. Кроме того, 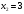 при
при 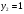 .
.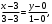 по свойству пропорции
по свойству пропорции 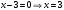 .
.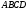 трапеция, если
трапеция, если 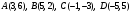 .
.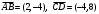 . Эти векторы коллинеарны, т.к. их координаты пропорциональны:
. Эти векторы коллинеарны, т.к. их координаты пропорциональны: 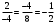 . Поэтому
. Поэтому 
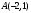 параллельно прямой
параллельно прямой 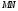 ,
,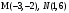 .
.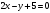 .
.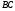 ,
,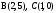 .
.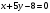 .
.