Статистика_Заказ_5239275_21_02_23. Решение. 1 В табл. 10. 1 представлен ранжированный ряд 1
 Скачать 49.96 Kb. Скачать 49.96 Kb.
|
|
Произвести статистическую обработку массива из n = 30 данных, содержащихся в столбцах №2, №3 и №4 таблицы 1. Таблица 1 №1 №2 №3 №4 №5 №6 №7 №8 №9 №10 __________________________________________________________ 561 555 569 555 567 559 567 555 566 557 580 568 560 572 563 574 542 562 542 572 564 560 569 543 560 565 568 558 539 550 566 563 562 546 570 582 568 565 561 554 548 558 586 562 559 553 567 553 572 567 550 562 557 564 582 576 567 554 567 550 534 574 560 561 578 543 544 567 576 550 567 546 571 570 560 546 566 578 581 555 576 572 542 567 566 548 578 539 550 551 556 540 557 548 540 577 576 548 553 573 и выполнить следующие задания: 1) составить ранжированный ряд, найти размах выборки и количество групп различных вариант; 2) составить точечный вариационный ряд; 3) преобразовать точечный вариационный ряд в интервальный с числом интервалов k = 8; 4) построить полигон относительных частот и гистограмму; 5) найти статистические характеристики выборки; 6) проверить гипотезу о нормальном распределении генеральной совокупности с помощью критерия Пирсона при числе степеней свободы s = 5 и уровне значимости α = 0,05; 7) найти доверительный интервал для математического ожидания генеральной совокупности с надежностью γ = 0,95. Решение. 1) В табл.10.1 представлен ранжированный ряд: Таблица 10.1
Размах R = 586 – 540 = 46; различных групп m = 21 Точечный вариационный ряд представим в виде табл.10.2 с указанием номера группы Таблица 10.2
Находим длину интервала h = 46/8 = 5,75 и формируем табл.10.3 Таблица 10.3
По данным табл.10.2 строим полигон относительных частот, который представлен на рис.10.1: Р  ис.10.1 ис.10.1П  о данным табл.3 строим гистограмму плотности частоты, представленной на рис.10.2: о данным табл.3 строим гистограмму плотности частоты, представленной на рис.10.2:Рис.10.2 5) Находим статистические характеристики выборки: Моды М(Х) = 560 и М(Х) = 562; медиана Ме(Х)= (561 + 562)/2 = 561,5; выборочные: средняя 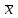 = 560,7; дисперсия = 560,7; дисперсия 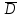 = 99,959; среднее квадратичное отклонение = 99,959; среднее квадратичное отклонение 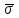 = 9,998. Как видно коэффициент вариации ( = 9,998. Как видно коэффициент вариации (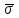 / /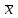 ) не превосходит 2%, что свидетельствует о том, что данные выборки не выходят за пределы первого класса точности расчетов. ) не превосходит 2%, что свидетельствует о том, что данные выборки не выходят за пределы первого класса точности расчетов.6) Находим для аргумента z функции Лапласа границы интервалов (zi, zi+1) в виде: zi = ( хi - 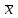 )/ )/ 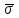 , zi+1 = ( хi+1 - , zi+1 = ( хi+1 - 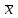 )/ )/ 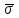 и заполняем табл.10.4 и заполняем табл.10.4Таблица 10.4
Находим теоретические вероятности pi и теоретические частоты niт = npi, заполняя табл.10.5 Таблица 10.5
Σ = 1 30 Вычисляем χ2набл , для чего формируем табл.10.6: Таблица 10.6
Σ = 7,817 38,624 Таким образом, χ2набл = 7,817. По таблицам критических точек χ2 при числе степеней свободы s = 5 и уровне значимости α = 0,05 определяем χ2кр =11,1 и, следовательно, имеем χ2набл < χ2кр. Вывод 1. Расхождение эмпирических и теоретических частот случайно (не значительно) и нулевую гипотезу о нормальном распределении генеральной совокупности принимаем. 7) Из соотношения 2Ф(t) = 0,95 по таблицам Лапласа находим аргумент t = 1,96. Тогда точность оценки при n = 30 и 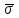 = 9,998 в соответствии с соотношением (10.7) составит δ = 3,578, а доверительный интервал ( = 9,998 в соответствии с соотношением (10.7) составит δ = 3,578, а доверительный интервал (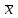 - 3,578; - 3,578; 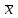 + 3,578) при + 3,578) при 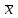 = 560,7 равен (557,122; 564,278). = 560,7 равен (557,122; 564,278).Вывод 2. В 95 случаях из 100 математические ожидания а различных выборок из данной генеральной совокупности не выйдут за границы доверительного интервала: 557,122 < а < 564,278. По критерию Вилкоксона проверим принадлежность к одной генеральной совокупности данных первого и второго столбцов таблицы. Решение. Сформулируем гипотезы: H0: F (x ) = G (x ) (выборочные совокупности однородны). H1: F (x ) ≠ G (x ) (выборочные совокупности неоднородны).
Найдем, какие места занимают в вариационном ряду, построенном по объединенной выборке, элементы выборки 2, назовем эти номера рангами элементов выборки 2 (строки выделены красным) и будем их складывать. Wэмп = 2 + 3 + 6 + 8 + 9 + 11 + 12 + 16 + 17 + 18 = 102. 1 подход. Wmin = m∙(m + 1)/2 = 10∙(10 + 1)/2 = 55. Wmax = mn + m∙(m + 1)/2 = 10∙10 + 10∙(10 + 1)/2 = 155. Wэмп = 102, 102∈[55; 155] и является симметричным относительно середины промежутка, поэтому можем сделать вывод о справедливости нулевой гипотезы H0, то есть принимаем гипотезу об однородности выборочных совокупностей. 2 подход. Выберем уровень значимости 0,01, тогда найдем по таблице критических значений критерия Вилкоксона: Wниж.крит (0,01/2; 10; 10) = 71; Wверх.крит = (m + n + 1)∙m − Wниж.крит = (10 + 10 + 1)∙10 – 71 = 139 Wэмп = 102, 102∈[71; 139], то есть принимаем нулевую гипотезу об однородности выборочных совокупностей. Контрольные вопросы. Определите понятие доверительной вероятности и доверительного интервала Доверительный интервал – интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения. Доверительная вероятность – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным. Оценивание с помощью доверительного интервала – способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала. Что такое точность и надежность оценки. Точность оценка характеризуется положительным числом δ, которое характеризует величину расхождения между оценками выборки и генеральной совокупности: |θ – θ*| < δ; δ > 0 Надежностью (доверительной вероятностью) оценки θ по θ* называют вероятность γ, с которой осуществляется неравенство |θ – θ*| < δ P(θ* - δ < θ < θ*+ δ) < γ В качестве параметров надежности наиболее часто используют величины, близкие к единице: 0,95; 0,99 и 0,999. 3. В чем суть проверки статистических гипотез и что лежит в основе критерия Пирсона. Статистическая гипотеза - это некоторое предположение о свойствах генеральной совокупности, которое необходимо проверить. Статистические гипотезы выдвигаются, когда необходимо проверить, является ли наблюдаемое явление элементом случайности или результатом воздействия некоторых мероприятий. Например, необходимо выяснить, значительно ли отличается средний объём продаж после проведения рекламной кампании от среднего объёма продаж после проведения рекламной кампании. Если ответ на этот вопрос положителен, то можно сделать вывод о том, что изменения являются результатом рекламной кампании. Выводы, полученные путём проверки статистических гипотез, носят вероятностный характер: они принимаются с некоторой вероятностью. Статистическая гипотеза может быть также предположением о свойствах двух совокупностей, если, например, в ходе мероприятий имело место воздействие только на одну совокупность и необходимо сделать вывод о том, было ли это воздействие результативным. Критерий χ2 Пирсона – это непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей). |

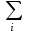 ni = 30
ni = 30