задачи по эконометрике. Решение а) Показывает если уровень технической оснащённости (х) увеличивается
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Задача 1. По группе 10 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости единицы продукции у (тыс. руб.) от уровня технической оснащённости х (тыс. руб.): 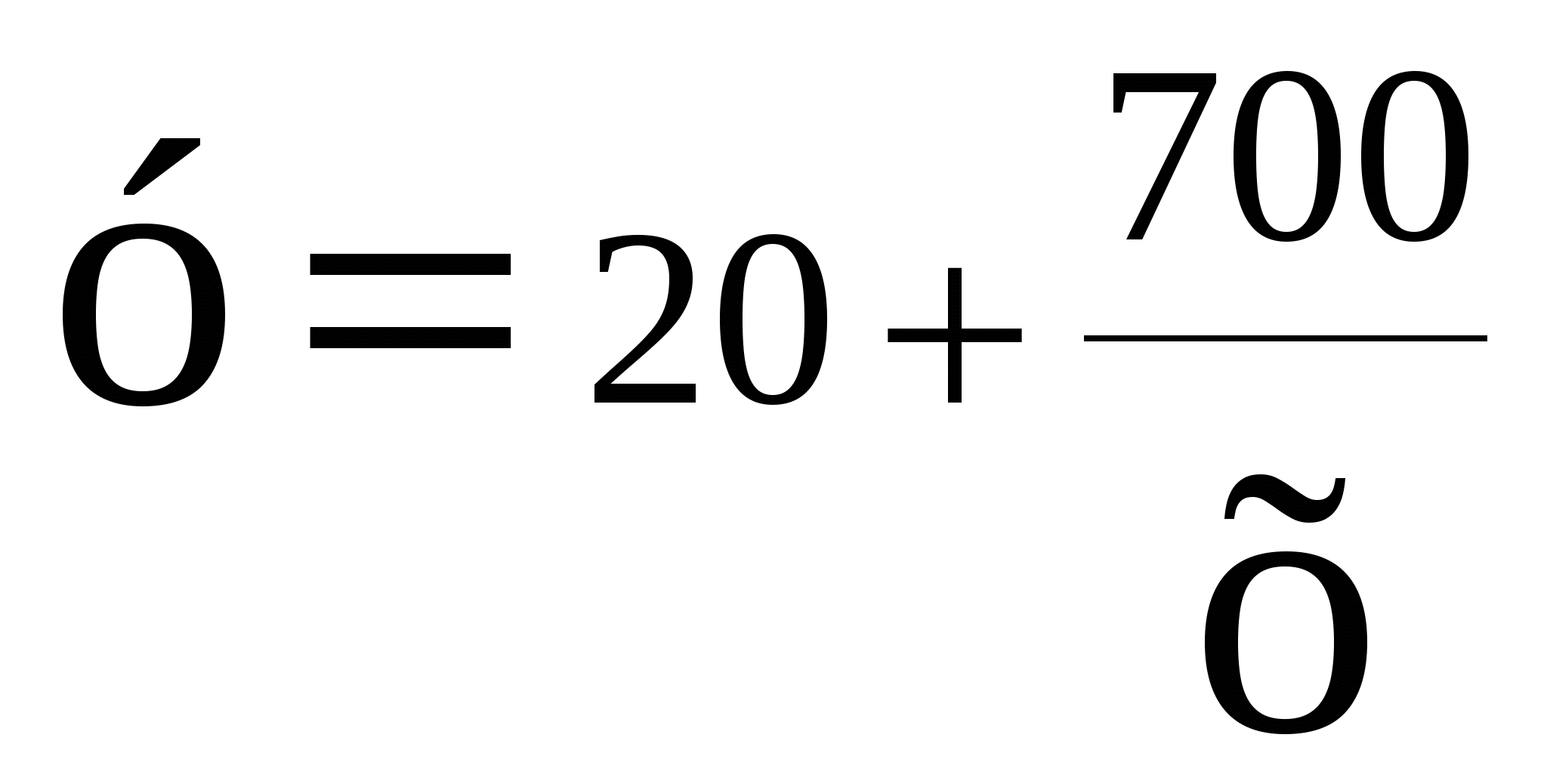 . Доля остаточной дисперсии в общей составила 0,19. . Доля остаточной дисперсии в общей составила 0,19.Задание Определите: а) коэффициент эластичности, предполагая, что стоимость активных производственных фондов составляет х=200 тыс. руб.; б) индекс корреляции; в) F – критерий Фишера. Сделайте выводы. Решение: а) Показывает если уровень технической оснащённости (х) увеличивается на 1 %, то себестоимости единицы продукции (у) уменьшается на 0,149 %. б) 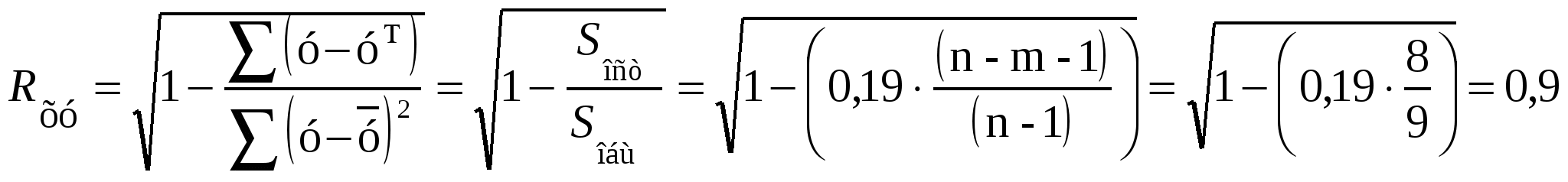 Связь между у и х сильная и прямая. 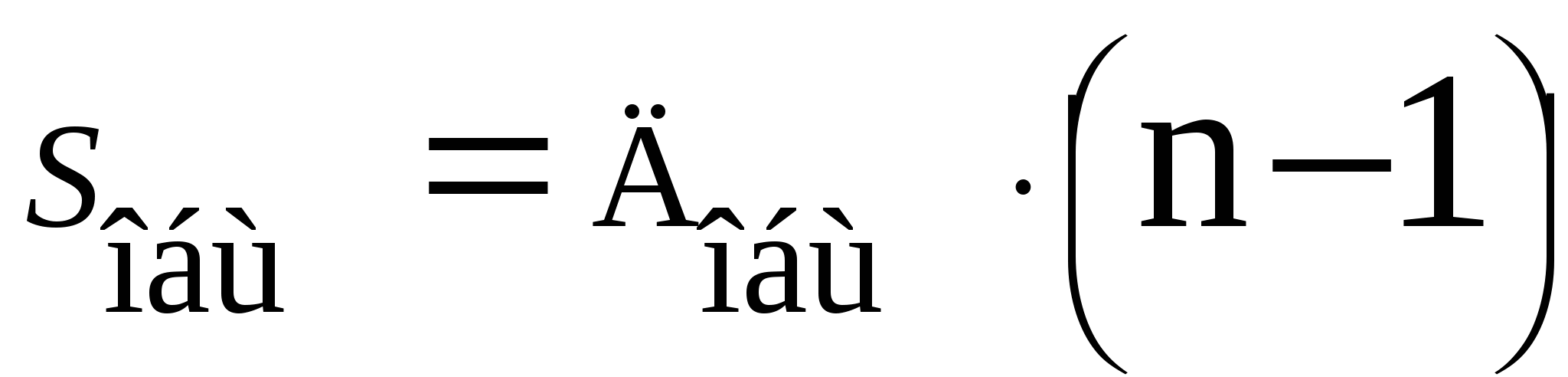 в) 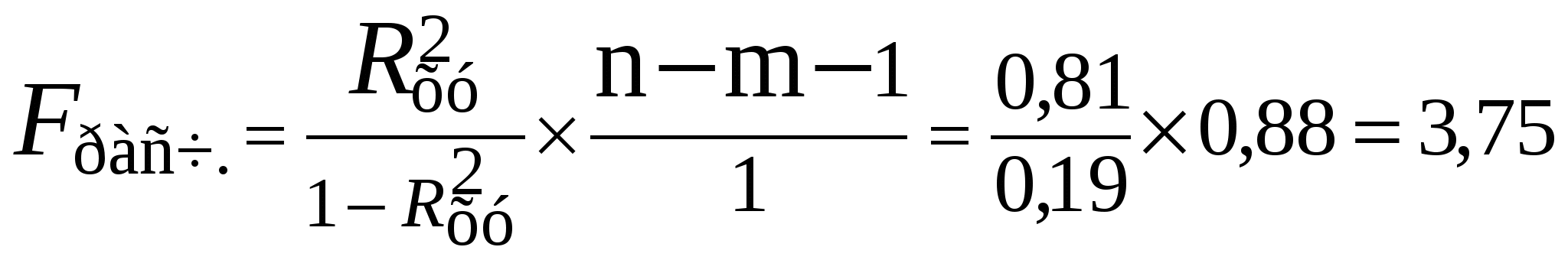 F табличное =4,96 Рассчитав F критерий Фишера увидим, что F табличное =4,96> F расчетное =3,75 следовательно линейная модель статистически незначима при α=0,05. Задача 2. Таблица 1. Показатели для расчёта линейной функции y=a+b·x 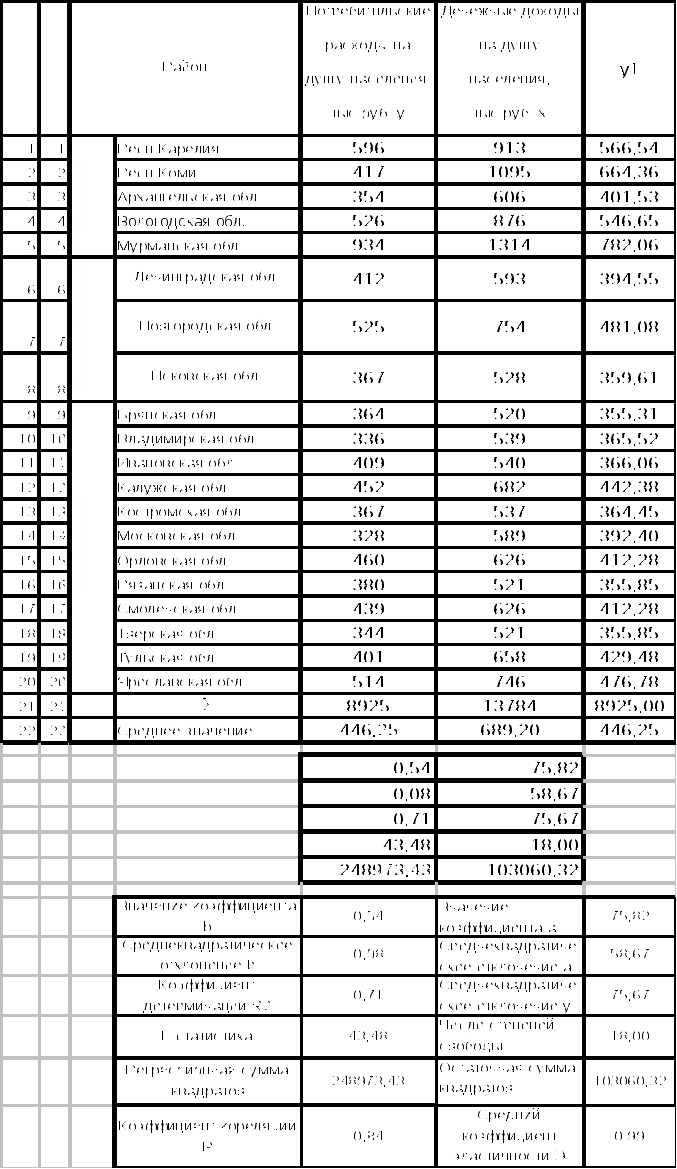 Рассчитав уравнение линейной функции видно, что если х увеличиться на 1 рубль, то у уменьшиться на 0,54 %. Коэффициент корреляции R показывает, что связь между х и у прямая 0,84% Коэффициент детерминации R2 показывает, что качество модели высокое и вариация результата у на 71% объясняется вариацией фактора х. Рассчитав F критерий Фишера увидим, что F табличное =4,41< F расчетное =43,48 следовательно линейная модель статистически значимая при α=0,05. Рассчитав среднюю ошибку аппроксимации видно, что в среднем расчетные значения отличаются от фактических на 9,86% точность построения модели невысокая и качество невысокое. Таблица 2. Показатели для расчёта степенной функции y=a·xb 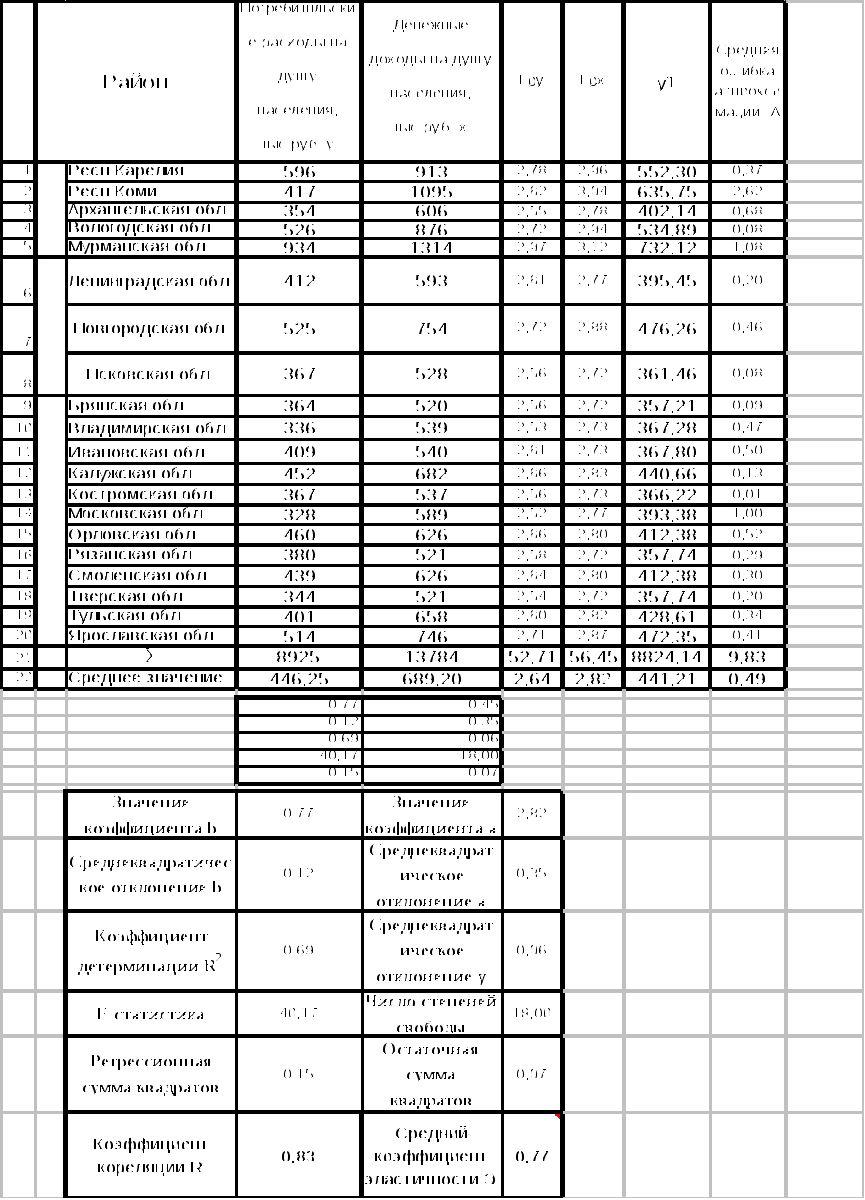 Рассчитав уравнение степенной функции видно, что если х увеличиться на 1%, то у уменьшиться на 0,77 %. Коэффициент корреляции R показывает, что связь между х и у прямая 0,83% Коэффициент детерминации R2 показывает, что качество модели высокое и вариация результата у на 69% объясняется вариацией фактора х. Рассчитав F критерий Фишера увидим, что F табличное =4,41< F расчетное =40,17 следовательно линейная модель статистически значимая при α=0,05. Рассчитав среднюю ошибку аппроксимации видно, что в среднем расчетные значения отличаются от фактических на 9,83% точность построения модели невысокая и качество невысокое. Таблица 3. Показатели для расчёта показательной функции y=a·bх 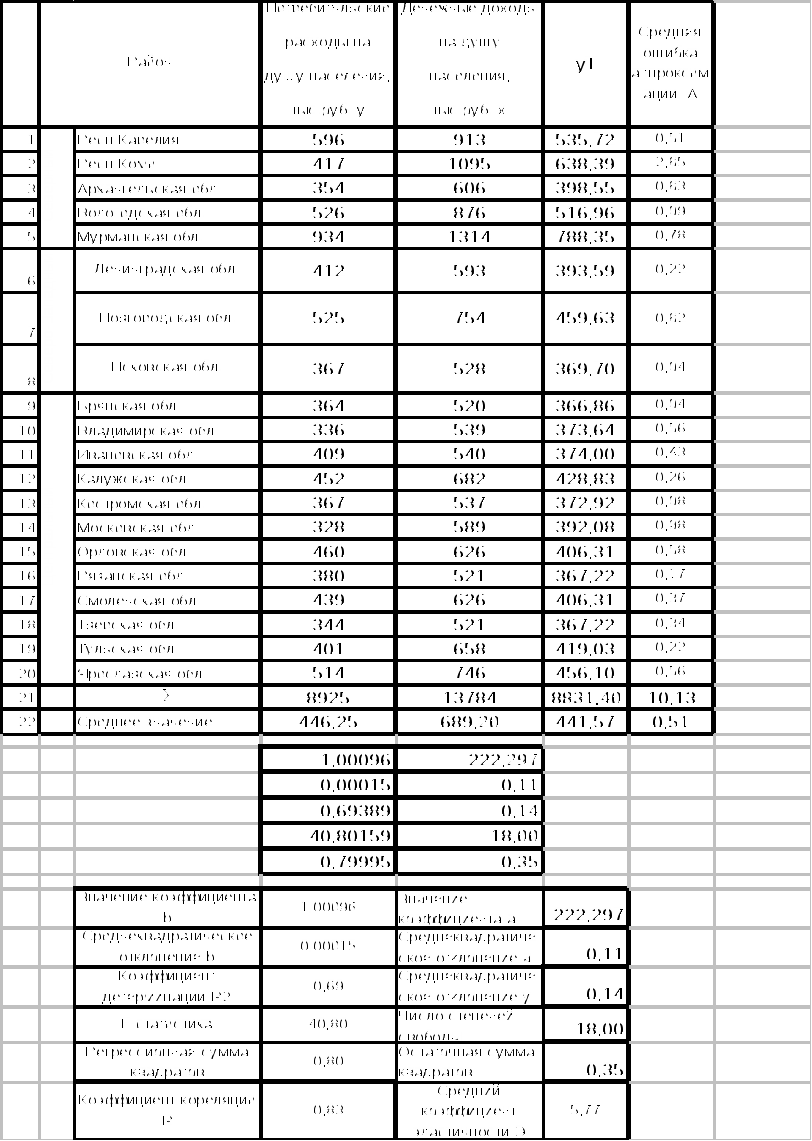 Рассчитав уравнение показательной функции видно, что если х увеличиться на 1 рубль, то у уменьшиться на 0,54 %. Коэффициент корреляции R показывает, что связь между х и у прямая 0,83% Коэффициент детерминации R2 показывает, что качество модели высокое и вариация результата у на 69% объясняется вариацией фактора х. Рассчитав F критерий Фишера увидим, что F табличное =4,41< F расчетное =40,80 следовательно линейная модель статистически значимая при α=0,05. Рассчитав среднюю ошибку аппроксимации видно, что в среднем расчетные значения отличаются от фактических на 10,13% точность построения модели невысокая и качество невысокое. Таблица 4. Сводная таблица уравнений парной регрессии.
В сводной таблице видно, что лучшей является степенная функция, но все рассчитанные модели являются статистически незначимыми из-за слабой связи х и у и малыми числами наблюдений. Таблица 5. Показатели для расчёта степенной функции упрогн= а∙хпрогнb при увеличении 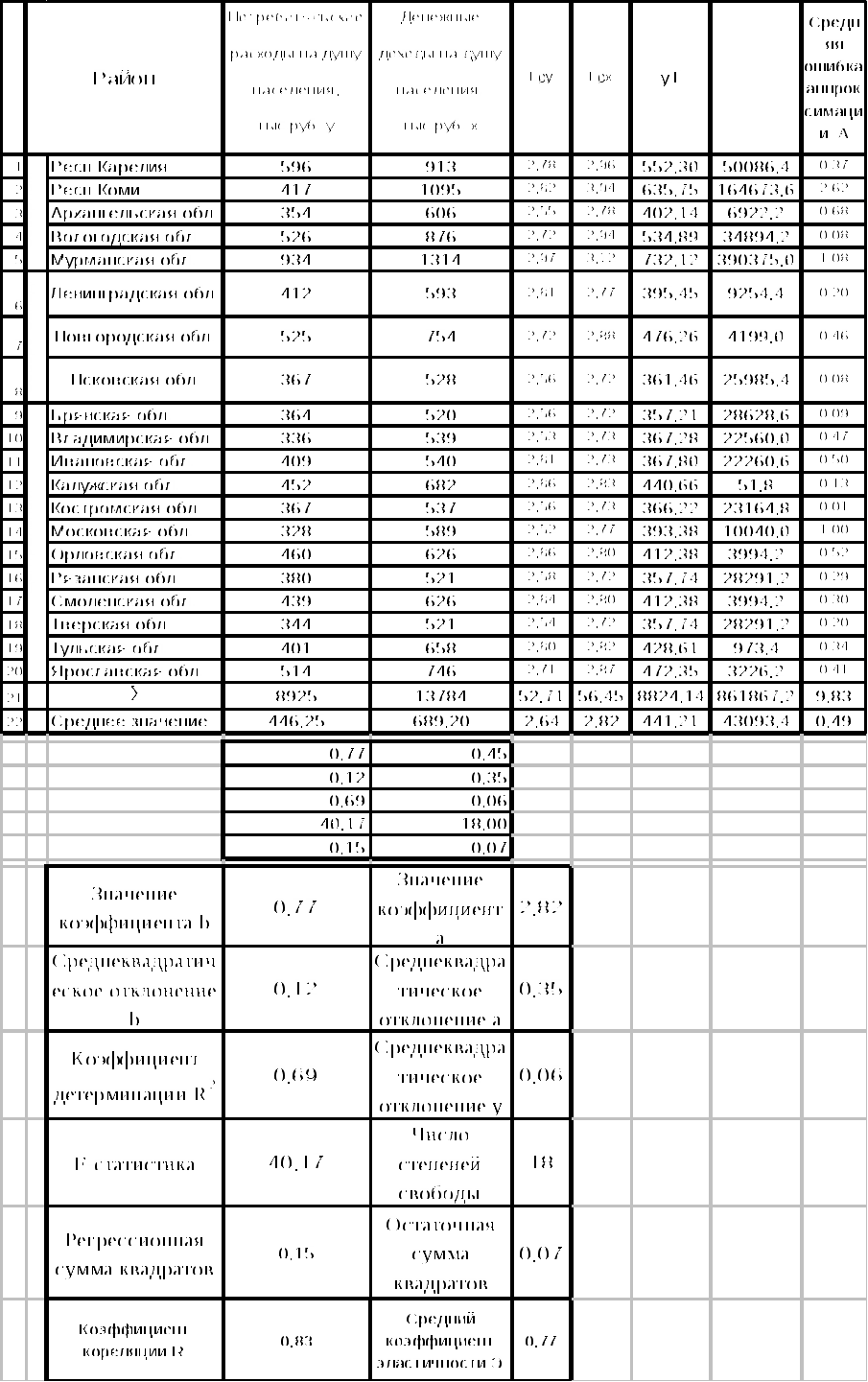 хпрогн= упрогн= а∙хпрогнb= 2,82∙716,770,77 = 445,5 Ттабл = 2,1009 при df = n-m-1=18, при α = 0,05 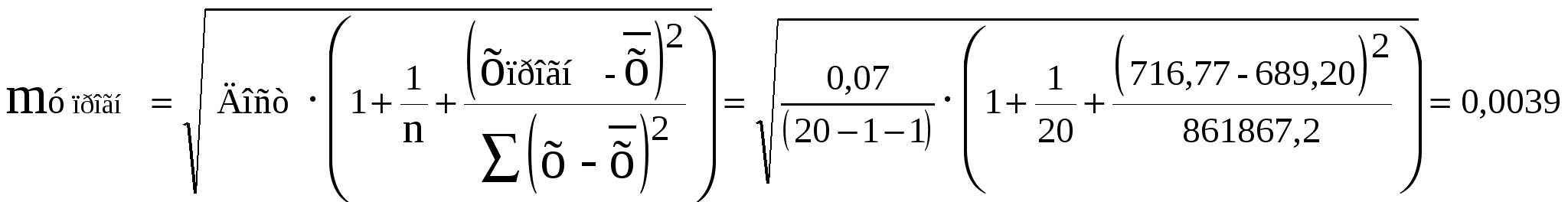 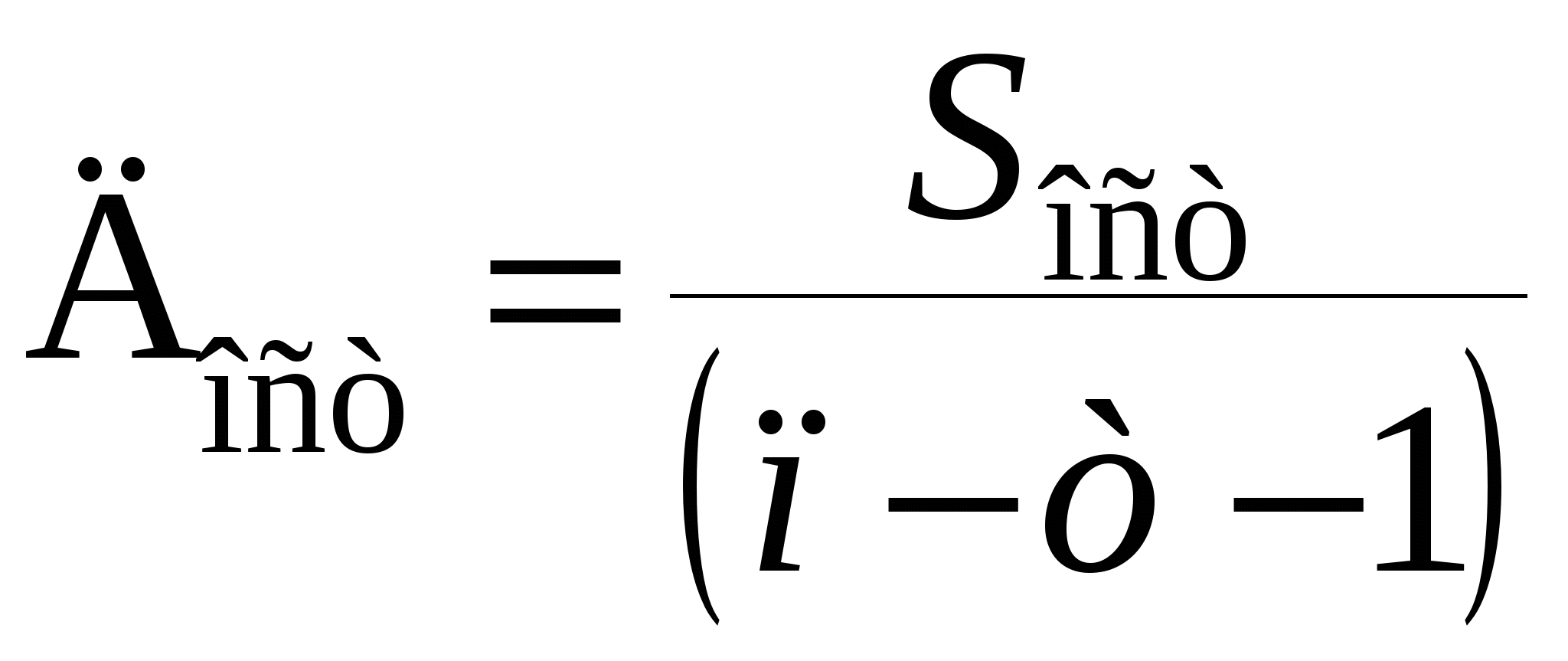 При увеличении х на 0,04 % результат у будет изменяться (увеличиваться ) от 445,49 до 445,6 Задача 3. Изучается зависимость по 30 предприятиям концерна изучается зависимость прибыли у (тыс. руб.) от выработки продукции на одного работника х1 (ед.) и индекса цен на продукцию х2 (%). Данные приведены в таблице.
Задание.
Решение: 1 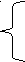 . у = а1 + b1х1 у = а + b2х2 . у = а1 + b1х1 у = а + b2х2∑ 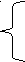 у = nа1 +b1∑ х1 ∑у = nа +b2∑ х2 у = nа1 +b1∑ х1 ∑у = nа +b2∑ х2∑ 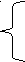 ху = а1∑ х1 +b1∑ х12 ∑ху = а∑ х2 +b2∑ х22 ху = а1∑ х1 +b1∑ х12 ∑ху = а∑ х2 +b2∑ х222 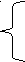 50 = 30а1 + 47b1 250 = 30а + 112b2 50 = 30а1 + 47b1 250 = 30а + 112b2 11750 = 47а1 + 2209b1 297 = 112а + 12544b2 8   ,33 = а1 + 1,56b1 8,33 = а + 3,7b2 ,33 = а1 + 1,56b1 8,33 = а + 3,7b2 250 = а1 + 47b1 2,65 = а + 112b2 - 241,7 = - 45,4b1 5,68 = - 108,3b2 b1 = а1 = 8,33 – 1,56(5,32) = 0,03 а = 8,33 – 3,7(- 0,05) = 8,51 у = 0.03 + 5.32х1 у = 8.51 – 0.05х2 Если х1 увеличится на 1 руб., то у увеличится на 5.32, если х2 увеличится на 1 руб., то у уменьшиться на 0,05. ]Коэффициенты корреляции rх1у= 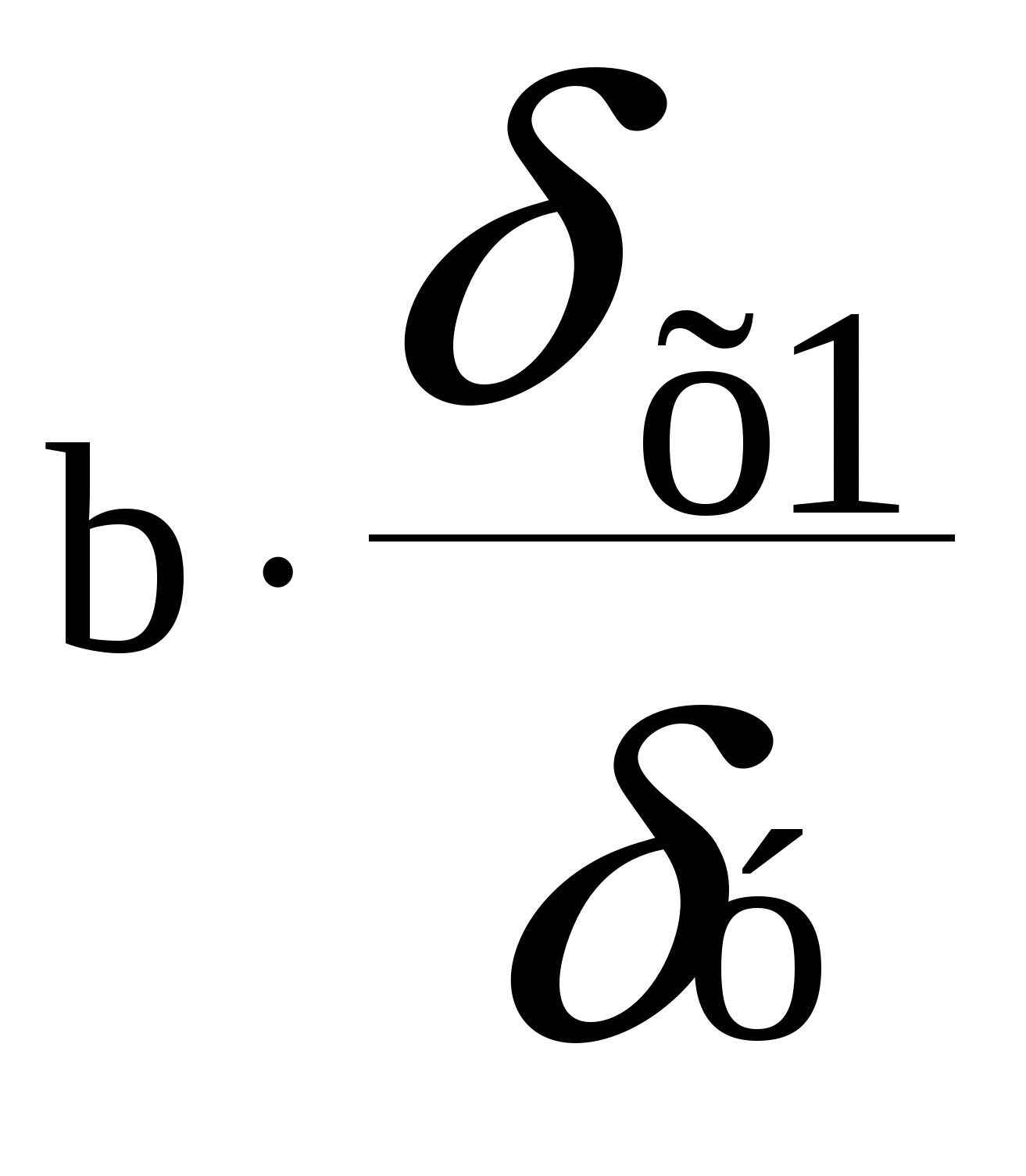 = =rх2у= 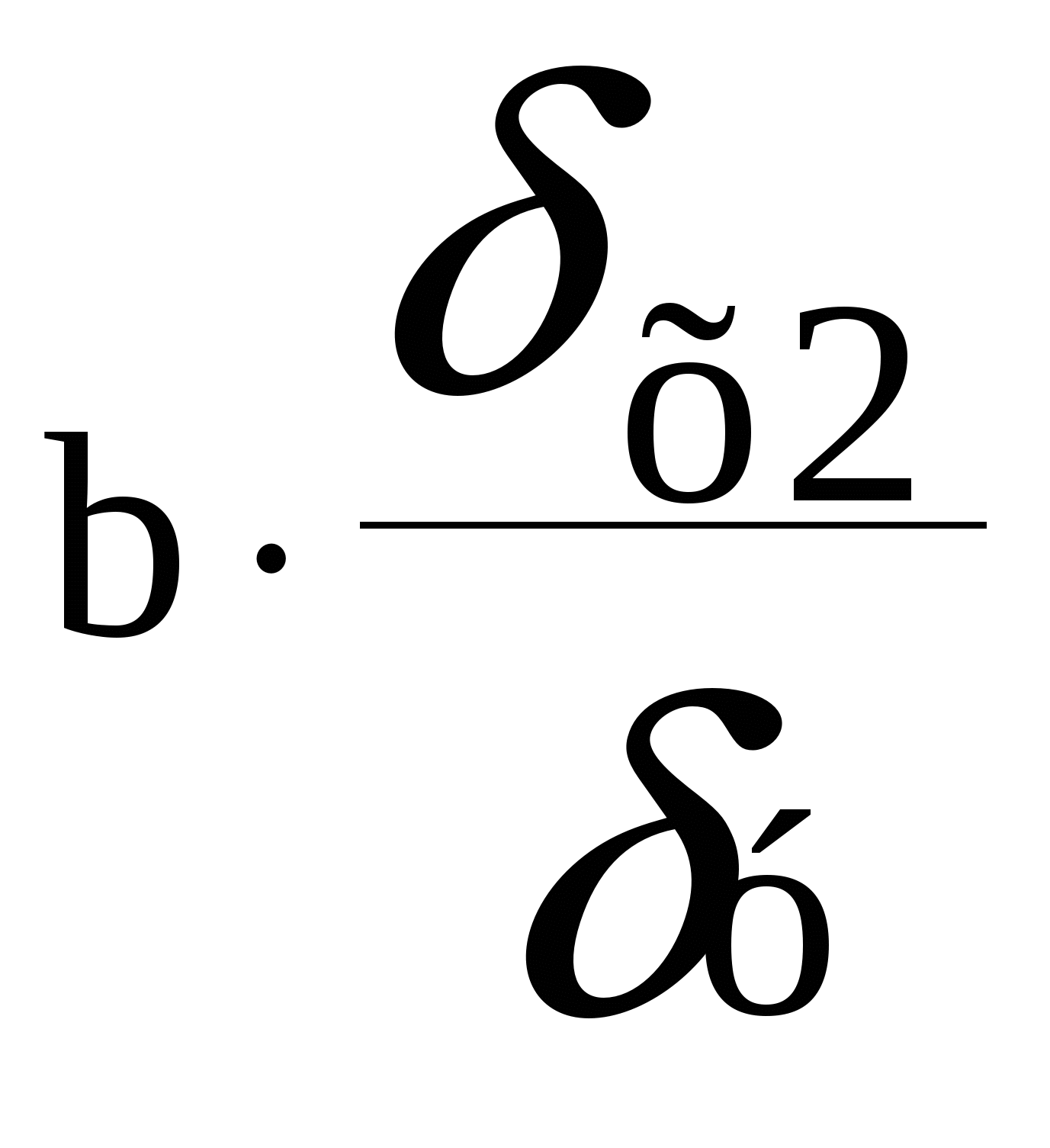 = =rх1у2=2,82 rх2у2=0,0009 Вариация результата у объясняется вариацией факторов х1 и х2, учтенных в модели, на долю х1 приходится 282 % от общей вариации у, а на долю х2 приходится 0,09 %. Fтабл. = 4,21 Fx1 Fтабл. фактор х1 нецелесообразно включать в модель. Fx2 Fтабл. фактор х2 нецелесообразно включать в модель. Следовательно линейная модель статистически незначима. 2.у = а + b1х1 + b2х2 bi = 1*y/xi b1 = 0.5*38/12 = 1.58 b2 = 0.41*38/21 = 0.74 а = 250-0.5*47-0,41*112 = 180.58 у = 180.58+0,5х1+0,41х2 Если х1 увеличится на 1 руб., то у увеличится на 0,5, если х2 увеличится на 1 руб., то у увеличится на 0,41. ty = 1tx1 + 2tx2 R  yx1 = 1 + Rx2x12 yx1 = 1 + Rx2x12Ryx2 = 1Rx1x2 + 2  0.68 = 1 + 0.422 0.63 = 0.421 + 2  1 = 0.68 - 0.422 1 = 0.68 - 0.4220.63 = (0.68 - 0.422)*0.42 + 2 0.63 = 0.2856 - 0.1762 + 2 0.63 = 0.2856 + 0.8242 2 = (0.63 – 0.2856)/0.824 2 = 0.41 1 = 0.68 - 0.42*0.41 1 = 0.5 ty = 0.5tx1 + 0.41tx2 Если х1 увеличится на 1, то у увеличится на 0,5 если х2 увеличится на 1, то у увеличится на 0,41. х2 сильнее влияет на у, чем х1.
R2yx1x2 = 0.772 = 0.59 Зависимость у от х1, х2 тесная, в ней 59 % вариации у объясняется вариацией факторов, учтенных в модели, на долю прочих факторов, не включенных в модель приходится 41 % от общей вариации у. 4. 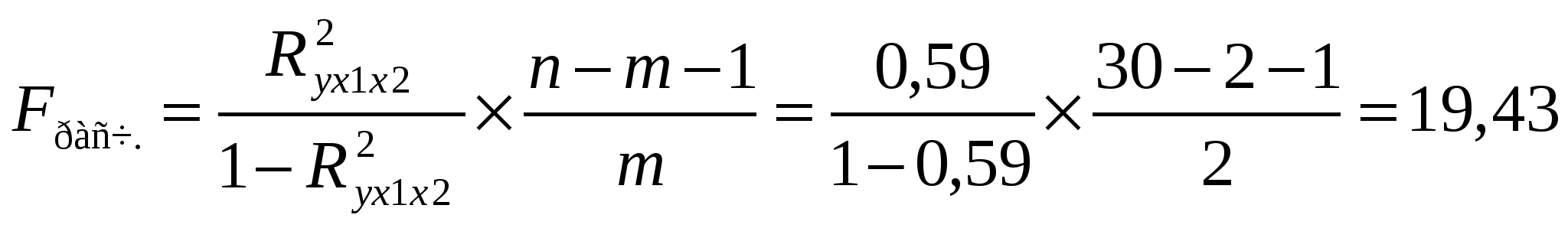 Fтабл. = 3,35 Fрасч. Fтабл. уравнение множественной регрессии статистически значимо. 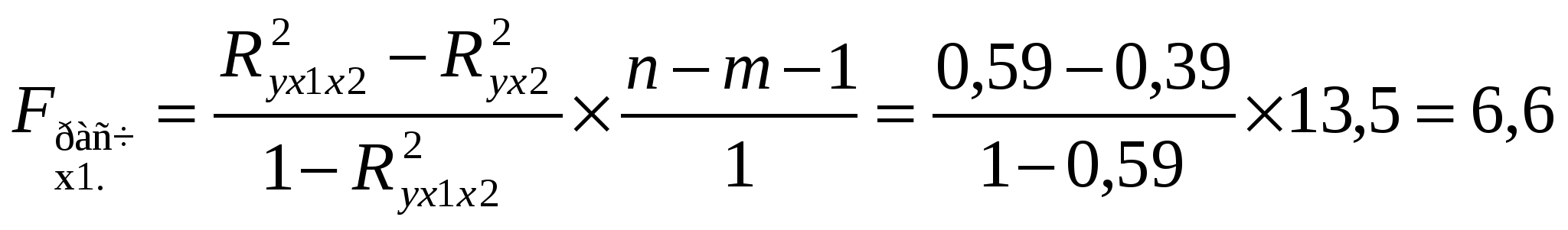 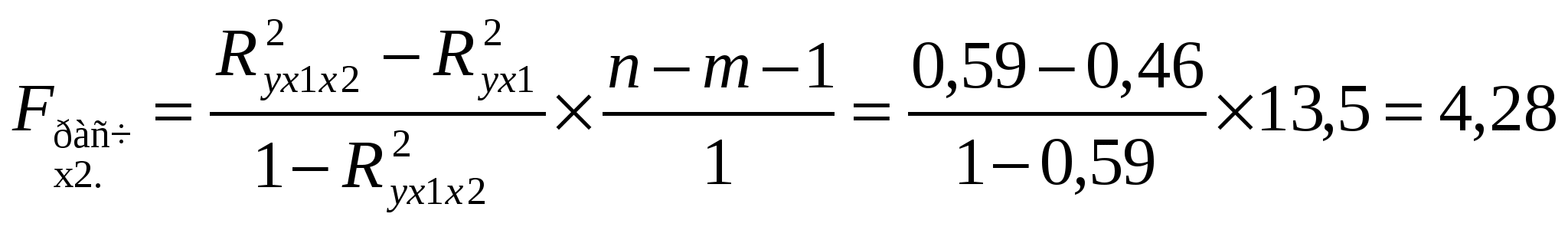 Fтабл. = 4,21 Fx1 Fтабл. фактор х1 целесообразно включать в модель т.к. он увеличивает качество модели Fx2 Fтабл. фактор х2 увеличивает качество модели его необходимо включать в уравнение. Литература 1. Эконометрика: Учебник под ред. И.И.Елисеевой, М: «Финансы и статистика», 2001; 2. «Практикум по эконометрике» под ред. И.И.Елисеевой, М: «Финансы и статистика», 2001; 3. Мхитарян, Айвазян «Прикладная статистика и основы эконометрики». М: Юнити, 1998; 4. Магнус Л.Р., Катышев П.К., Пкрсецкий А.А. «Эконометрика. Начальный курс: учебник». М: Дело, 2001; 5. К.Доугерти. «Введение в эконометрику». М: Инфра-М. Норма, 1999. |
