Высшая математика. Решение а решить систему по правилу Крамера Запишем систему в виде a
 Скачать 298.51 Kb. Скачать 298.51 Kb.
|
1 2 Задание № 2. Даны координаты вершин пирамиды 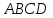 . Требуется: . Требуется:а) найти длину ребра 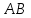 ; ;б) найти косинус угла между ребрами 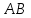 и и 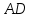 ; ;в) найти синус угла между ребром 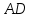 и плоскостью и плоскостью 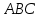 ; ;г) найти площадь треугольника 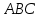 ; ;д) найти объем пирамиды 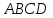 и длину высоты, опущенную из вершины и длину высоты, опущенную из вершины 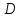 на плоскость на плоскость 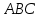 ; ;е) записать уравнение плоскости 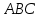 и уравнение высоты, опущенной из вершины и уравнение высоты, опущенной из вершины 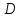 на плоскость на плоскость 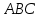 . .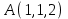 , , 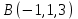 , , 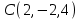 , , 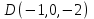 . .Решение. а) найти длину ребра 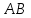 ; ;Длина вектора a(X;Y;Z) выражается через его координаты формулой: б) найти косинус угла между ребрами 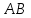 и и 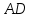 ; ;Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле: где a1a2 = X1X2 + Y1Y2 + Z1Z2 Найдем угол между ребрами AB(-2;0;1) и AD(-2;-1;-4): γ = arccos(0) = 90.0030 в) найти синус угла между ребром 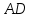 и плоскостью и плоскостью 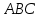 ; ;Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 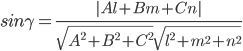 Уравнение плоскости ABC: 3x + 5y + 6z-20 = 0 Уравнение прямой AD: γ = arcsin(0.913) = 65.925o г) найти площадь треугольника 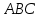 ; ;Площадь грани можно найти по формуле: где Найдем площадь грани ABC Найдем угол между ребрами AB(-2;0;1) и AC(1;-3;2): Площадь грани ABC д) найти объем пирамиды 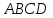 и длину высоты, опущенную из вершины и длину высоты, опущенную из вершины 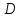 на плоскость на плоскость 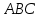 ; ;Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
Находим определитель матрицы ∆ = (-2)*((-3)*(-4)-(-1)*2)-1*(0*(-4)-(-1)*1)+(-2)*(0*2-(-3)*1) = -35 Длина высоты пирамиды, проведенной из вершины D(-1,0,-2) Расстояние d от точки M1(x1;y1;z1) до плоскости Ax + By + Cz + D = 0 равно абсолютному значению величины: 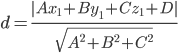 Уравнение плоскости ABC: 3x + 5y + 6z-20 = 0 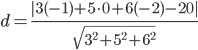 е) записать уравнение плоскости 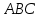 и уравнение высоты, опущенной из вершины и уравнение высоты, опущенной из вершины 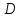 на плоскость на плоскость 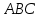 . .сли точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
Уравнение плоскости ABC
(x-1)(0*2-(-3)*1) - (y-1)((-2)*2-1*1) + (z-2)((-2)*(-3)-1*0) = 3x + 5y + 6z-20 = 0 Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: Уравнение плоскости ABC: 3x + 5y + 6z-20 = 0 Задание № 3. Вычислить пределы:
Решение. 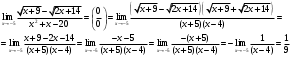 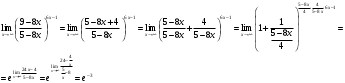 Задание № 4. Найти 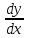 для функций: для функций:
Решение. А) 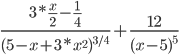 = = 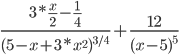 Производную этого выражения находим по формуле: (xn)' = n xn-1 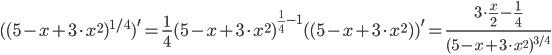 (5-x+3x2)' = (-x)' + (3x2)' + (5)' = (-1) + 6x = 6x-1 Здесь: (3x2)' = 32x2-1(x)' = 6x (x)' = 1 Ответ: 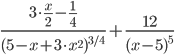 Б) Поскольку функция задана в неявном виде, то производную ищем по формуле: 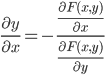 Для нашей функции: Тогда: 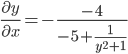 или илиЗадание № 5. Исследовать функцию и построить ее график. 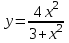 . . Решение. 1) ОДЗ 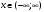 2) Поскольку f(-x)=f(x), то функция является четной. 3) Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: Находим коэффициент k: Находим коэффициент b: Получаем уравнение горизонтальной асимптоты: y = 4 4) Находим интервалы возрастания и убывания. Первая производная. или Находим нули функции. Для этого приравниваем производную к нулю 24x = 0 Откуда: x1 = 0
В окрестности точки x = 0 производная функции меняет знак с (-) на (+). Следовательно, точка x = 0 - точка минимума. 5) Найдем интервалы выпуклости и вогнутости функции. Вторая производная. или Находим корни уравнения. Для этого полученную функцию приравняем к нулю. Откуда точки перегиба: x1 = -1 x2 = 1
График функции 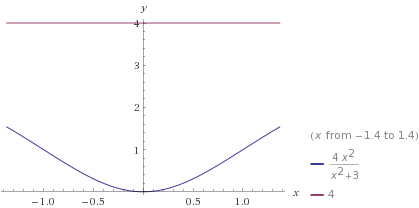 Задание № 6. Найти неопределенные интегралы.
Формула интегрирования по частям: Положим dV= dx Тогда: V = x Поэтому: Находим интеграл Ответ: Б) 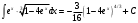 Задание № 7. С помощью определенного интеграла вычислить площадь области 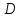 , ограниченной заданными линиями. , ограниченной заданными линиями.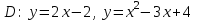 . .Решение. Построим область 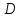 , ограниченную заданными линиями. , ограниченную заданными линиями.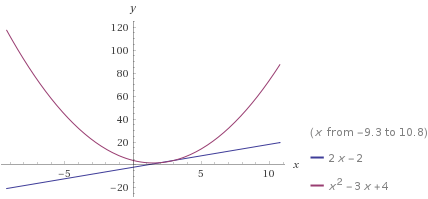 Н  айдем точки пересечения параболы и прямой для этого решим следующую систему уравнений: айдем точки пересечения параболы и прямой для этого решим следующую систему уравнений: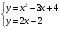 При решении квадратного уравнения системы x2-5x+6=0, получаем два корня х1=2, х2=3 , которые являются координатами концов промежутка интегрирования для разности функций f1(x)= x2-3x+4, f2(x)=2x-2 (т.к. прямая лежит выше параболы в рассматриваемой области). В результате вычислений получаем: 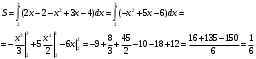 площадь области S=1/6(ед2). Список литературыКонспект лекций по высшей математике: полный курс. Д.Т. Письменный. М.: Айрис-пресс. 2009. Курс высшей математики. Введение в математический анализ. Дифференциальное исчисление. Под ред. И.М. Петрушко. Лекции и практикум (учебное пособие) Лань, 2008. Линейная алгебра и геометрия. А.И. Кострикин, Ю.И. Манин. Лань, 2008. Дифференциальное и интегральное исчисление. Т.1 Н.С. Пискунов, М. Интеграл-пресс. 2007. Сборник задач по математике для втузов. Ч.1,2. Под ред. А.В. Ефимова и А.С. Поспелова, М., ФМ, 2004. Практическое руководство к решению задач по высшей математике. (линейная алгебра, векторная алгебра, аналитическая геометрия, математический анализ), Лань, 2007. 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

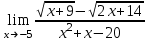 ,
,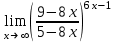 .
.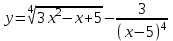 ,
,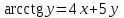 ,
,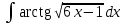 ,
,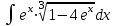 ,
,