типовой расчет. Решение дифференциальных уравнений а б в г
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Вариант 20. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 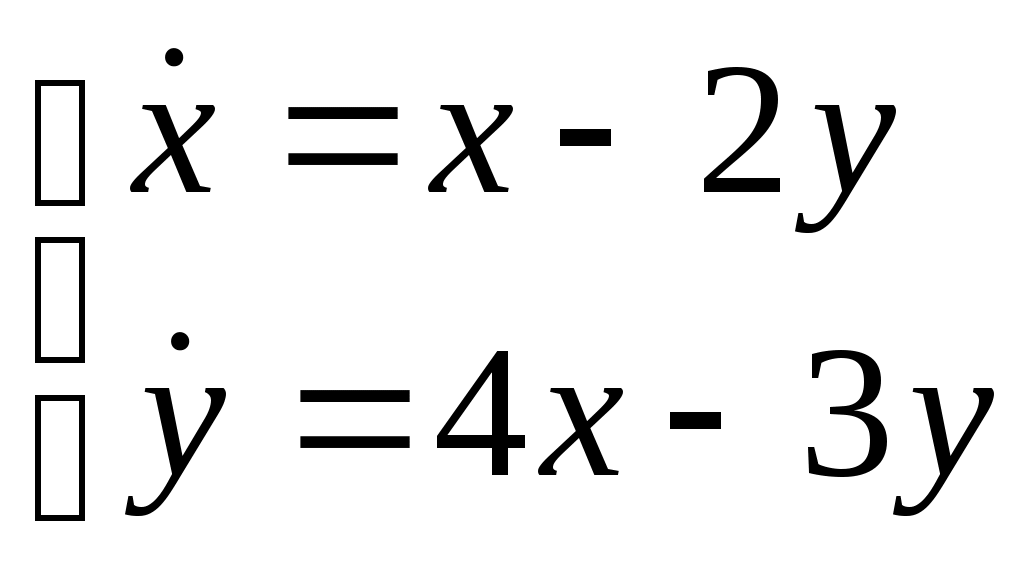 . . Найти уравнение кривой, проходящей через т. A(1, 2) и обладающей тем свойством, что отрезок, отсекаемый на оси ординат любой касательной, равен абсциссе точки касания. Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных Вариант 21. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 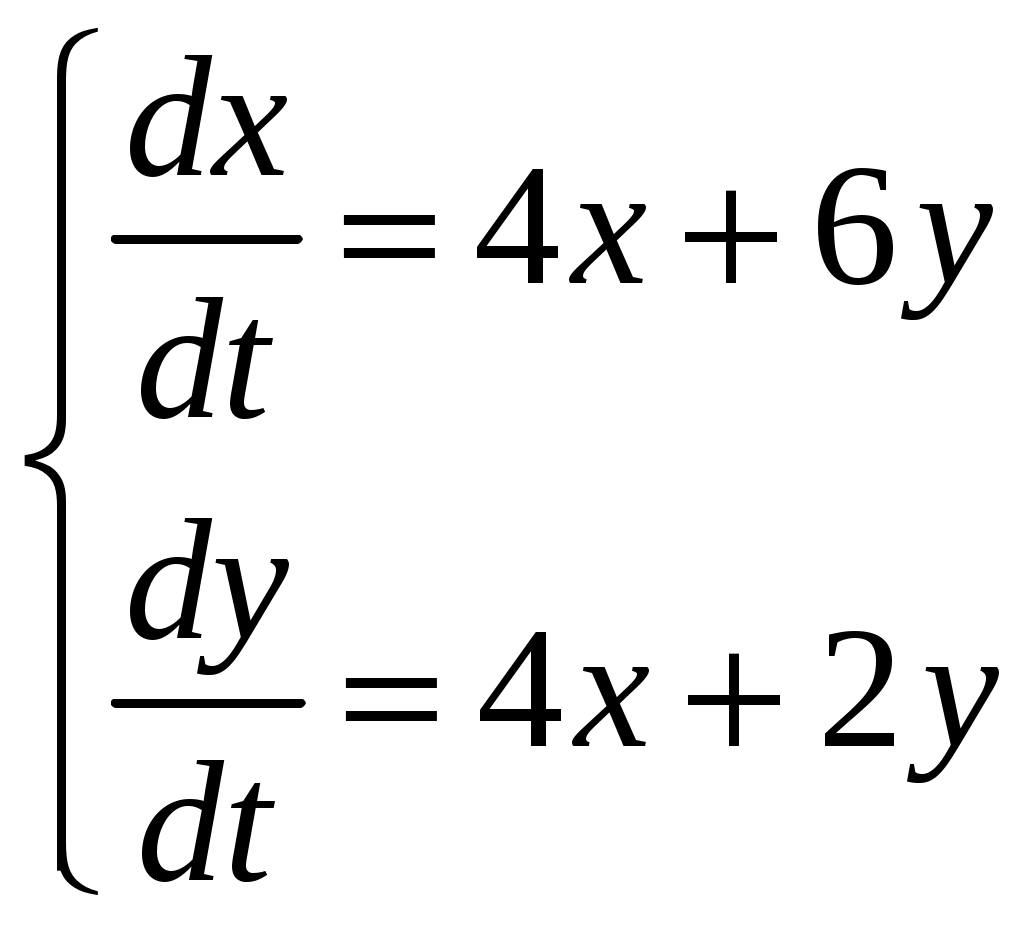 . . Тело массой Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных Вариант 22. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 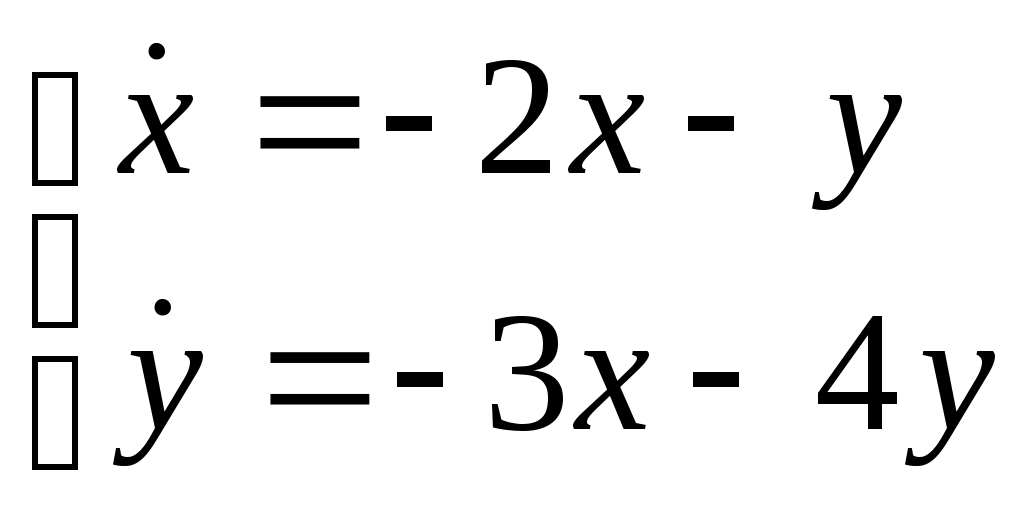 . . Найти уравнение кривой, проходящей через т. A(-1,-1) и обладающей тем свойством, что отрезок, отсекаемый на оси абсцисс касательной, проведенной в любой точке кривой, равен квадрату абсциссы точки касания. Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных Вариант 23. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 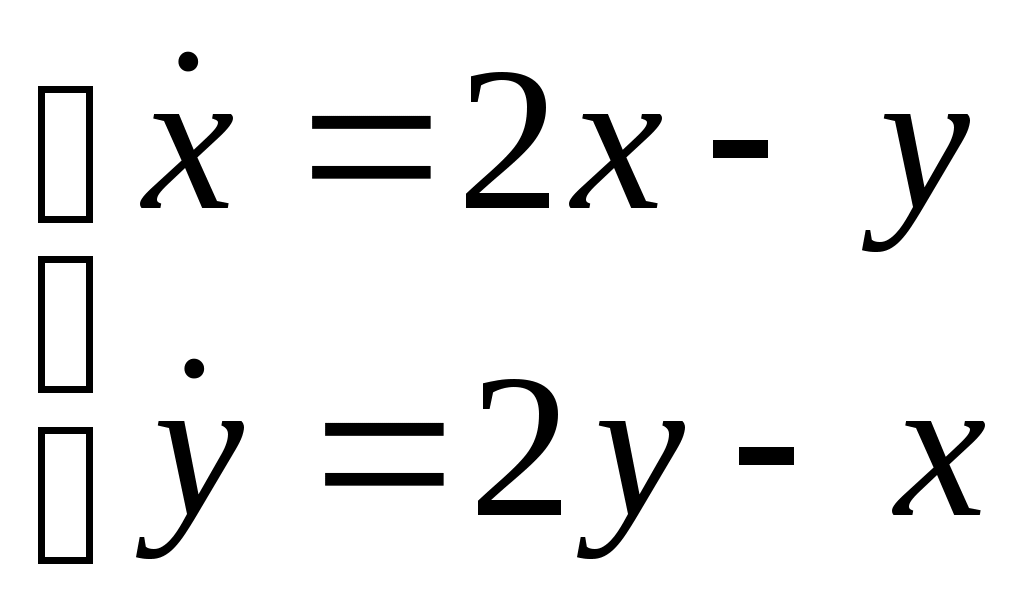 . . Материальная точка массой Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных Вариант 24. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 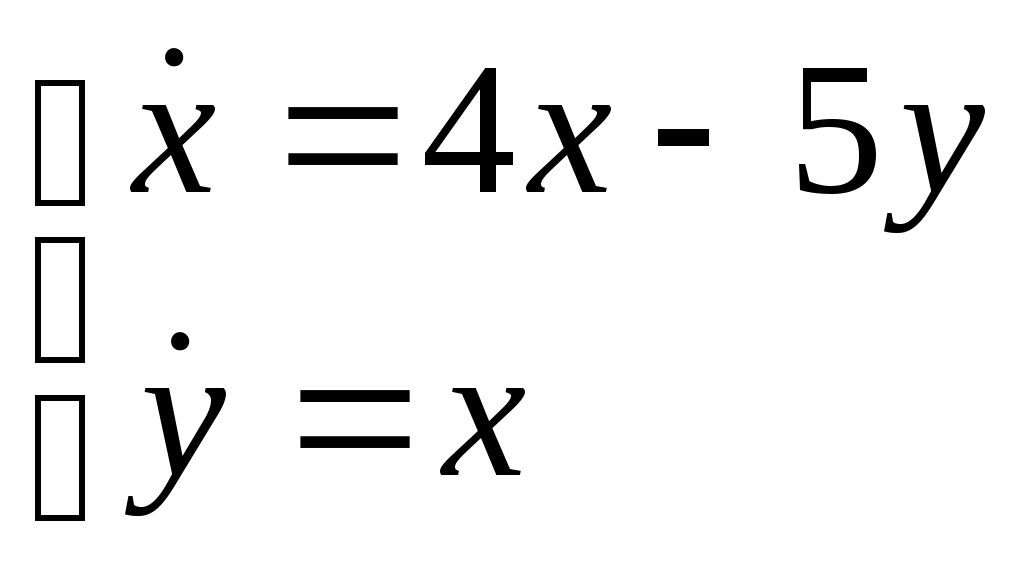 . . На тело массой Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных Вариант 25. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 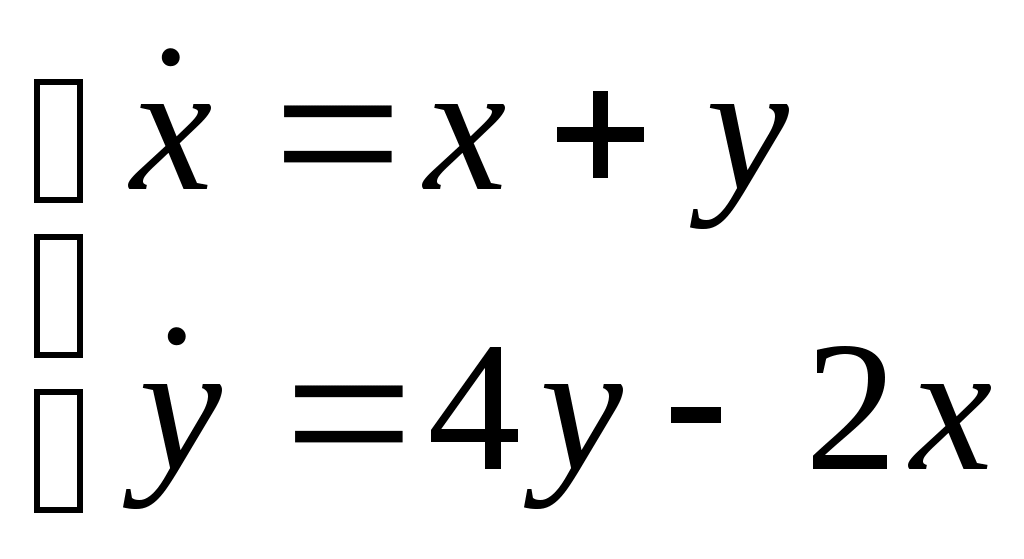 . . Найти уравнение кривой, проходящей через точку A(17, 17) и обладающей тем свойством, что отрезок, отсекаемый на оси ОХ касательной, проведенной в любой точке кривой, равен кубу абсциссы точки касания. Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных Вариант 26. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 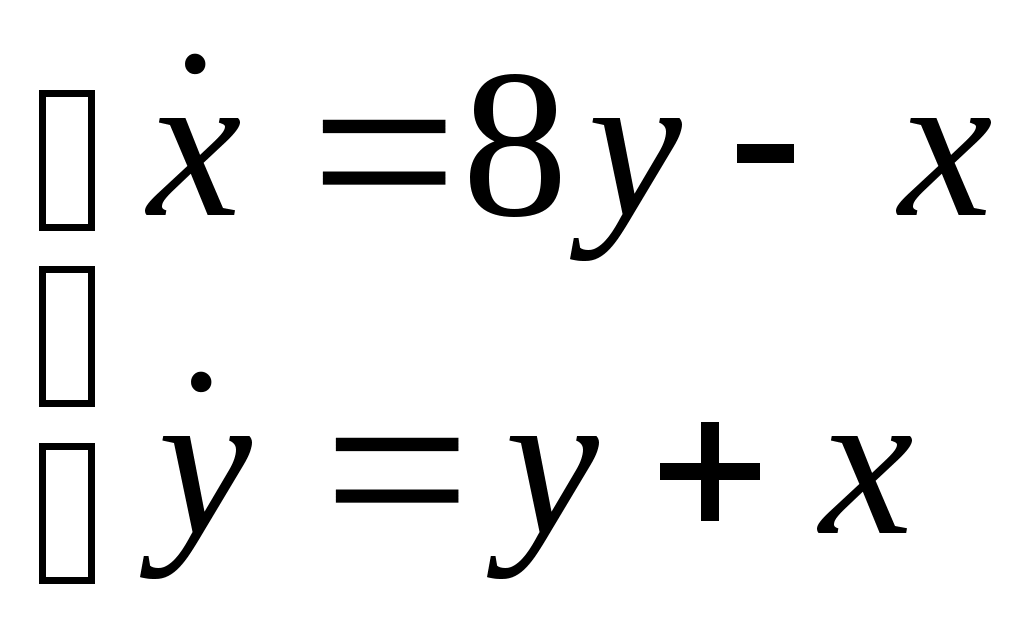 . . Найти уравнение кривой, проходящей через точку B(1, 3) и обладающей тем свойством, что отрезок, отсекаемый на оси ОУ любой касательной, равен удвоенной абсциссе точки касания. Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных Вариант 27. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 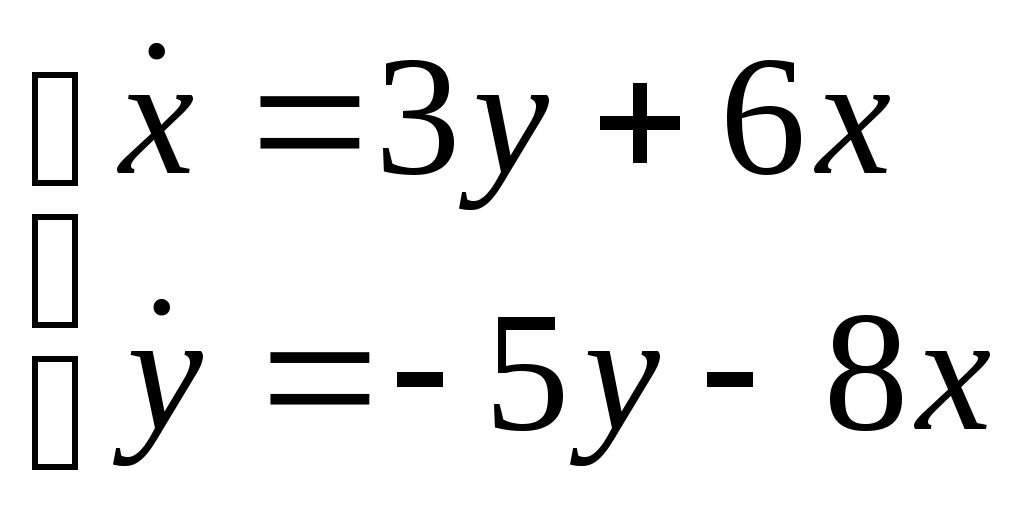 . . Найти уравнение кривой, проходящей через точку A(2, 0 ) и обладающей тем свойством, что отрезок, отсекаемый на оси ОУ любой касательной, равен удвоенной абсциссе точки касания. Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных Вариант 28. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 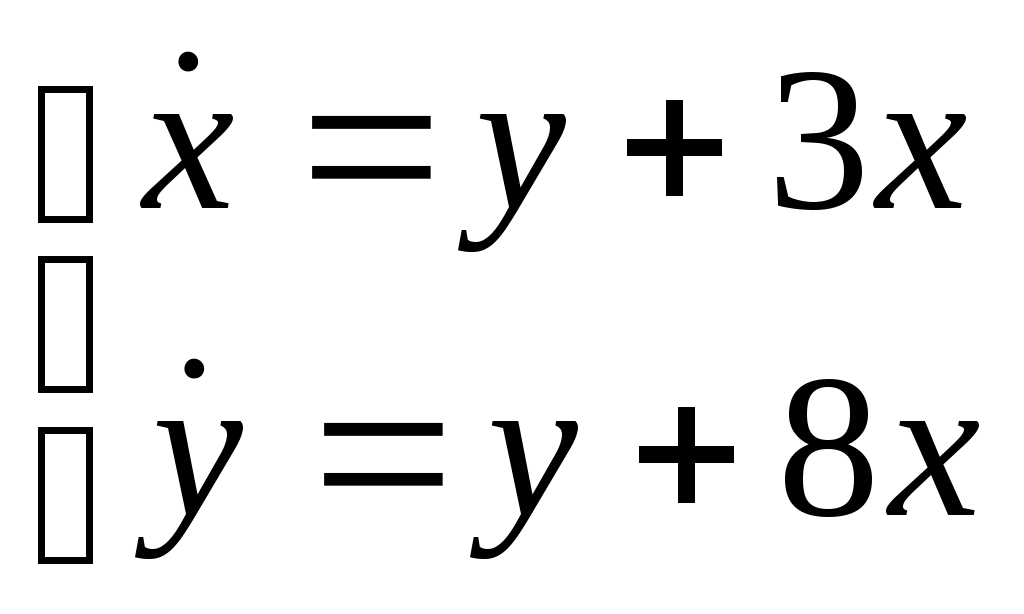 . . Найти уравнение кривой, проходящей через точку B(9, 1) и обладающей тем свойством, что отрезок любой касательной, заключенный между точкой касания и осью ОХ, делится пополам осью ОУ. Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных Вариант 29. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 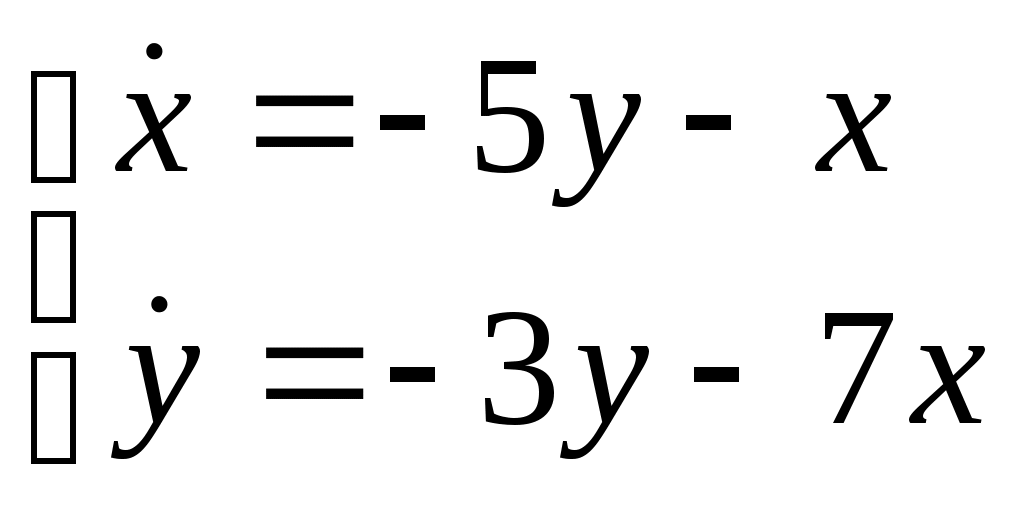 . . Найти уравнение кривой, проходящей через точку B(16, 1) и обладающей тем свойством, что угловой коэффициент любой касательной вдвое меньше углового коэффициента радиус-вектора точки касания. Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных Вариант 30. Найти общее решение дифференциальных уравнений:
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям Найти общее решение системы дифференциальных уравнений 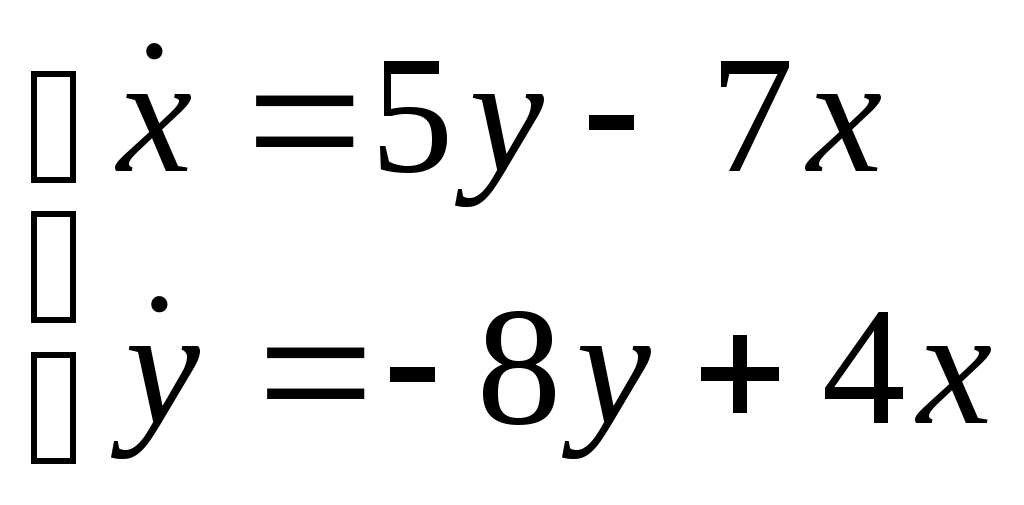 . . Моторная лодка движется в спокойной воде со скоростью Найти общее решение дифференциального уравнения Найти общее решение дифференциального уравнения методом вариации произвольных постоянных |
