Контрольная по математике 10 вариант теория вероятностей. Математика теория вероятностей. Решение. Для удобства оформим данные задачи в таблице. Вид глины

• Название: Решение. Для удобства оформим данные задачи в таблице. Вид глины
• Анкор: Контрольная по математике 10 вариант теория вероятностей
• Дата: 10.06.2021
• Размер: 135.5 Kb.
• Имя файла: Математика теория вероятностей.doc
• Тип: Решение; #216541

Контрольная работа по математике

Вариант 10
Задача 1. Кирпичный завод выпускает кирпичи двух марок (М1 и М2). Для производства кирпича применяется глина трех видов. Нормы расхода глины каждого вида на 1 кирпич первой марки равны 4, 2, 1 условных единиц; на 1 кирпич второй марки - 2, 3, 4 усл.ед. Общие запасы глины А, В и С составляют 32, 32, 36 усл.eд. Прибыль от реализации 1 кирпича первой марки 5 усл.ед.(в руб.), а второй марки – 8 условных единиц. Составить план производства, обеспечивающий максимальную прибыль.

Решение.

Для удобства оформим данные задачи в таблице.

Вид глины	Нормы расхода глины (усл.ед.) на один кирпич		Общие запасы глины (усл.ед.)
	М1	М2
А	4	2	32
В	2	3	32
С	1	4	36
Прибыль (руб.)	5	8

х₁ – количество кирпича вида М1, планируемого к выпуску;

x₂ – количество кирпича вида М2, планируемого к выпуску.

2. Зададим целевую функцию:

.

3. Составим систему ограничений: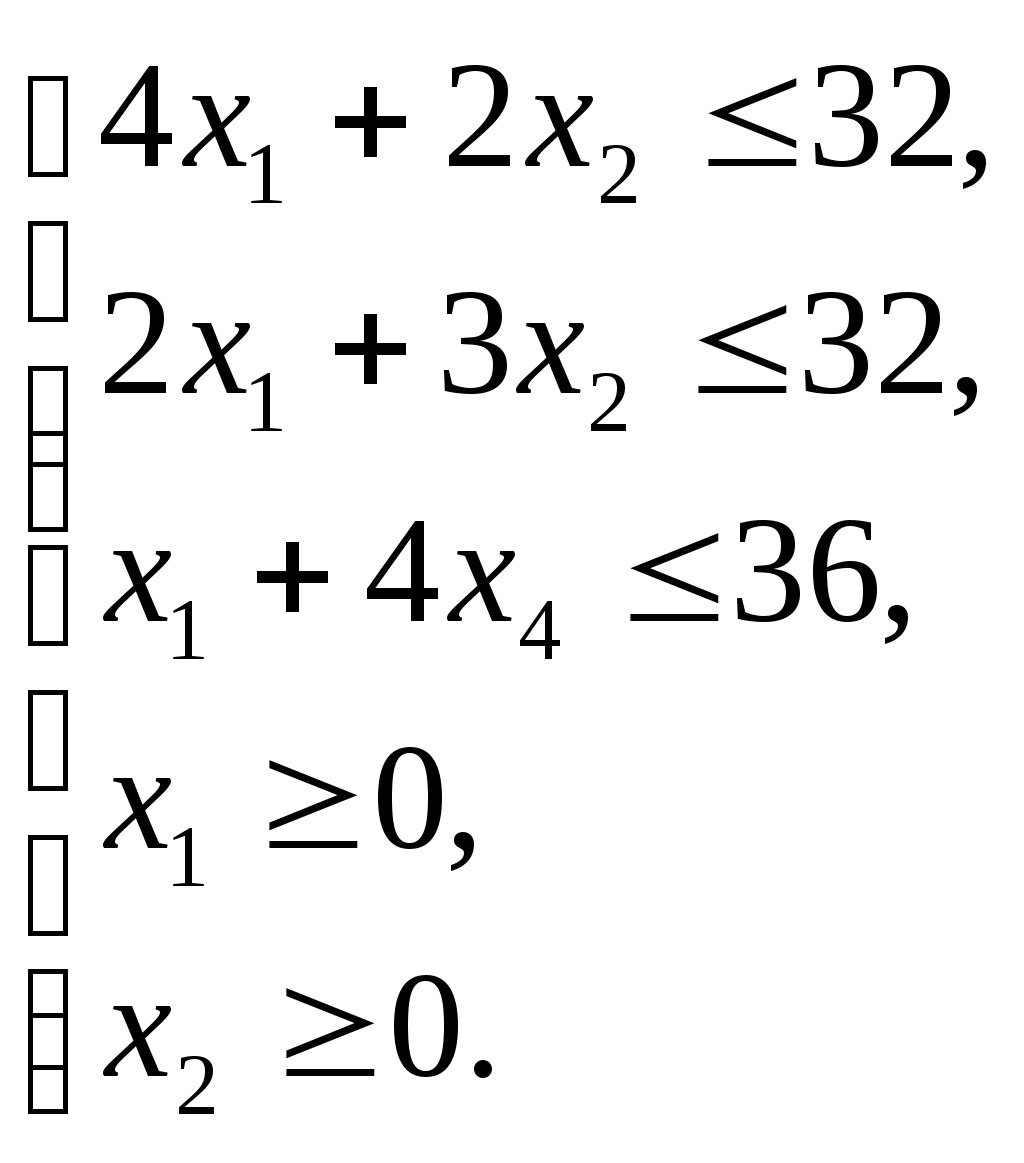



Построим область допустимых решений задачи.

(I) .

	0	8
	16	0

(II) .

	1	16
	10	0

(III) .

	0	16
	9	5

Построим полученные прямые, отметим стрелочками соответствующие полуплоскости допустимых значений переменных и их пересечение.

Х2

(I)

16

(II)

(III)

А

9

В

С

Х1

О

0

8

164

Областью допустимых решений задачи является четырехугольник ОABC.

Теперь среди этих точек нужно найти ту, в которой функция F будет иметь наибольшее значение.



вектор 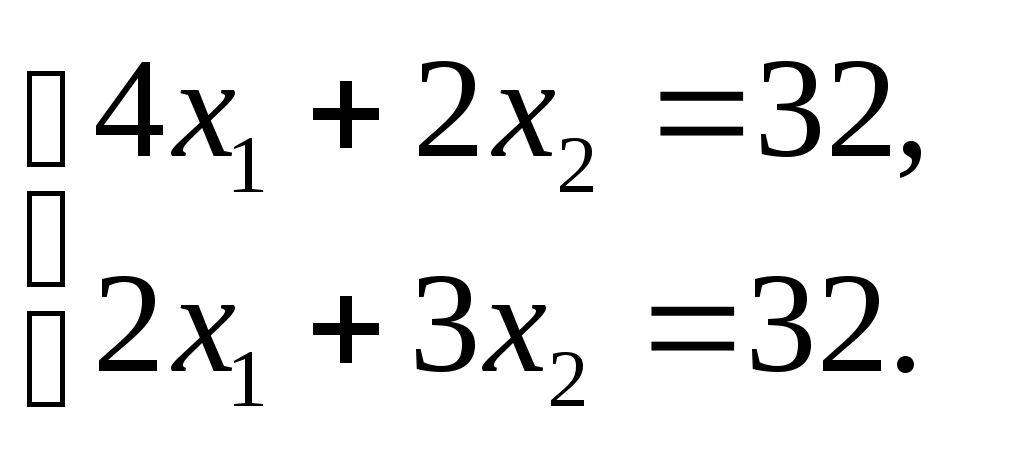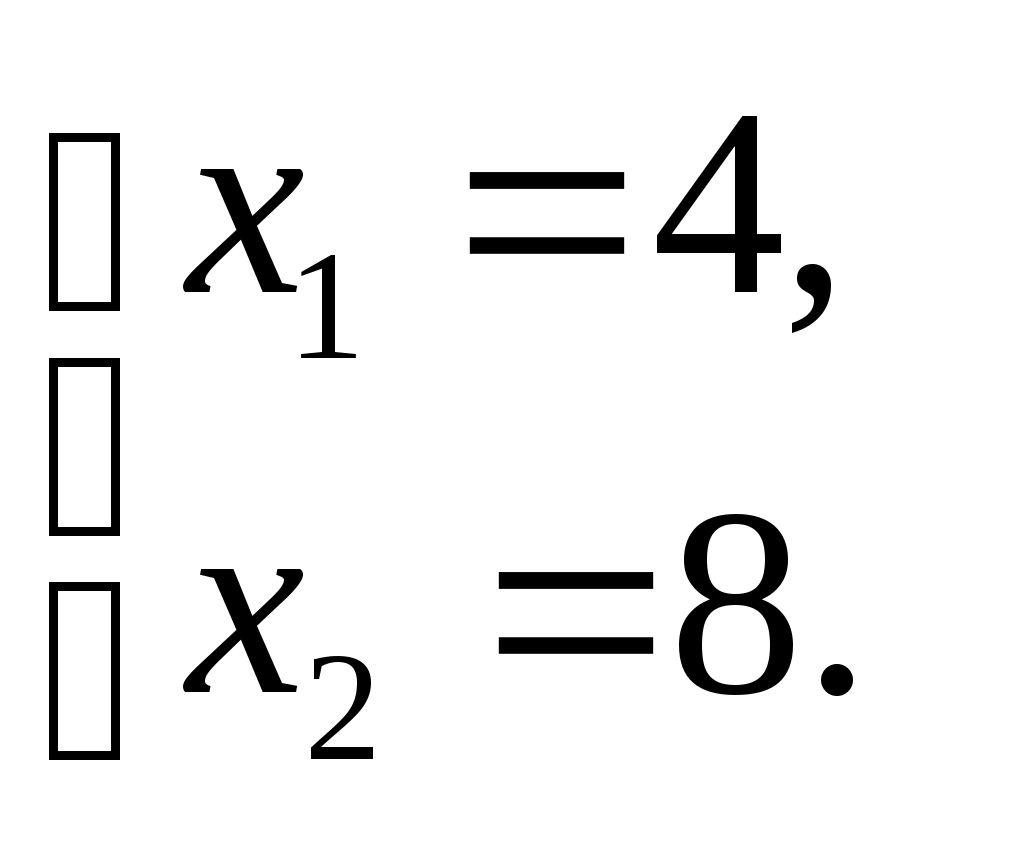, берем перпендикуляр этому вектору. Перемещаем перпендикуляр по направлению вектора до последней точки пересечения с четырехугольником ОABC. В нашем случае это точка В, где пересекаются прямые (I) и (II). Для нахождения ее координат решаем систему уравнений этих прямых:



(руб.)

Таким образом, оптимальный план задачи: выпуск 4 кирпичей М1 и 8 кирпичей М2; при этом прибыль будет максимальна и составит 84 руб.
Задача 2. Вероятность того, что в течении одной смены произойдет неполадка станка, равна 0,05. Найти вероятность того, что не произойдет ни одной неполадки в течении трех смен.
Решение

Пусть А - событие, не произошло ни одной неполадки за смену. Тогда Событие что не произошли неполадки в течении 3 смен

Р = Р (А) · Р (А) · Р (А) = 0,95 · 0,95 · 0,95 = 0,857.

Задача 3. Три цеха завода производят однотипные детали, которые поступают на сборку в общий контейнер. Известно, что первый цех производит изделий в 2 раза больше второго цеха и в 3 раза больше третьего цеха. В первом цехе брак составляет 6%, во втором - 10%, в третьем - 14%. Для контроля из контейнера берется одно изделие. Какова вероятность того, что изделие окажется стандартным (без брака).
Решение.

Обозначим через А событие, состоящее в том, что выбранное из контейнера для контроля изделие оказалось стандартным.

Пусть х – вероятность того, что изделие произведено 1-м цехом, тогда х/2 - вероятность того, что изделие произведено 2-м цехом, и х/3 - вероятность того, что изделие произведено 3-м цехом. Из равенства: получаем: .

Тогда имеем вероятности наступления каждой из указанных гипотез: ; ; .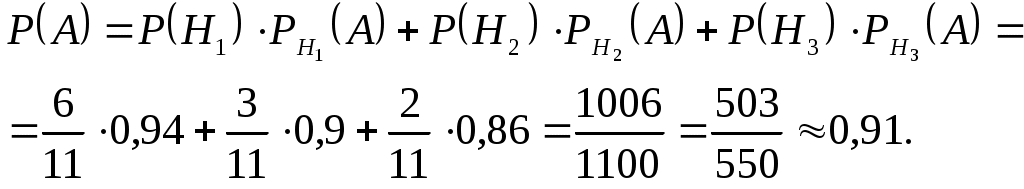

. Аналогично , .