Практическая работа по математике ММУ. Практическая работа 2. Решение Это дифференциальное уравнение второго порядка, допускающее понижение порядка
 Скачать 60.42 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Основы информационной культуры и информатика Группа Бз19М611 Студент Назаров Д.С МОСКВА 2019 Задание №1 Методом изоклин построить интегральные кривые уравнения:  Решение: Построим поле направлений для данного дифференциального уравнения. Изоклины, соответствующие направлениям поля с угловым коэффициентом равным  :  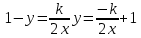Изоклинами являются кривые:  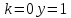 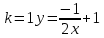     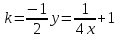 На каждую из изоклин наносим риски, угловой коэффициент которых равен . Эти риски являются касательными к интегральным кривым.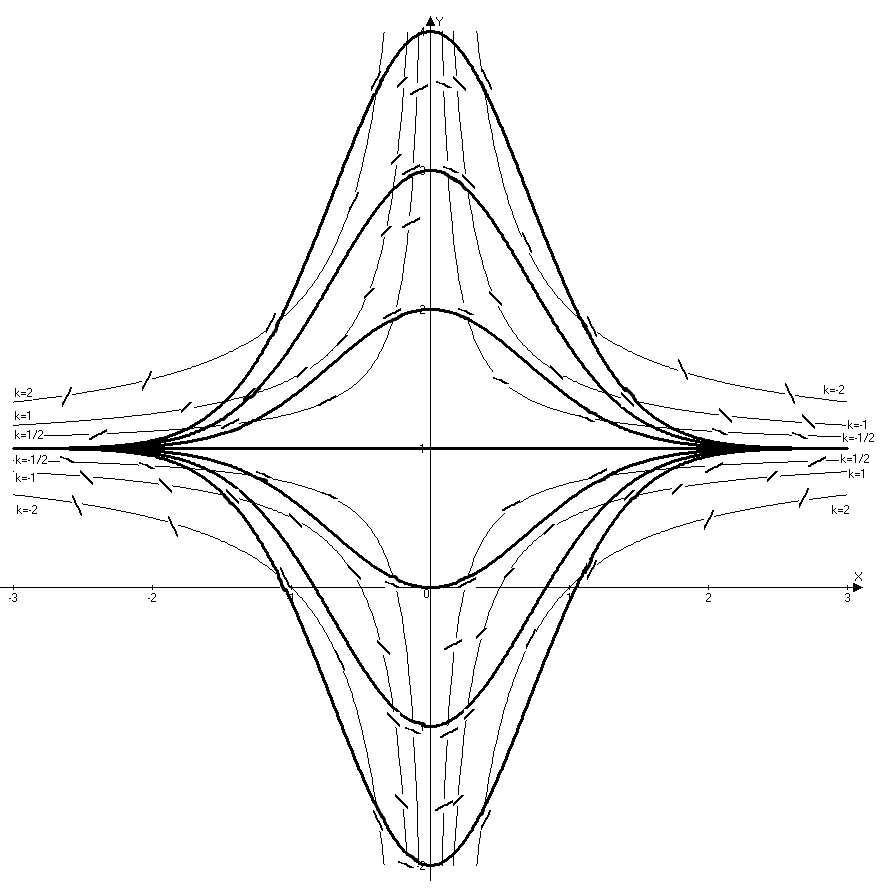 Решим данное уравнение аналитически: 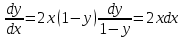 Проинтегрируем обе части уравнения: 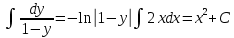   Задание №2 Решить уравнение, допускающее понижение порядка: 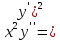 Решение: Это дифференциальное уравнение второго порядка, допускающее понижение порядка. Так как в уравнение явно не входит функция  , то выполним замену: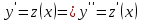 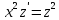  Интегрируем обе части уравнения.  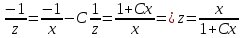  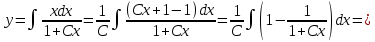  Задание №3 Решить систему уравнений: 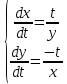 Решение: Выразим из каждого уравнения переменную  : 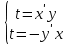 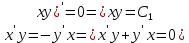 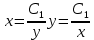 Интегрируем обе части: 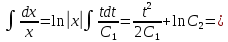 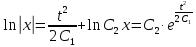 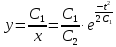 Получили решение системы дифференциальных уравнений:  Задание №4 Вероятность появления события в каждом испытании равна 0,7. Сколько необходимо провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10. Решение: Наивероятнейшее число появления события в серии независимых повторных испытаний можно найти из неравенства: По условию:   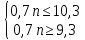 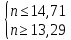 Так как количество испытаний целое число, то  |