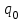Статистик. Решение Границы доверительного интервала определяются на основе точечной оценки и предельной погрешности выборки для средней
 Скачать 87.67 Kb. Скачать 87.67 Kb.
|
|
Задача 1 Поставлена задача проверки соблюдения графика движения автобусов. С этой целью проведено выборочное обследование работы 240 автобусов, что составляет 12% от их общего числа. Установлено, что время стоянки автобуса между рейсами в среднем составляет 23 минуты, при среднем квалратическом отклонении 7 мин. С какой вероятностью среднее время стоянки автобуса между рейсами не превысит 24 мин и не будет ниже 22 мин. Решение: Границы доверительного интервала определяются на основе точечной оценки и предельной погрешности выборки 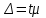 : :для средней  ; ;где — стандартная (средняя) погрешность выборки; t — квантиль распределения вероятностей (доверительное число). Предельная погрешность выборки 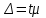 — это максимально возможная погрешность для взятой вероятности F(x). Доверительное число t показывает, как соотносятся предельная та стандартная погрешности. Для безповторной выборки предельная ошибка средней: — это максимально возможная погрешность для взятой вероятности F(x). Доверительное число t показывает, как соотносятся предельная та стандартная погрешности. Для безповторной выборки предельная ошибка средней: . .Объем выборочной совокупности n = 240, поскольку известно, что это составляет 12% всего объема генеральной совокупности, то можно вычислить объем генеральной совокупности  автобусов. автобусов.Среднее значение признака по выборочной совокупности (среднее время стоянки автобуса между рейсами):  23 минуты; среднее квадратическое отклонение: = 7 минут, следовательно, дисперсия равна 2 = 49 . 23 минуты; среднее квадратическое отклонение: = 7 минут, следовательно, дисперсия равна 2 = 49 . Таким образом, если осуществляется бесповторный отбор из генеральной совокупности, то предельная ошибка средней 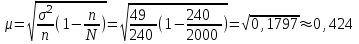 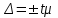 Пределы изменения среднего:  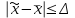 . .Нужно найти вероятность того,что среднее время стоянки автобуса между рейсами не превысит 24 мин и не будет ниже 22 мин., т.е.   или 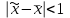  . .Получаем:  23, 23, 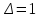  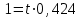  Здесь t такое значение функции Лапласа, что Ф(t)=γ, γ – доверительная вероятность. Функция Лапласа протабулирована и её значение можно найти в таблицах:  По таблицам находим, что Ф(2,36) = 0,9817. Ответ: С вероятностью 0,9817 среднее время стоянки автобуса между рейсами не превысит 24 мин и не будет ниже 22 мин. Задача 2. Предполагается изучить качество выпускаемой фабрикой обуви. Для этого требуется рассчитать, сколько пар обуви из выпускаемых в месяц 4800 пар необходимо исследовать на износоустойчивость. Подобное исследование, выполненной годом раньше, установило, что среднее квадратическое отклонение срока носки равно 60 дням. Предполагается, что в новом обследовании предельная ошибка среднего срока носки не должна превышать 4 дней, а выводы должны быть сделаны с вероятностью 0, 954. Решение: Одной из наиболее важных и ответственных задач при организации и проведении выборочного наблюдения является установление необходимой численности выборочной совокупности, т.е. такой ее численности, которая обеспечивала бы получение данных, достаточно правильно отражающих изучаемые свойства генеральной совокупности. При этом должно быть учтено: 1) с какой степенью точности следует получить предельную ошибку выборки; 2) какова должна быть вероятность того, что будет обеспечена обусловленная точность результатов выборочного наблюдения; 3) степень колеблемости изучаемых свойств в исследуемой генеральной совокупности. Это значит, что необходимая численность выборки (n) устанавливается в зависимости от размеров предельной ошибки выборки (), от величины коэффициента доверия (t) и от размеров величины дисперсии (  ). ).Данная задача относится задачам на нахождение необходимой численности единиц выборочной совокупности. Эта численность определяется из соответствующих соотношений, используемых при расчете предельных ошибок выборки. В частности, для безповторного отбора 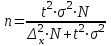 . .В нашей задаче  . .Для вероятности 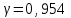 значение t = 2: значение t = 2:  Подставляем: 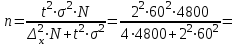 2057. 2057.Ответ: 2057 пар обуви из выпускаемых в месяц 4800 пар необходимо исследовать на износоустойчивость. Тогда предельная ошибка среднего срока носки не превысит 4 дней, а выводы будут сделаны с вероятностью 0,954. Таким образом, выборка численностью 2057 пар обеспечивает заданную точность при бесповторном отборе. Задача № 3 Имеются данные о производстве молока в сельскохозяйственных предприятиях области.
Определить: 1. Общие индексы продуктивности коров, их количества и общего надоя молока. Проверьте их взаимосвязь. 2. Абсолютное изменение общего надоя молока – всего и и т.ч. за счет изменения размера стада и продуктивности коров. Решение: Обозначим р0, р1 – продуктивность (среднегодовой надой) в базисном и отчетном годах, 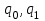 – численность стада (количество коров – численность стада (количество коров  ), тогда общий (валовый) надой ), тогда общий (валовый) надой  - базисный, - базисный,  - отчетный. - отчетный. Составим таблицу, в которую будем заносить данные и рассчитанные величины:
1. Общий индекс продуктивности коров: 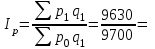 0,99 0,99Вывод: за счет изменения продуктивности надои уменьшились на 1% (100%– 99%). Общий индекс количества коров:  0,96 0,96Вывод: за счет изменения численности поголовья надои уменьшились на 4% (100%–96%). Общий индекс общего надоя молока: 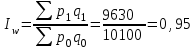 Вывод: надои уменьшились на 5% и составили 95% от базисного уровня. Взаимосвязь индексов: 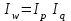 0,95 = 0,99 ∙ 0,96 = 0,95 - верно. 0,95 = 0,99 ∙ 0,96 = 0,95 - верно.2. Абсолютное изменение общего надоя молока – всего и и т.ч. за счет изменения размера стада и продуктивности коров. Построим систему в абсолютной форме: 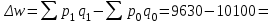 -470 тыс.кг -470 тыс.кг -70 тыс.кг -70 тыс.кг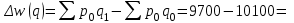 -400 тыс.кг -400 тыс.кгВзаимосвязь: 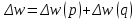 -470 = -70+ (-400) = -470 – верно. -470 = -70+ (-400) = -470 – верно.Вывод: в отчетном периоде по сравнению с базисным надои уменьшились на 470 тыс. кг, в том числе – на 70 тыс.кг за счет изменения продуктивности и на 400 тыс.кг за счет изменения размера стада. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||