длинный 4. Решение игры размера 2x2 Рассмотрим игру с наиболее простой платежной матрицей размера 2x2

• Название: Решение игры размера 2x2 Рассмотрим игру с наиболее простой платежной матрицей размера 2x2
• Дата: 29.11.2022
• Размер: 149.56 Kb.
• Имя файла: длинный 4.docx
• Тип: Решение; #819599

Аналитическое решение игры размера 2x2

Рассмотрим игру с наиболее простой платежной матрицей размера 2x2



Если матрица (1.15.1) имеет седловые точки, то игра имеет решение в чистых стратегиях. Нахождение этого решения по сути сводится к нахождению седловых точек (см. Алгоритм, § 1.6), процедура которого для матриц размера 2x2 весьма простая.

Можно сформулировать следующий критерий седловой точки матрицы игры 2x2, позволяющий вести поиск седловых точек на основе принципа доминирования.

Теорема 1.15.1. Пусть /,Лг е {1,2}, i Ф к,— номера строк, а j,l е {1,2}, j *1, — номера столбцов матрицы А размера 2x2 . Для того чтобы элемент я.. был седловой точкой матрицы А необходимо и достаточно выполнение хотя бы одного из следующих двух условий:

• 
  1. Можно удалить к -ю строку как доминируемую i -й строкой, а затем в оставшейся i - й строке можно удалить I -й столбец как доминируемый j -м столбцом;
  
• 
  2. Можно удалить 1-й столбец как доминируемый j -м столбцом, а затем в оставшемся j -м столбце удалить к -ю строку как доминируемую i -й строкой.
  

Другими словами, отсутствие у матрицы А размера 2x2 седловой точки эквивалентно отсутствию доминируемых (в частности дублируемых) строк и столбцов.

Доказательство. Необходимость. Пусть а₍. седловая точка. Тогда элемент

я,У является наименьшим в i -й строке и наибольшим ву'-м столбце:



При сравнении элементов я_/7 и а_ш, могут представиться два возможных случая:



или



Рассмотрим случай (1.15.4). Неравенства (1.15.3) и (1.15.4) означают, что /-я строка доминирует к-ю строку и потому к-ю строку можно удалить. Неравенство (1.15.2) означает, что в оставшейся /-й строке /-й столбец доминирустся j-м столбцом, а потому /-й столбец можно удалить. Таким образом, выполняется условие 1.

Рассмотрим случай (1.15.5). Из неравенств (1.15.3), (1.15.2) и (1.15.5) следует неравенство а^> ащ, которое вместе с неравенством (1.15.2) означает, что /-й столбец доминирустся j-м столбцом, и потому /-Й столбец можно удалить. Неравенство (1.15.3) означает, что в оставшемся j-м столбце /-я строка доминирует к-ю строку и, следовательно, к-ю строку можно удалить. Итак, выполняется условие 2.

Наконец, отмстим, что если выполняются неравенства (1.15.4) и (1.15.5), т.е., если



то, как следует из доказанного, выполняются условия 1 и 2. Однако, совместное выполнение условий 1 и 2 еще нс влечет за собой равенство (1.15.6).

Итак, необходимость доказана.

Достаточное 1Ь. Пусть выполняется условие 1. Тогда /-я строка доминирует к-ю строку, откуда, в частности, следует, что выполняется неравенство (1.15.3). Так как в /-й строке l-й столбец доминирустся /-м столбцом, то выполняется неравенство (1.15.2). Неравенства (1.15.2) и (1.15.3) означают, что я,у— седловая точка матрицы игры.

Пусть выполняется условие 2. Из того, что l-й столбец доминирустся j-м столбцом, следует неравенство (1.15.2), а из того, что в j-м столбце /-я строка доминирует к-ю строку, следует неравенство (1.15.3). Поэтому я,у— седловая точка игры ?

Пример 1.15.1. Рассмотрим игру с платежной матрицей



В матрице (1.15.7) 2-й столбец строго доминирует 1-й. Поэтому 1-й столбец нужно удалить. В результате останется 2-й столбец, в котором 1-я строка (3) строго доминирует 2-ю (2). Поэтому нужно удалить 2-ю строку. Останется матрица, единственным элементом которой является 3. Этот элемент и является седловой точкой исходной матрицы ?

Следующая теорема представляет достаточное условие существования седловых точек у платежных матриц размера 2x2.

Теорема 1.15.2. Для того чтобы у матрицы А размера 2x2 существовала седловая точка достаточно, чтобы сумма элементов главной диагонали матрицы А равнялась сумме элементов её побочной диагонали:

I

Доказательство. Из равенства (1.15.7) получаем:



Возможны лишь два случая:

или 

В случае (1.15.10) из (1.15.9) получаем неравенство а_2] <а₂₂, которое вместе с неравенством (1.15.10) означает, что 2-й столбец матрицы А доминируется её 1-м столбцом. Тогда на основании утверждения 3 следствия 1.13.1 существует оптимальная смешанная стратегия игрока В, в которую чистая стратегия В₂ входит с нулевой вероятностью. Другими словами: в данном случае стратегия В_] является оптимальной. Следовательно, по определению чистой оптимальной стратегии (см. § 1.6), у матрицы А существует седловая точка (стоящая в 1-й строке)

Если же имеет место случай (1.15.11), то из неравенства (1.15.9) вытекает неравенство а_2]>а₂₂, которое вместе с неравенством (1.15.11) означает строгое доминирование 1-го столбца матрицы/! её 2-м столбцом. Отсюда с помощью того же утверждения 3 следствия 1.13.1 заключаем, что стратегия В, оптимальна и, потому, по определению чистой оптимальной стратегии (см. § 1.6), у матрицы А существует седловая точка (стоящая во 2-м столбце) ?

Замечание 1.15.1. Условие (1.15.8), являясь по теореме 1.15.2 достаточным для существования у матрицы А размером 2x2 седловой точки, не является необходимым.

Действительно, в игре с матрицей (1.15.7) вышрыш а_п =3 является седловой точкой, но а, ( + а₂₂ = 4 + 2 = 6 Ф 8 = 3 + 5 = а_п + а_2] я

Перейдем к рассмотрению случая, когда матрица [2x2] — игры не имеет седловой точки. В этом случае решения в чистых стратегиях нет и надо переходить к смешанным стратегиям.

Теорема 1.15.3. Если матрица А размером 2x2 не имеет седловой точки, то каждый из игроков А и В обладает единственной оптимальной смешанной стратегией соответственно Р" = (р°,р“_) и Q° =(q",q₂), где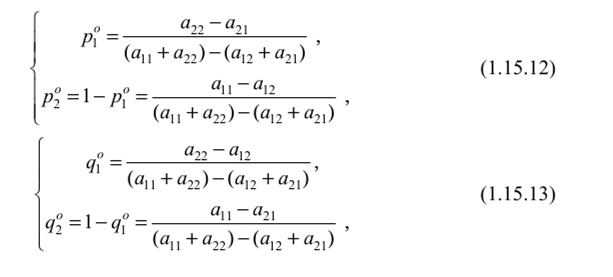



а цена игры V определяется формулой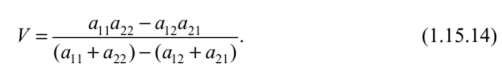



Доказательство. Так как матрица А не имеет седловой точки, то решения игры в чистых стратегиях не существует и сто надо искать в смешанных стратегиях. В этом случае но теореме 1.15.2 выполняется условие



т.с. знаменатель формул (1.15.12), (1.15.13), (1.15.14) отличен от нуля и, следовательно, эти формулы имеют смысл.

Пусть Р^а = {р",р") и Q° = (q° ,q₂)— оптимальные смешанные стратегии соответственно игроков А и В и V — цена шры (которые по основной теореме матричных шр фон Неймана всегда существуют). Тогда, по определению оптимальных стратегий (см. § 1.10), Н(Р°,Q°) = V.

Так как матрица/! нс имеет седловых точек, то стратегии В_] и В, активны в смешанной оптимальной стратегии Q° = (q“,q₂)- Действительно, если бы одна из них, например, стратегия В-,, была бы пассивной, то ц°₂ = 0 и тогда стратегия Q°

была бы чистой стратегией B_t. А так как стратегия Q = 5, оптимальна, то существовала бы седловая точка (находившаяся в 1-м столбце). Полученное противоречие доказывает активность стратегий /i, и В-, в оптимальной стратегии

Q°=(qlq°2)-

Тогда, но утверждению 2 теоремы 1.12.1 об активных стратегиях Н(Р°,В,)= V,j = 1,2. Записывая левые части этих равенств по формуле (1.8.7) и

присоединяя к ним нормировочное условие р" + р°_г = 1, получим систему трех линейных алгебраических уравнений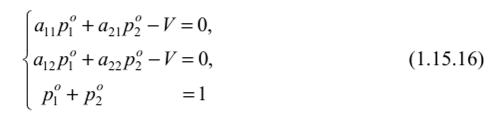 

с тремя неизвестными p°,p°₂,V. Определитель этой системы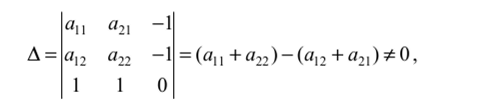



в силу (1.15.15). Поэтому система (1.15.16) имеет единственное решение, которое можно найти по формулам Крамера^[1]. Для этого вычислим определители



Габриэль Крамер (31.07.1704 - 04.01.1752)



Тогда по формулам Крамера: р" = А^,, jA, Рг = А^„/А. V = A_v/A,

получаем требуемые формулы (1.15.12) и (1.15.14).

Для доказательства формул (1.15.13) применяются аналогичные рассуждения, а именно, отсутствие седловых точек у матрицы А влечет активность стратегий А, и Л₂, откуда, по утерждению 1 теоремы 1.12.1.6 об активных стратегиях, получаем систему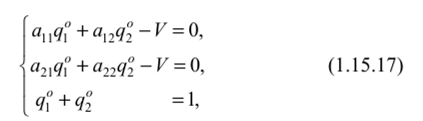 

определитель которой 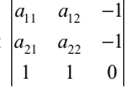 , как нетрудно убедиться, равен определителю А, а



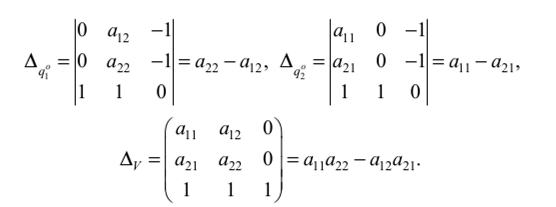матической экономикой. Крамера заслужено считают основоположником линейной алгебры. Методы Крамера сразу же получили дальнейшее развитие в трудах Безу, Вандермонда и Кэли, которые и завершили создание основ линейной алгебры. В 1751 году Крамер получает серьёзную травму после дорожного инцидента с каретой. Доктора рекомендуют ему отдохнуть на французском курорте Баньоль-сюр-Сез, но там его состояние ухудшается, и 4 января 1752 года Крамер умирает ([32], [119]-[122]).

По формулам Крамера q" = А^„ JA, q° = Д^„ JA, К = Д,./Д, получаем формулы (1.15.13) и (1.15.14).

В заключение доказательства отмстим, что цена шры V, найденная из системы (1.15.16) и из системы (1.15.17), естественно, совпадают ?

Замечание 1.15.2. В формулировке теоремы 1.15.3 условие отсутствия у матрицы седловой точки нельзя заменить более слабым условием (1.15.15).

Действительно, в игре с матрицей (1.15.7) выполняется условие (1.15.15): а_п+а„=4 + 2 = 6^8 = 3 + 5 = ар-1-а,,. Но выигрыш a_v = 3является седловой точкой и потому оптимальными стратегиями для ифоков А и В являются соответственно чистые стратегии А, и В₂. Таким образом, утверждение теоремы

1.15.3 не выполняется ?

Квадратная матрица А размера 2x2 называется симметрической, если ее элементы, симметричные относительно главной диагонали, равны, т.е. а_и = а₂₁.

Следствие 1.15.1. Если матрица игры А размером 2x2 симметрическая, и не имеет седловой точки, то чистые стратегии А_], Д и А^,В, входят в соответствующие оптимальные смешанные стратегии Р° = (р°,р₂) к Q = (qq") соответственно с равными вероятностями: р" = q", р₂ = q₂ .

Замечание 1.15.3. Симметричность матрицы А никак не связана с существованием у этой матрицы седловых точек.

В самом деле, матрица (1.15.7) имеет седловую точку, но не является сим- „ р, Г4 ЗЛ

метрической. С другой стороны, матрица ^ является симметрической, но не имеет седловых точек.

Следствие 1.15.2. Если у матрицы А размера 2x2 нет седловых точек и элементы главной диагонали равны между собой: а_]: = а₂₂, то у игроков А и В

существует по единственной оптимальной стратегии Р" =(р" ,р₂) и Q° = (q‘,q₂) соответственно, в которых р" =q₂, р₂ = q{’ ?

Квадратная матрица А размера 2x2 называется двояко симметрической, если ес элементы, симметричные относительно главной диагонали, равны между собой и элементы, симметричные относительно побочной диагонали также равны между собой, т.е. a_v =я->, и а_и =а„.

Следствие 1.15.3. Если матрица игры А размера 2x2 двояко симметрическая и не имеет седловой точки, то каждая из чистых стратегий A_hA₂, В_х, В-,

входит в соответствующую оптимальную стратегию Р°=(р",р") или

Q° = (q°,q₂) с вероятностью, равной 1/2: р° = р₂ = q" = q°₂ = 1/2, и цена игры V = (1/2 )(22 + а_2|).

Замечание 1.15.4. Двояко симметрическая квадратная матрица 2-то порядка нс имеет седловых точек, за исключением случая, когда все её элементы равны, и в этом случае каждый элемент является седловой точкой.

Пример 1.15.2. Рассмотрим игру с платежной матрицей

Л 4	В1	в2	Вз	В4	В5
А	си = 5	С2 = ^	С13 = 3	С|4=4	С|5 = 5
а2	С21 = 3	С22 = ^	С23 =6	С24 = 2	С25 = ^
Аз	с3, =4	?*32 = 5	С33=6	С34 = 2	С35 = ^
а4	с4| = 3	с42 = 6	С43 = 1	с44 = 2	С45 = А
а5	С51 = 5	С51 =8	С53 = 3	С54 =4	С55 = ^

(1.15.18)

Требуется найти решение игры. Сначала выясним, существует ли решение в чистых стратегиях. Предварительно упростим матрицу (1.15.18) с помощью принципа доминирования. 1-я строка строго доминирует 4-ю строку и дублирует 5-ю. Поэтому 4-ю и 5-ю строки можем удалить. В результате получим матрицу

V; 4	в,	в.	Вз	в4	В5
А	с =5	С2=5	с,3 = 3	С|4=4	С|5 = 5
а2	С2, — 3	С 22 = 3	с23 = 6	С24 = ^	с25 =8
Аз	с3)=4	С32 = ^	С33=6	С34 = ^	С35 = 6

(1.15.19)

В матрице (1.15.19) доминируемых строк нет, но 4-й столбец доминирует 1- й, 2-й и 5-й столбцы. Поэтому 1-й, 2-й и 5-й столбцы мы вправе удалить. В результате получим матрицу (1.15.20), в которой 2-я и 3-я строки дублирующие. Удалив в матрице (1.15.20) 3-ю строку, получим окончательно матрицу (1.15.21).

V, 4	Вз	*4
4	с,3 =3	<44= 4
Л2	С23 = ^	с 24 = 2
Аз	с33=6	ГД II т

(1.15.20)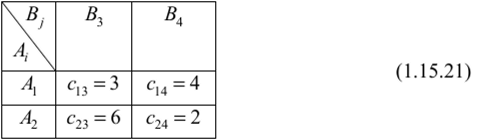



Очевидно, что матрица (1.15.21) седловых точек не имеет. Следовательно, игра с матрицей (1.15.21) и значит, исходная игра нс имеют решения в чистых стратегиях В игре с матрицей (1.15.21) существуют по теореме 1.15.3 оптимальные смешанные стратегии и цена шры, задаваемые формулами (1.15.12), (1.15.13), (1.15.14), в которых я, | =с_|3 =3, <я₁₂ = <г₁₄ = 4, a_2l=c_2i=6, a₂₂=c_2i=l: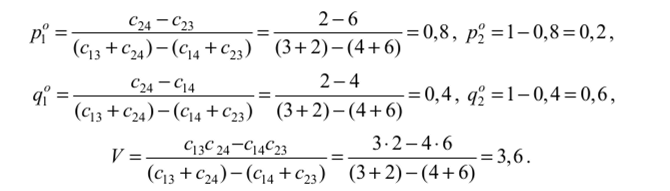



Таким образом, игра с матрицей (1.15.21) имеет цену V = 3,6, а Р° =(0,8; 0,2) и Q° = (0.4; 0,6) оптимальные стратегии соответственно игроков А и В. Тогда в исходной игре с платежной матрицей (1.15.18) ценной является V = 3,6 а оптимальными стратегиями игроков А и В являются соответственно

Р° =(0,8; 0,2; 0; 0; 0) и Q° =(0; 0; 0,4; 0,6; 0).

Сравним нижнюю и верхнюю цены игры с платежной матрицей (1.15.18) с ценой игры V = 3,6. Из матрицы (1.15.18) находим показатели эффективности и неэффективности стратегий соответственно игроков А и В: а, =3, а, = 2, а, = 2, ос₄ = 1, а₅ = 3 и р, = 5, р, = 8, Р, =6, Р₄ = 4, Р₅ = 8. Следовательно, нижняя цена игры в чистых стратегиях а = 3, а верхняя цена игры Р = 4. Свободный вышрыш р - а = 1. Наименьшим гарантированным выигрышем шро- ка А является нижняя цена игры а = 3, а наибольшим гарантированным проигрышем игрока В является верхняя цена игры Р = 4. В смешанных стратегиях в среднем игрок А выигрывает V = 3,6, а шрок В ирошрываст V = 3,6. Таким образом, в смешанных стратегиях игрок А выигрывает на V -а = 3,6-3 = 0,6 больше, а шрок В ирошрываст на Р —F = 4 —3,6 = 0,4 меньше. Отсюда видно, как при переходе к смешанным стратегиям распределяется но игрокам свободный выигрыш р-ос = 1 ?