Решение игры в смешанных стратегиях Цель лабораторной работы

• Название: Решение игры в смешанных стратегиях Цель лабораторной работы
• Дата: 01.12.2022
• Размер: 450.3 Kb.
• Имя файла: shablya_yuv_-_metod-ukaz-dlya_lab-rab-maket_pdf (1).docx
• Тип: Решение; #823872

ЛАБОРАТОРНАЯ РАБОТА

Решение игры в смешанных стратегиях

Цель лабораторной работы

Ознакомление с играми в нормальной форме на примере задачи решения матричных игр и её реализация в математических пакетах.

Матричная игра

Матричная игра – это антогонистическая игра, которая задаётся набором чистых стратегий {X₁, …, X_n} и {Y₁, …, Y_m} первого и второго игроков, а так-

же платёжной матрицей _a_ij

, определяющей выигрыш первого игрока

nm

(или проигрыш второго игрока) при выборе игроками чистых стратегий X_iи

Y_jсоответственно.

Антагонистическая игра – это некооперативная игра двух игроков, выиг- рыши которых противоположны.

Цель первого игрока – максимизация своего выигрыша.

Цель второго игрока – минимизация выигрыша противника.

Решение матричных игр в чистых стратегиях Принцип максимина

Предположим, что второй игрок заранее знает все ходы первого игрока. Тогда на каждую стратегию X_iон отвечает наилучшей контрстратегией Y_j(i),

для которой a_ij(i)  a_ij

для всех


j1,m.

Оптимальной чистой стратегией первого игрока является стратегия X_p

(максиминная стратегия), для которой выполняется:

 

max _ min a_ij  a_pq .

1in_1 jm _

Величину  называют нижней ценой игры в чистых стратегиях. Принцип минимакса

Рассмотрим аналогичную ситуацию для первого игрока.

Оптимальной чистой стратегией второго игрока является стратегия Y_q

(минимаксная стратегия), для которой выполняется:

min ^ max a

^  a

 .



1 jm1in

ij pq



Величину  называют верхней ценой игры в чистых стратегиях.

Нижняя цена игры не может быть больше верхней цены игры (   v ).

Цена игры в чистых стратегиях – значение выигрыша первого игрока при условии выбора игроками их оптимальных чистых стратегий.

Стратегия

X_p1

доминирует стратегию

X_p2 , если для всех


j1,m

спра-

ведливы неравенства

a_p1k a_p2k.

^ap₁ j^{ a}p₂ j

и существует такая стратегия

Y_k, что

Стратегия Y_q1

доминирует стратегию Y_q2 , если для всех


i1,n

справед-

ливы неравенства

a_kq1  a_kq2 .

^aiq₁ ^{ a}iq₂

и существует такая стратегия

X_k, что

Решение матричных игр в смешанных стратегиях

Если нижняя и верхняя цены игры не совпадают (   ), то решения мат-

ричной игры в чистых стратегиях не существует. В таких случаях ищут ре- шение игры в смешанных стратегиях.

Смешанная стратегия – это произвольное вероятностное распределение на множестве чистых стратегий:

^P ^p₁^{,, p}_n

n

• 
  смешанная стратегия первого игрока, _ p_i1 ;
  

i1 m

^Q^q1,,q_m

• 
  смешанная стратегия второго игрока,
  

_ q_j1 .

j1

Цена игры в смешанных стратегиях – это математическое ожидание выигрыша первого игрока при применении игроками смешанных стратегий P и Q:

nm

v _ a_ijp_iq_j.

i1 j1


n
Так как P– оптимальная смешанная стратегия первого игрока, то она должна давать выигрыш первого игрока не меньший, чем цена игры v, тогда:

_a_ijp_i v_ j1,m_.

i1

Разделим эти неравенства на цену игры vи обозначим x_i^pi, получаем:

v

n

_a_ijp_i1

i1

_ j1,m_,

v v
F n p n^pi ¹  min.

 i

i1



i1

Допустим, что цена игры v 0 , получаем задачу линейного программиро- вания:

F n p ¹  min,




 i

i1 ^v

_ n

^^aij^pi^1

_ j1,m_,

^i1



^x_i 0 _i1,n_.

Цена игры в смешанных стратегиях: v ¹ .

F

Оптимальная смешанная стратегия первого игрока:
p_i v x_ii1,n_.

Применяя аналогичные рассуждения для второго игрока, получаем сле- дующую задачу линейного программирования:

m

F _ q_jj1

 ¹  max,

v


m

^ ^aij^qj^1

_i1,n_,

^ j1



^y_j 0 _ j1,m_.

Оптимальная смешанная стратегия второго игрока: q_j v y<sub>j

</sub> j1,m_.

Игра с природой

Рассмотрим ситуацию неопределённости – ситуация, когда противник не имеет противоположных интересов, но выигрыш действующего игрока во многом зависит от неизвестного заранее состояния противника. В таких задачах выбор решения зависит от состояния объективной действительности, называемой «природой», а математические модели называются «Игры с природой».

Игра с природой – игра, в которой осознанно действует только один из игроков.

Природа – это обобщенное понятие противника, который не преследует собственных целей в данном конфликте (такая ситуация может быть названа конфликтом лишь условно).

Природа может принимать одно из своих возможных состояний и не име- ет целью получение выигрыша. Игра с природой представляется в виде пла- тёжной матрицы, элементы которой – это выигрыши игрока, которые не яв- ляются проигрышами природы. Для отбора стратегии применяют критерии оптимальности.

Критерий оптимизма: предназначен для выбора наибольшего элемента платёжной матрицы из её максимально возможных элементов:

K_O

 

max _ max a_{ij }.

1in_1 jm _

Данный критерий используется тогда, когда игрок оказывается в безвы- ходном положении и любой его шаг равновероятно может оказаться абсо- лютным выигрышем или полным провалом. При этом предполагается, что развитие ситуации будет благоприятным для игрока. Вследствие этого, опти- мальным выбором будет вариант с наибольшим значением выигрыша в пла- тёжной матрице.

Критерий пессимизма: предназначен для выбора наименьшего элемента платёжной матрицы из её минимально возможных элементов:

K_P

 

min _ min a_ij.

1in_1 jm _

Данный критерий используется тогда, когда игрок оказывается в безвы- ходном положении и любой его шаг равновероятно может оказаться абсо- лютным выигрышем или полным провалом. При этом предполагается, что возможна потеря контроля над ситуацией, поэтому необходимо исключить все потенциальные риски и выбрать вариант с минимальным выигрышем.

Критерий Вальда предназначен для выбора наибольшего элемента пла- тёжной матрицы из её минимально возможных элементов:

K_W

 

max _ min a_ij.

1in_1 jm _

Данный критерий обеспечивает максимизацию минимального выигрыша, который может быть получен при реализации каждого из вариантов страте- гий. Критерий ориентирует игрока на осторожную линию поведения, направ- ленную на получение дохода и минимизацию возможных рисков одновре- менно.

Критерий Сэвиджа предназначен для выбора наименьшего элемента матрицы рисков из её максимально возможных элементов:

K_S

 

min _ max r_ij.

1in_1 jm _

Необходимо провести оценку рисков в условиях, когда реальная ситуация неизвестна. Если бы игрок знал, что будет j-е состояние природы, то выбрал бы наилучшее решение, то есть то, которое принесёт наибольший выигрыш:

max a_ij.

1in

Матрица рисков характеризует риск выбора определённого варианта стра- тегии:

r_ij max a_ij a_ij.

1in

Пессимистично настроенный игрок предполагает, что состояние природы будет таким, что для любой его стратегии риск будет максимальным, поэтому он выбирает такую стратегию, для которой риск будет минимальным.

Критерий Гурвица: предназначен для выбора среднего элемента платёж- ной матрицы, отличающегося от крайних минимального и максимального состояний:


 
^K_H^{ max  max a}_ij^^{1 }^{ min a}_ij^.

1in_

1 jm

1 jm _

Данный критерий ориентирован на установление баланса между случаями крайнего пессимизма и крайнего оптимизма, позволяет избежать погранич- ных состояний при принятии решения и выбрать наиболее вероятный вариант стратегии, обеспечивающий наилучшую эффективность. Коэффициент опти-

^{мизма } ^{0  1} ^{выражает количественно меру оптимизма игрока при вы-}

боре стратегии и определяется им из субъективных соображений на основе статистических исследований или личного опыта.

Обобщённый критерий для выбора наиболее эффективного варианта стратегии применяются все критерии оптимальности одновременно: каждый из критериев позволяет отобрать только один вариант, оптимальным же будет являться та стратегия, на которую указывает большинство критериев опти- мальности.

Задание

1. 
   Выберите и согласуйте с преподавателем средство практической реали- зации решения матричных игр (допускается использовать любые математиче- ские пакеты и языки программирования).
   
2. 
   С помощью теста электронного курса «Домашнее задание №14. Инди- видуальное задание №3» сгенерируйте условия четырёх задач и сохраните их.
   

3. 
   Решите сгенерированные задачи с помощью выбранного средства прак- тической реализации.
   
4. 
   Проведите анализ полученных результатов.
   
5. 
   Составьте отчёт по проделанной работе, оформление отчёта должно со- ответствовать требованиям ОС ТУСУР 01.2013. Содержание отчёта:
   
   1. 
      титульный лист (пример оформления приведён в приложении А);
      
   2. 
      введение: цель лабораторной работы, краткая теоретическая справка, описание выбранного средства практической реализации;
      
   3. 
      задача: условие сгенерированной задачи;
      
   4. 
      практическая реализация: описание основных этапов выполнения практической реализации решения задачи с помощью выбранного средства, описание основных функций программы и так далее;
      
   5. 
      решение задачи: демонстрация полученного решения задачи с помо- щью выбранного средства практической реализации;
      
   6. 
      заключение: выводы по проделанной работе.
      
6. 
   Отправьте файл отчёта в формате PDF через соответствующее задание электронного курса «Лабораторная работа №6: Матричные игры».
   
7. 
   Отправьте файл архива с реализацией решения через соответствующее задание электронного курса «Лабораторная работа №6: Матричные игры (реализация)».
   
8. 
   Защитите отчёт.
   

Ход работы

С помощью теста электронного курса «Домашнее задание №14: Индиви- дуальное задание №3» генерируем условия четырёх задач (рис. 6.1–6.4).

Рис. 6.1. Условие сгенерированной задачи №1


Рис. 6.2. Условие сгенерированной задачи №2

Рис. 6.3. Условие сгенерированной задачи №3



Рис. 6.4. Условие сгенерированной задачи №4

Рассмотрим пример решения сгенерированных задач с помощью про- граммы Microsoft Excel.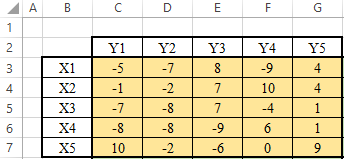

Записываем исходные данные задачи №1 (рис. 6.5).

Рис. 6.5. Исходные данные задачи №1 в Microsoft Excel

С помощью функций «МИН()» и «МАКС()» вычислим значение нижней цены игры  2 (рис. 6.6).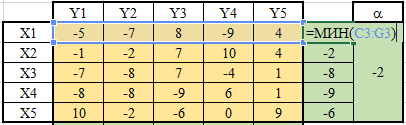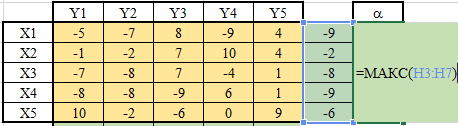





Рис. 6.6. Расчёт нижней цены игры

Аналогично определяем значение верхней цены игры  2 (рис. 6.7).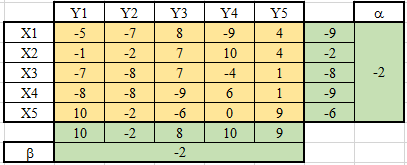




Рис. 6.7. Расчёт верхней цены игры

Так как нижняя и верхняя цены игры совпадают (   2 ), значит в дан- ной матричной игре существует решение в чистых стратегиях (рис. 6.8):

• 
  X₂ – оптимальная чистая стратегия первого игрока;
  
• 
  Y₂ – оптимальная чистая стратегия второго игрока;
  
• 
  v a_pq a₂₂  2 – цена игры в чистых стратегиях.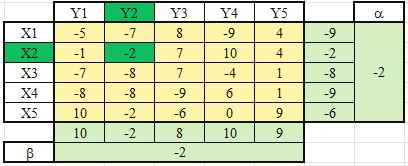
  

Рис. 6.8. Решение в чистых стратегиях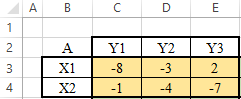

Записываем исходные данные задачи №2 (рис. 6.9).

Рис. 6.9. Исходные данные задачи №2 в Microsoft Excel

С помощью функций «МИН()» и «МАКС()» определяем значения нижней цены игры  7 и верхней цены игры  3 (рис. 6.10).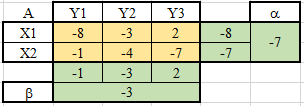




Рис. 6.10. Расчёт нижней и верхней цен игры

Так как нижняя и верхняя цены игры не совпадают (   ), значит в дан-

ной матричной игре нет решения в чистых стратегиях, поэтому необходимо найти решение в смешанных стратегиях. Для этого сначала необходимо пре- образовать платёжную матрицу, избавившись от отрицательных платежей (рис. 6.11).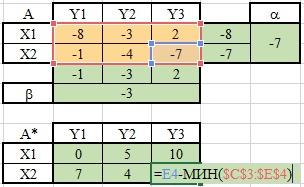


Рис. 6.11. Преобразование платёжной матрицы

По преобразованной платёжной матрице составляем задачу линейного программирования для первого игрока:

F1x₁ 1x₂ min,

^0x₁ ^{ 7x}₂ <sup>1,

</sup>5x 4x1,

^ 1 2



_10x₁ 1x₂ 1,

^_x₁, x₂  0.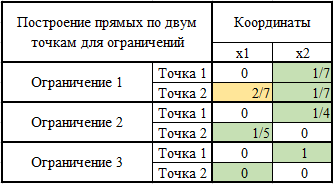

Чтобы построить область допустимых решений в соответствии с ограни- чениями, необходимо для каждого ограничения построить прямую по двум точкам (рис. 6.12).

Рис. 6.12. Координаты точек для построения прямых

Далее нужно построить прямые на графике (рис. 6.13).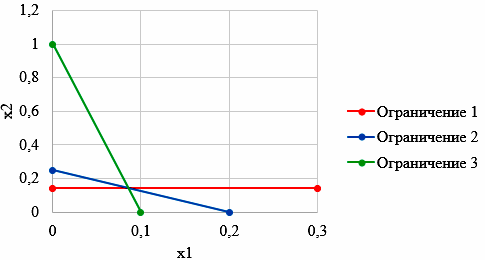


Рис. 6.13. Прямые, соответствующие ограничениям на ресурсы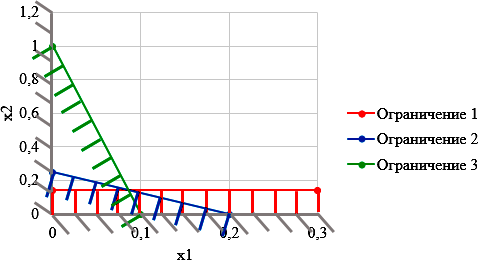

Затем для каждой прямой определяем полуплоскость, которая удовлетво- ряет ограничению, и делаем соответствующие отметки – заштриховываем полуплоскость, которая не удовлетворяет ограничению (рис. 6.14). При этом нужно не забыть об ограничении на неотрицательность переменных.

Рис. 6.14. Отметки о соответствии ограничениям
В результате получаем область допустимых решений (рис. 6.15).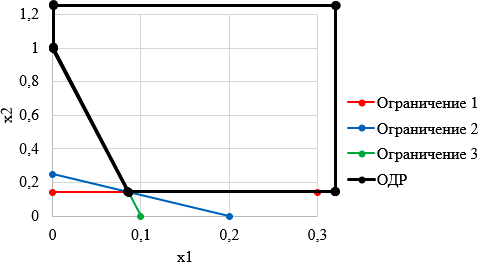


Рис. 6.15. Область допустимых решений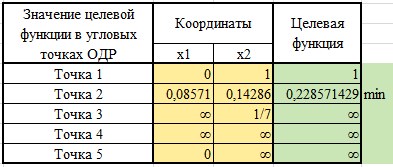

Запишем в виде таблицы координаты угловых точек области допустимых решений. Также вычислим значение целевой функции в каждой угловой точ- ке области допустимых решений (рис. 6.16).

Рис. 6.16. Координаты угловых точек и расчёт значений целевой функции
Получаем решение для задачи линейного программирования:

x₁  ³  0,08571,

35

x₂  ¹  0,14286,

7

F1x₁ 1x₂  ⁸ .

35

На основе полученного решения находим решение в смешанных стратеги- ях для исходной матричной игры (рис. 6.17):

v^*  ¹  ³⁵;

F 8

p₁  v^*  x₁  ³⁵  ³  ³;

8 35 8

p₂  v^*  x₂  ³⁵  ¹  ⁵;

8 7 8


8 8 8
^{v v*  min}^a_ij^{ 35 }^8 ^{ 35  64   29.}





Рис. 6.17. Решение в смешанных стратегиях (графический метод)
В рамках задачи №3 необходимо решить такую же задачу, но для двух иг- роков, используя симплекс-метод. Для этого нужно найти решение следую- щих двух задач линейного программирования:

• 
  для первого игрока:
  

F₁ 1x₁ 1x₂ min,

<sup>0x1  7x2 1,

</sup>5x 4x1,

^ 1 2

^ x₁ 1x₂ 1,

_10

^_x₁, x₂  0.

• 
  для второго игрока (двойственная задача):
  

F₂ 1y₁ 1y₂ 1y₃ max,



^{0 y1  5 y2 10 y3 1,}

_7 y₁  4 y₂ 1y₃ 1,



^y₁, y₂ , y₃  0.

Получим решение для данных задач с помощью надстройки «Поиск реше- ния». Подготавливаем исходные данные для первой задачи линейного про- граммирования (рис. 6.18).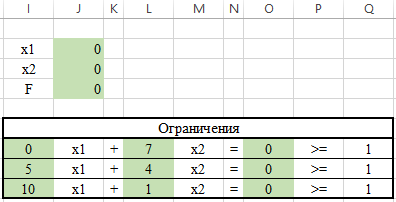




Рис. 6.18. Исходные данные для первой задачи линейного программирования
Подготавливаем исходные для второй задачи линейного программирова- ния (рис. 6.19).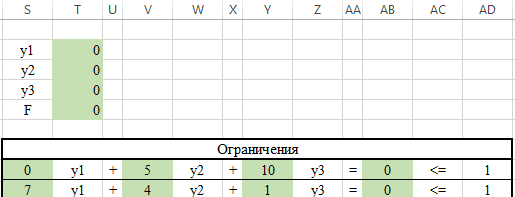




Рис. 6.19. Исходные данные для второй задачи линейного программирования
Далее открываем надстройку «Поиск решения» и вносим всю необходи- мую информацию о задаче линейного программирования (рис. 6.20).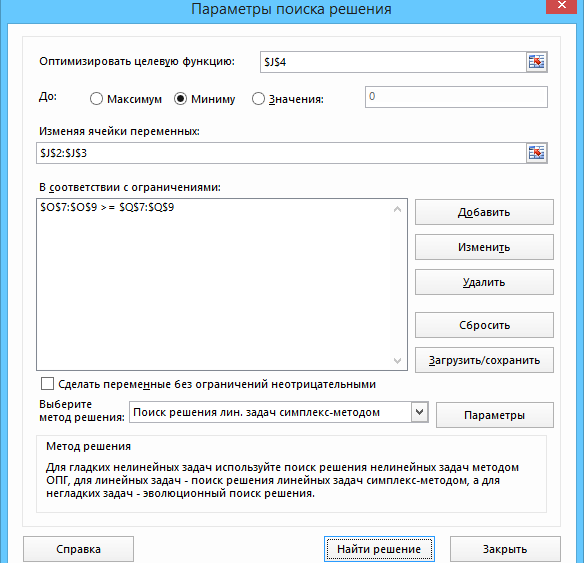

Рис. 6.20. Надстройка «Поиск решения»

для первой задачи линейного программирования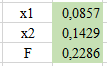

В результате получаем оптимальное решение, которое полностью совпа- дает с решением с помощью графического метода (рис. 6.21).

Рис. 6. 21. Решение для первой задачи линейного программирования

На основе полученного ответа находим решение в смешанных стратегиях для первого игрока (рис. 6.22).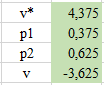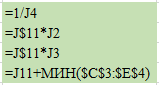


Рис. 6. 22. Решение в смешанных стратегиях для первого игрока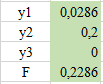

Аналогично находим решение для второй задачи линейного программиро- вания. В результате получаем оптимальное решение для двойственной задачи (рис. 6.23).

Рис. 6.23. Решение для второй задачи линейного программирования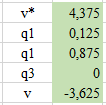

На основе полученного ответа находим решение в смешанных стратегиях для второго игрока (рис. 6.24).

Рис. 6.24. Решение в смешанных стратегиях для второго игрока

Записываем исходные данные задачи №4 (рис. 6.25).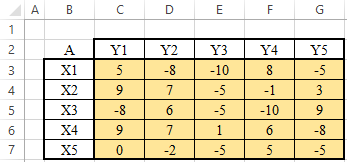




Рис. 6.25. Исходные данные задачи №4 в Microsoft Excel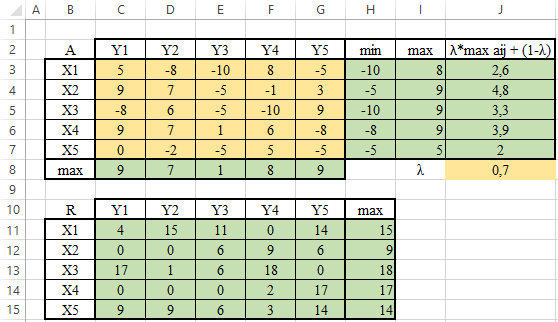

С помощью функций «МИН()» и «МАКС()» вычислим все вспомогатель- ные значения, которые необходимы для расчёта критериев оптимальности (рис. 6.26).

Рис. 6.26. Расчёт вспомогательных значений для критериев оптимальности

Далее с помощью функций «МИН()» и «МАКС()» вычислим значения критериев оптимальности (рис. 6.27). Также с помощью функции «ЕСЛИ()» делаем соответствующие отметки об оптимальности стратегий. В результате получаем, что по обобщённому критерию лидирует стратегия X₂, так как она является оптимальной по большинству критериев оптимальности – критерии оптимизма, Вальда, Сэвиджа и Гурвица (рис. 6.28).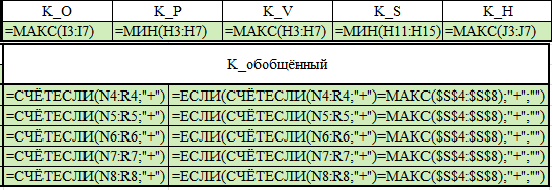




Рис. 6.27. Расчёт критериев оптимальности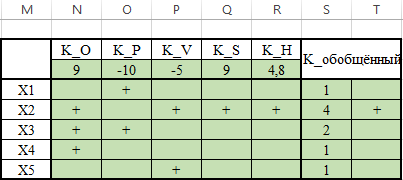


Рис. 6.28. Значения критериев оптимальности

Контрольные вопросы

1. 
   Что такое матричная игра?
   
2. 
   Что такое оптимальная чистая стратегия?
   
3. 
   Что такое цена игры в чистых стратегиях?
   
4. 
   Опишите процесс удаления доминируемых стратегий.
   
5. 
   Что такое оптимальная смешанная стратегия?
   
6. 
   Что такое цена игры в смешанных стратегиях?
   
7. 
   Что такое игра с природой? Чем она отличается от матричной игры?
   
8. 
   Опишите критерий оптимизма/пессимизма/Вальда/Сэвиджа/Гурвица.