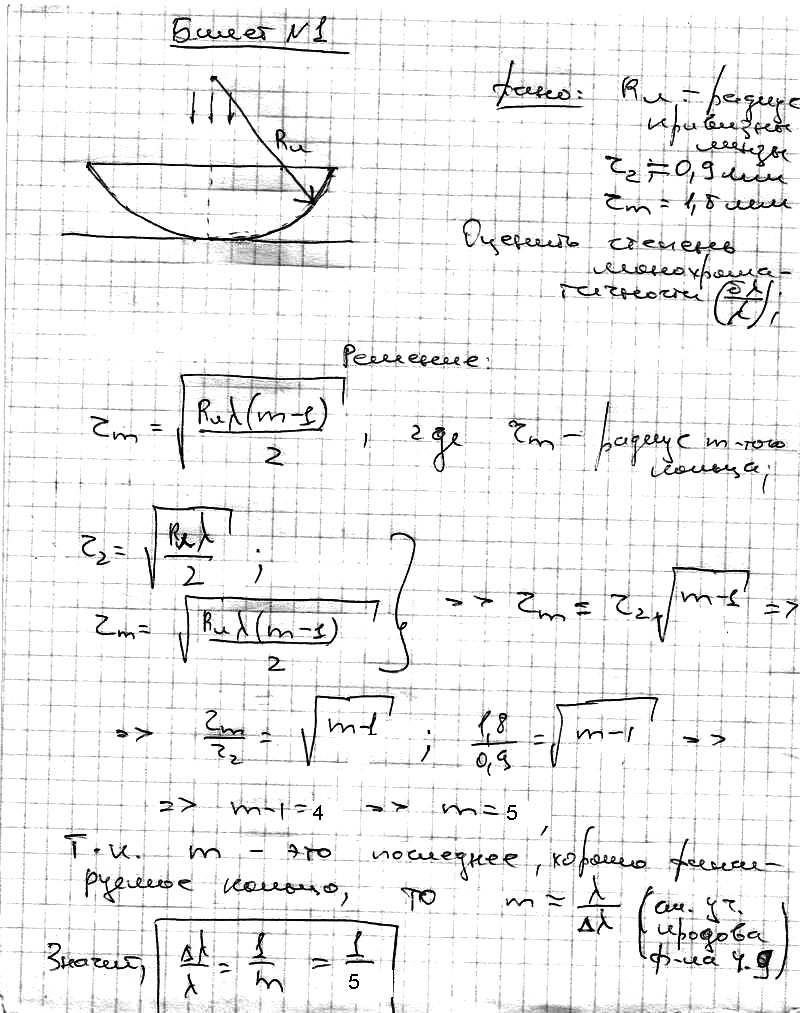
Решение Используем формулы 2а) и 4) для интерференционных минимумов в отраженном свете в точкахАиСс порядковыми номерами

• Название: Решение Используем формулы 2а) и 4) для интерференционных минимумов в отраженном свете в точкахАиСс порядковыми номерами
• Анкор: zadachi.doc
• Дата: 02.04.2017
• Размер: 23.73 Mb.
• Имя файла: zadachi.doc
• Тип: Задача; #4428

БИЛЕТ №1.

3.При прохождении в некотором веществе пути l интенсивность света I уменьшается в 2 раза. Во сколько раз уменьшается I при прохождении пути 3l?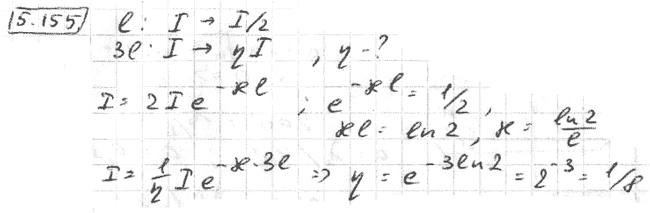



4.Сила тока в проводнике сопротивлением R=20 Ом нарастает в течение времени ∆t=2с по линейному закону от I₁=0А до I_max=6А. Определить количество теплоты Q₁, выделившееся в этом проводнике за первую секунду и Q₂ − за вторую, а также найти отношение этих количеств теплот Q₂/Q₁.



БИЛЕТ №2.

3.Свет с длиной волны λ=0,55 мкм падает нормально на поверхность стеклянного (n=1,5) клина. В отраженном свете наблюдают систему интерференционных полос, причем, расстояние между соседними темными полосами ∆x=0,21 мм. Определить угол между гранями клина. (1 рад=3,4́ · 10³)

Задача 4

Н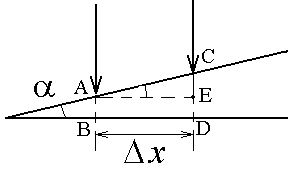


Рис.5
а стеклянный клин с углом и показателем преломления n = 1,5 нормально падает монохроматический свет с длиной волны  = 0,6 мкм (см. рис.5). Определить расстояние между двумя соседними интерференционными минимумами в отраженном свете х.

Решение:

Используем формулы (2.2а) и (2.4) для интерференционных ми­ни­мумов в отраженном свете в точках А и С с порядковыми номерами mи (m + 1):

, (3.4)

. (3.5)

Из прямоугольного треугольника АСЕ на рис.5 можно найти длину катета :

(3.6)

Вычитая (3.4) из (3.5), найдем длину катета :

(3.7)

Подставляя (3.7) в (3.6), найдем :

м

Ответ: 0,687 мм


4.Пространство между обкладками плоского конденсатора заполнено последовательно двумя диэлектрическими слоями 1 и 2 толщины d₁ и d₂ и проницаемости ε₁ и ε₂. Площадь каждой обкладки равна S. Найти плотность σ* связанных зарядов на границе раздела слоев, если напряжение на конденсаторе равно U и электрическое поле направлено от слоя 1 к слою 2.



БИЛЕТ №3.

3.В некоторой точке А внутри однородного диэлектрика с проницаемостью ε =2,5 плотность стороннего заряда ρ=50 мкл/м³. Найти в этой точке плотность связанных зарядов.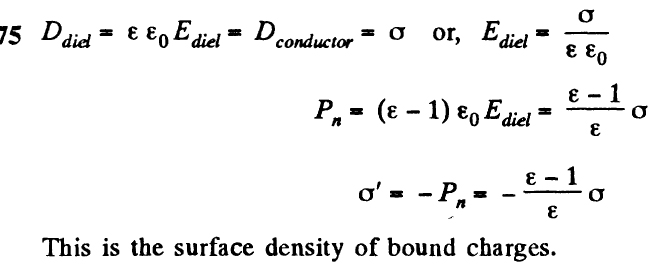



Величина ρ’=- ρ(e-1)/e=-30 мкКл/м^3
4.Металлический шар радиусом R=3см несет заряд Q=20 нКл. Шар окружен слоем парафина(ε =2) толщиной d =2 см. Определить энергию W электрического поля, заключенную в слое диэлектрика.



БИЛЕТ №4.

3.Длинный цилиндр радиусом R=4 см из диэлектрика (ε =4) заряжен по объему с постоянной объемной плотностью ρ =2 · 10^-8 Кл/м³. Найдите энергию поля, локализованного внутри цилиндра, приходящуюся на единицу его длины.


4.Какой разностью потенциалов надо ускорить протон, чтобы его энергия оказалась достаточной для достижения поверхности ядра железа? Заряд ядра железа в 26 раз больше заряда протона (≈|e|), а его радиус равен R=4,0 · 10^-15 м. Считайте ядро однородно заряженным шаром.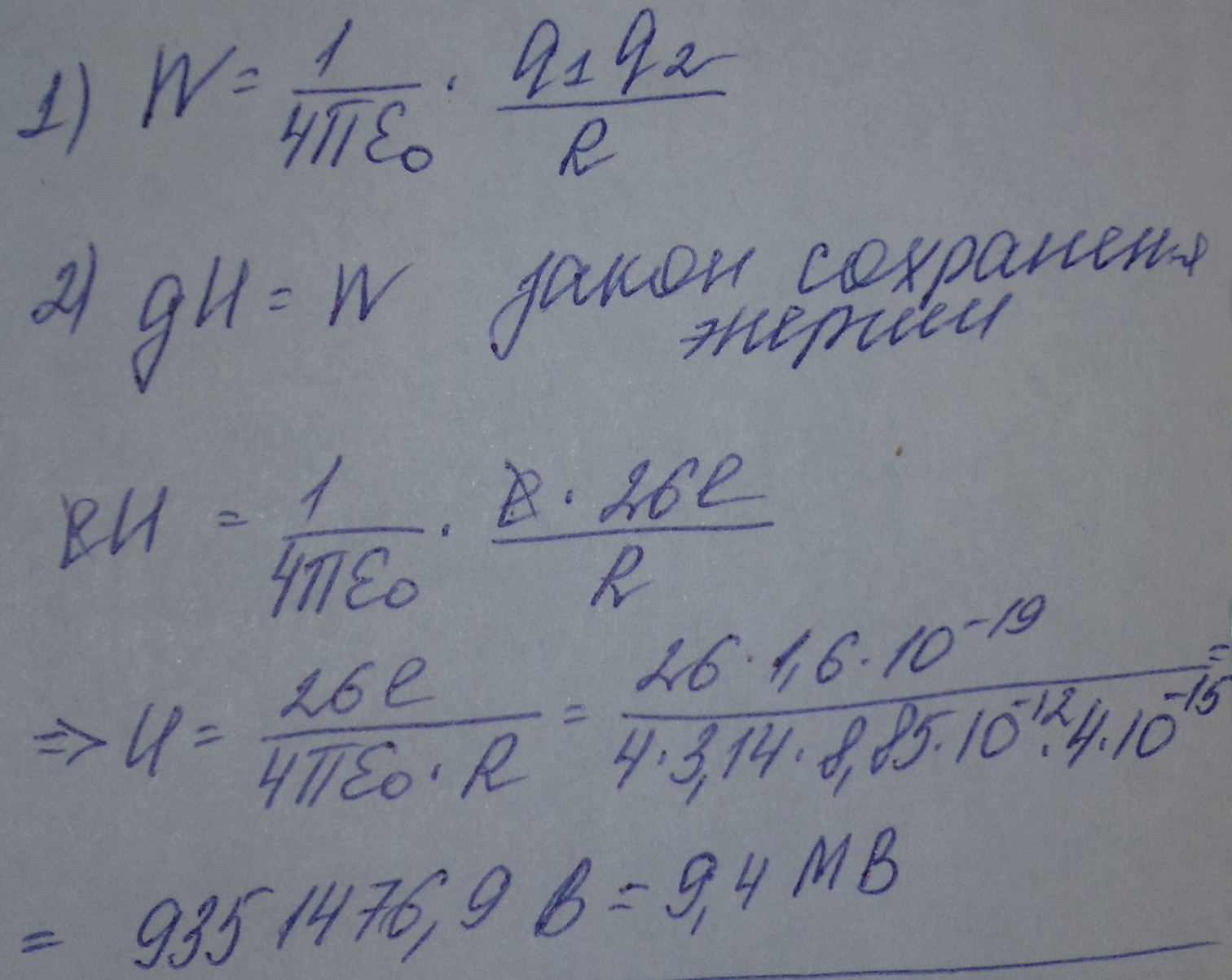




БИЛЕТ №5.

3.Определите энергию протона, который движется в однородном магнитном поле с индукцией B по винтовой линии радиусом R и шагом «винта» h.




V2-перпендикулярно,V1-параллельно,альфа-угол между скоростью и параллельной составляющей

eV2B=mV2^2/R

h=V1*T

T=2PiR/V2

Подставляем период в формулу для шага.выражаем оттуда тангенс.ищем угол.из формулы (1) находим скорость V2

V2=eBR/m=Vsin(альфа)

Отсюда ищем V подставив известный угол.Кинетическую энергию ищем по формуле.


4.Четыре равных точечных заряда Q расположены в вершинах квадрата со стороной b. а) Чему равна электрическая энергия системы? б) Какую потенциальную энергию будет иметь пятый заряд Q, помещенный в центре квадрата (относительно φ_∞=0 на бесконечности).

W=k* Q^2/b(1+…

ЗАРЯД В ЦЕНТРЕ ИМЕЕТ ПРОТИВОПОЛОЖНЫЙ ЗНАК

Второй раз энергия найдена неверно


БИЛЕТ №6.

3.На длинный соленоид, имеющий диаметр сечения d=5 см и содержащий n=20 витков на 1 см длины, плотно надет круговой виток из медного провода сечением S=1,0 мм2. Найти ток в витке, если ток в обмотке соленоида увеличивают с постоянной скоростью I = 100 А/С. Магнитным по­лем индукционного тока пренебречь. Удельное сопротивление меди ρ =16 нОм · м.



4.В модели атома водорода Бора электрон вращается вокруг ядра (протона) по круговой орбите радиусом r. Определите r, зная, что энергия ионизации (т.е. энергия, необходимая для отрыва электрона) по результатам измерения равна E_ион=-13,6 эВ.


БИЛЕТ №7.

3.На дифракционную решетку с периодом 2 мкм падает нормально свет, пропущенный сквозь светофильтр. Фильтр пропускает волны длиной от 500 до 600 нм. Будут ли спектры различных порядков накладываться друг на друга?

Запишем условие наложения двух соседних спектров k и (k+1) порядков для данных длин волн λ₂ и λ₁. Они должны быть видны под одним углом . Отсюда

.

Спектры данных линий могут перекрываться, начиная с k = 6. Определим максимальный порядок k_max, который дает данная решетка:

.

Для длины волны λ₁

.

Для длины волны λ₂

, (так как k целое число).

Следовательно, спектры длин волн λ₁ и λ₂ в данной решетке не перекрываются.
4.Провод с сопротивлением R=1,00 Ом растянули по длине втрое. Чему теперь равно его сопротивление?



3 l1=l2

R2=3 Ом

БИЛЕТ №8.

3.Какова линейная дисперсия дифракционной решетки для длины волны 0,589 мкм в спектре 2-го порядка, если постоянная решетки 4 мкм, а фокусное расстояние проецирующей линзы 50 см.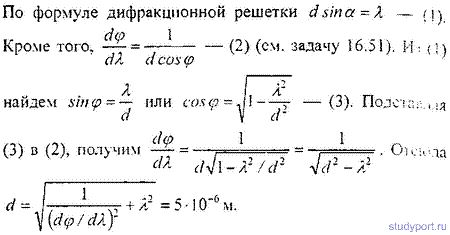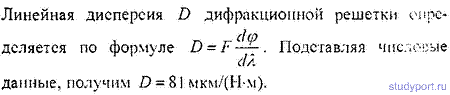


4. На тонкой нити длиной l =8см равномерно распределен заряд Q₁=350мкКл действующий силой F=120 мкН на точечный заряд Q₂ находящийся на продолжении той же нити на расстоянии r=6см от ее середины. Определить значение точечного заряда Q₂, если вся система находится в воздухе.


БИЛЕТ №9.

3. Расстояние между вторым и четвертым светлыми кольцами Ньютона в отраженном свете равно ∆r=0,9 мм. Определите радиус девятого темного кольца.


4. Определить потенциал электрического поля в центре кольца с внутренним радиусом R₁=20,9 см и внешним радиусом R₂=40см, если на нем равномерно распределен заряд Q=0,6 мкКл.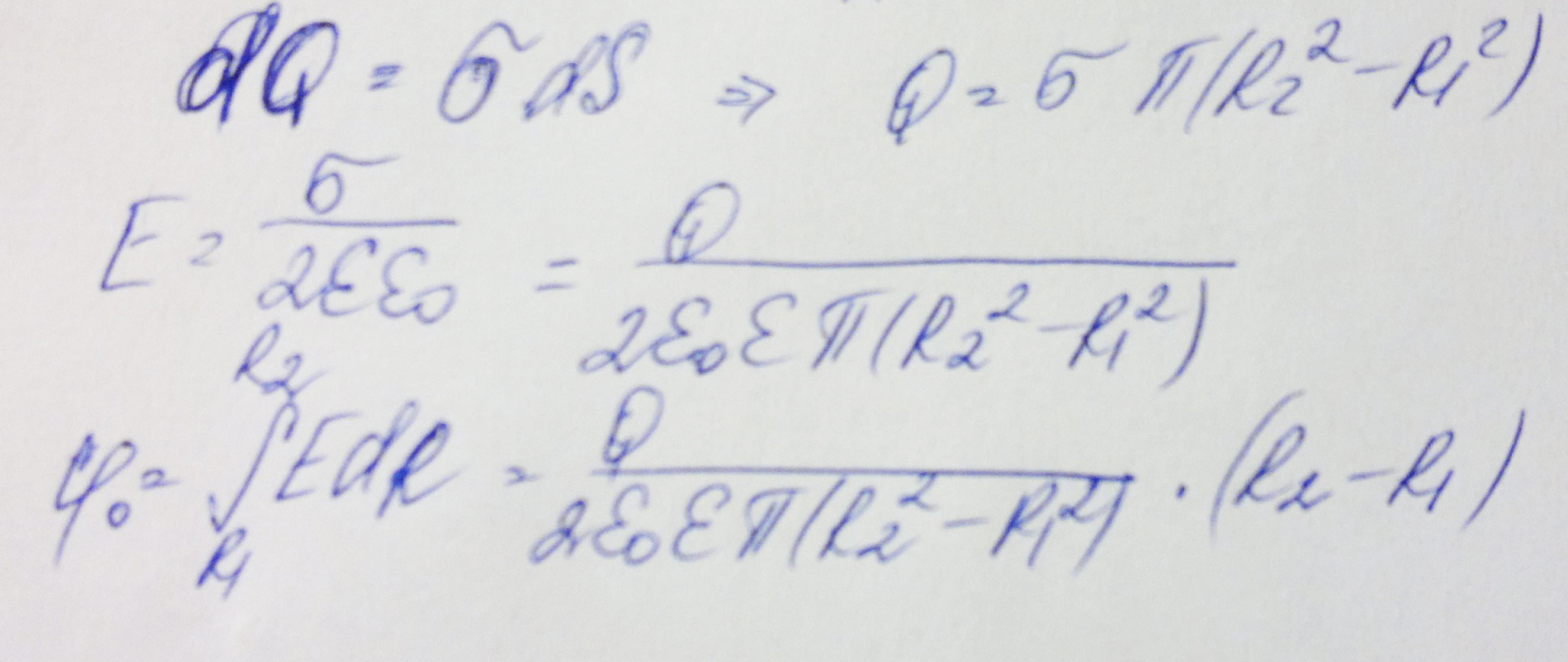


БИЛЕТ №10.

3.Магнитный поток через неподвижный контур с сопротивлением R изменяется в течение време­ни τ по закону Ф=αt(t-τ), где α - известная постоянная. Найти количество теплоты, выделившее­ся в контуре за это время. Магнитным полем индукционного тока пренебречь.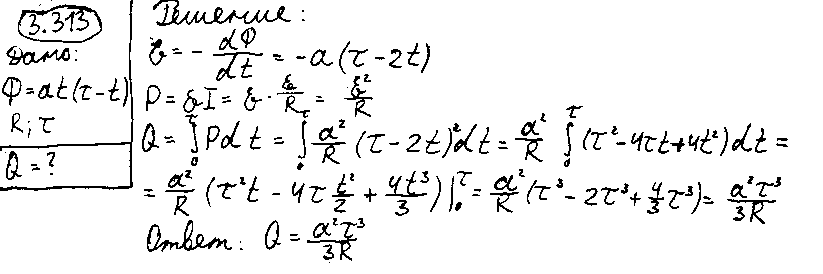



4.Бесконечная плоскость заряжена отрицательно с поверхностной плотностью σ=35,4нКл/м². По направлению силовой линии поля, созданного плоскостью, летит электрон. Определить мини­мальное расстояние l_min на которое может подойти к плоскости электрон, если на расстоянии l₀=5см он имел кинетическую энергию Т=80 эВ.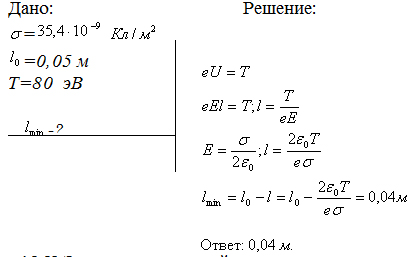


БИЛЕТ №11.

3. Провод, имеющий форму параболы y=кх², находится в однородном магнитном поле В, перпендикулярном плоскости Оху. Из вершины параболы перемещают поступательно и без началь­ной скорости проводящую перемычку (параллельную оси (Ох) с постоянным ускорением а. Найти ЭДС индукции в образовавшемся контуре, как функцию у.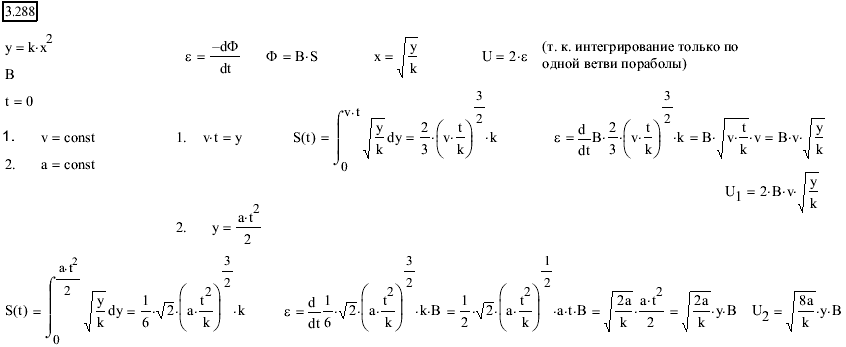





4. Определить заряд Q прошедший по проводу с сопротивлением R=3 Ом при равномерном нарастании напряжения на концах провода от U₀ =2B до U=4B в течение t=20 с.


БИЛЕТ №12.

3. Ток текущий по длинному прямому соленоиду, радиус сечения которого R, меняют так, что магнитное поле внутри соленоида возрастает со временем по закону В = βt², где β — постоянная. Найти плотность тока смещения как функцию расстояния г от оси соленоида.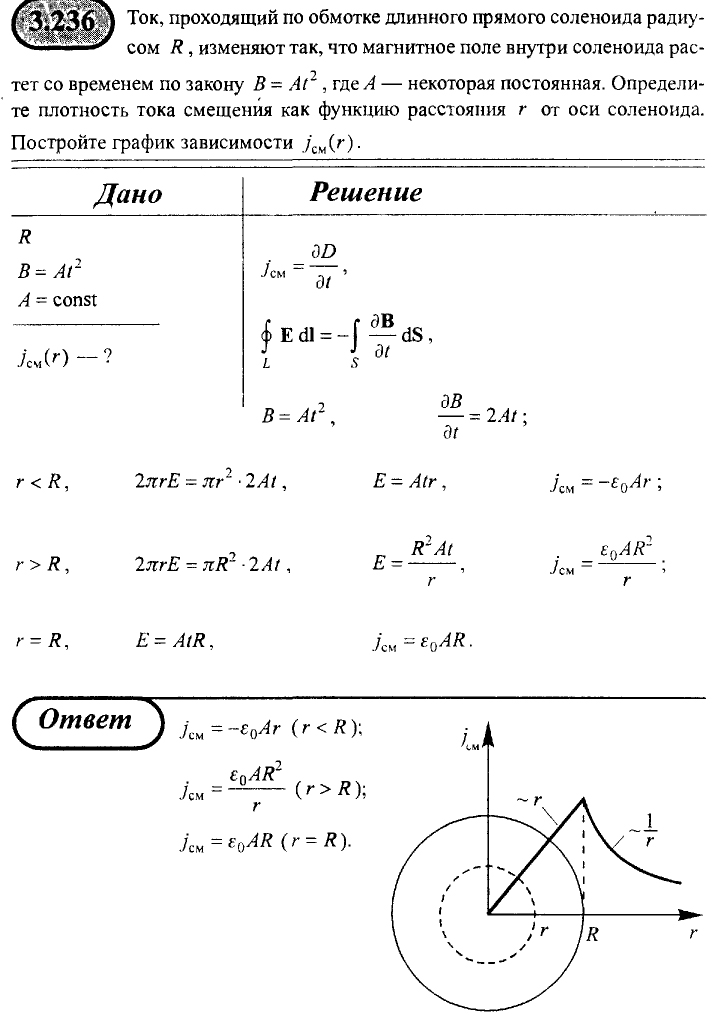



4. Система состоит из шара радиуса R, заряженного сферически - симметрично, и окружающей среды, заполненной зарядом с объемной плотностью ρ=α/г, где α - постоянная, г - расстояние от центра шара. Пренебрегая влиянием вещества, найти заряд шара, при котором модуль напряжен­ности электрического поля вне шара не зависит от r. Чему равна эта напряженность?


БИЛЕТ №13.

3.В длинном соленоиде с радиусом сечения α и числом витков n на единицу длины изменяют ток с постоянной скоростью I А/С. Найти напряженность вихревого электрического поля как функцию расстояния г от оси соленоида. Изобразить примерный график этой зависимости.


4.Пусть электрон, движущийся со скоростью ν₀=1,0 *10⁷ м/с (ν₀= ν₀i) влетает (x=y=0) в однородное электрическое поле Е, направленное под прямым углом к ν₀. Требуется найти уравнение траектории (y=y(x)) электрона в электрическом поле.
БИЛЕТ №14.

3.При нормальном падении света с длиной волны λ=450 нм на плоско-выпуклую линзу, находящуюся на плоской стеклянной поверхности, наблюдатель видит 33 светлых и 33 темных кольца Ньютона. Насколько линза толще в центре, чем по краям?
4.Внутри шара, заряженного равномерно с объемной плотностью ρ имеется сферическая полость. Центр полости смещен относительно центра шара на расстоянии а. Пренебрегая влиянием вещества шара, найти напряженность Е внутри полости.


БИЛЕТ №15.

3.В установке «кольца Ньютона» радиус выпуклой поверхности линзы равен R=0,9 м, а пространство между линзой и стеклянной пластинкой заполнено жидкостью. Чему равен показатель преломления жидкости, если при наблюдении в отраженном свете радиус второго светлого кольца r₂=0,75 мм,а длина волны света λ=0,65 мкм?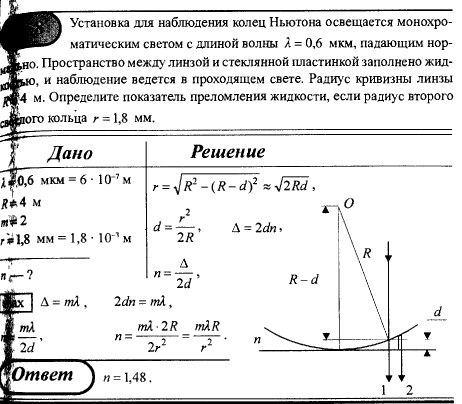





4.Электрический заряд Q равномерно распределен по объему непроводящего шара радиусом R. Определите напряженность электрического поля: а)снаружи шара (r>R); б)внутри шара (r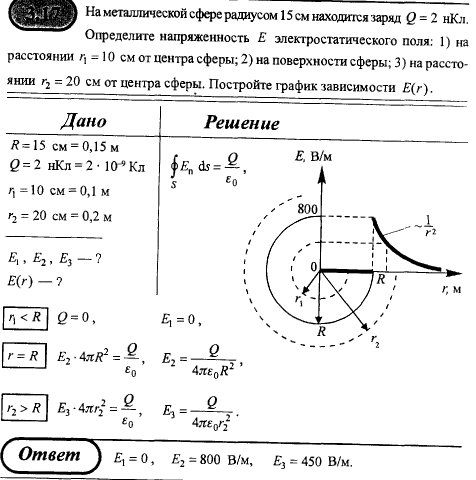


БИЛЕТ №16.

3.При сдвиге подвижного зеркала интерферометра Майкельсона наl=0,00275 см через поле зрения наблюдателя проходит N=100 интерференционных полос. Найти длину волны λ света, используемого в интерферометре.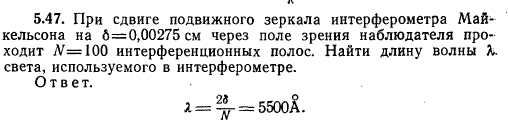






4.Кольцо массой m=5 10^-3 кг, радиусом R=5 10^-2 м с током I=2 А расположено горизонтально в магнитном поле, магнитная индукция которого меняется с высотой. Найдите градиент магнитного поля в точке, где кольцо находится в состоянии равновесия.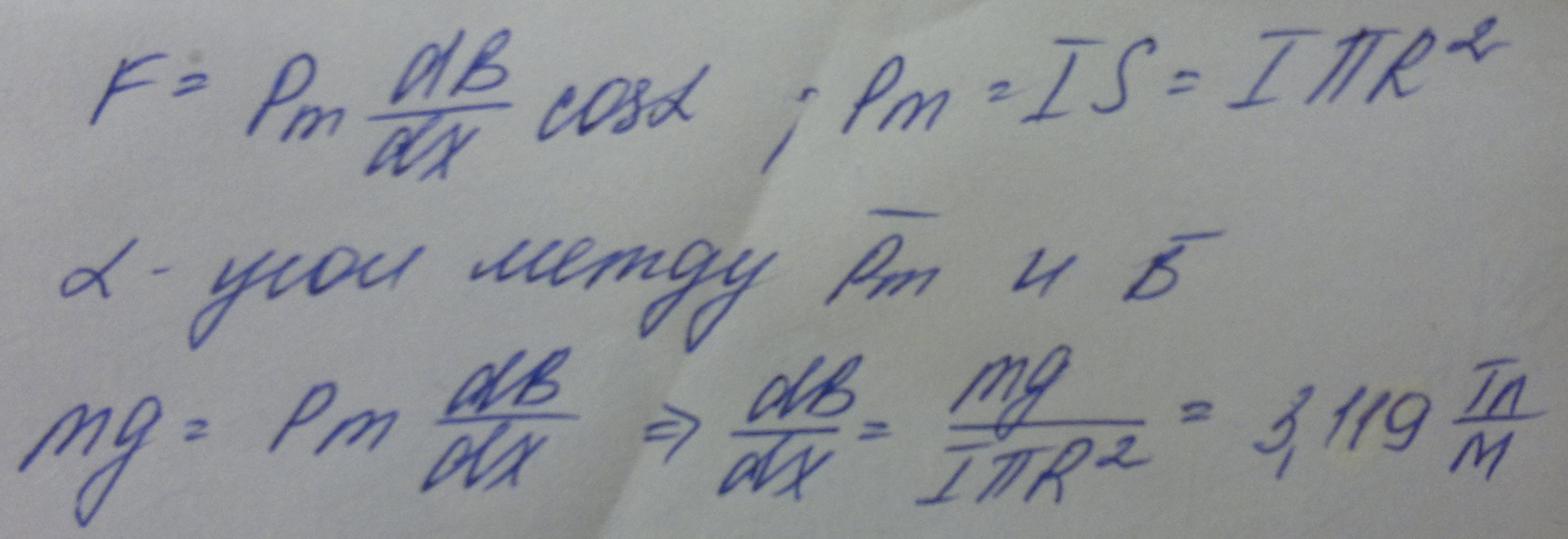




БИЛЕТ №17.

3.Принимая орбиту электрона в невозбужденном атоме водорода за окружность радиусом R=53 пм, определить магнитную индукцию поля, создаваемого в центре орбиты.



4.В опыте Юнга расстояние между соседними интерференционными максимумами на экране оказалось равным ∆y=0,5 мм. Определить длину волны падающего света, если расстояние между источниками d=3 мм, а расстояние от источника до экрана b=3 м.


БИЛЕТ №18.

3. На сферической оболочке радиусом R равномерно распределен заряд Q. Используя закон сохра­нения энергии,найти электрическую силу, приходящуюся на единицу площади оболочки.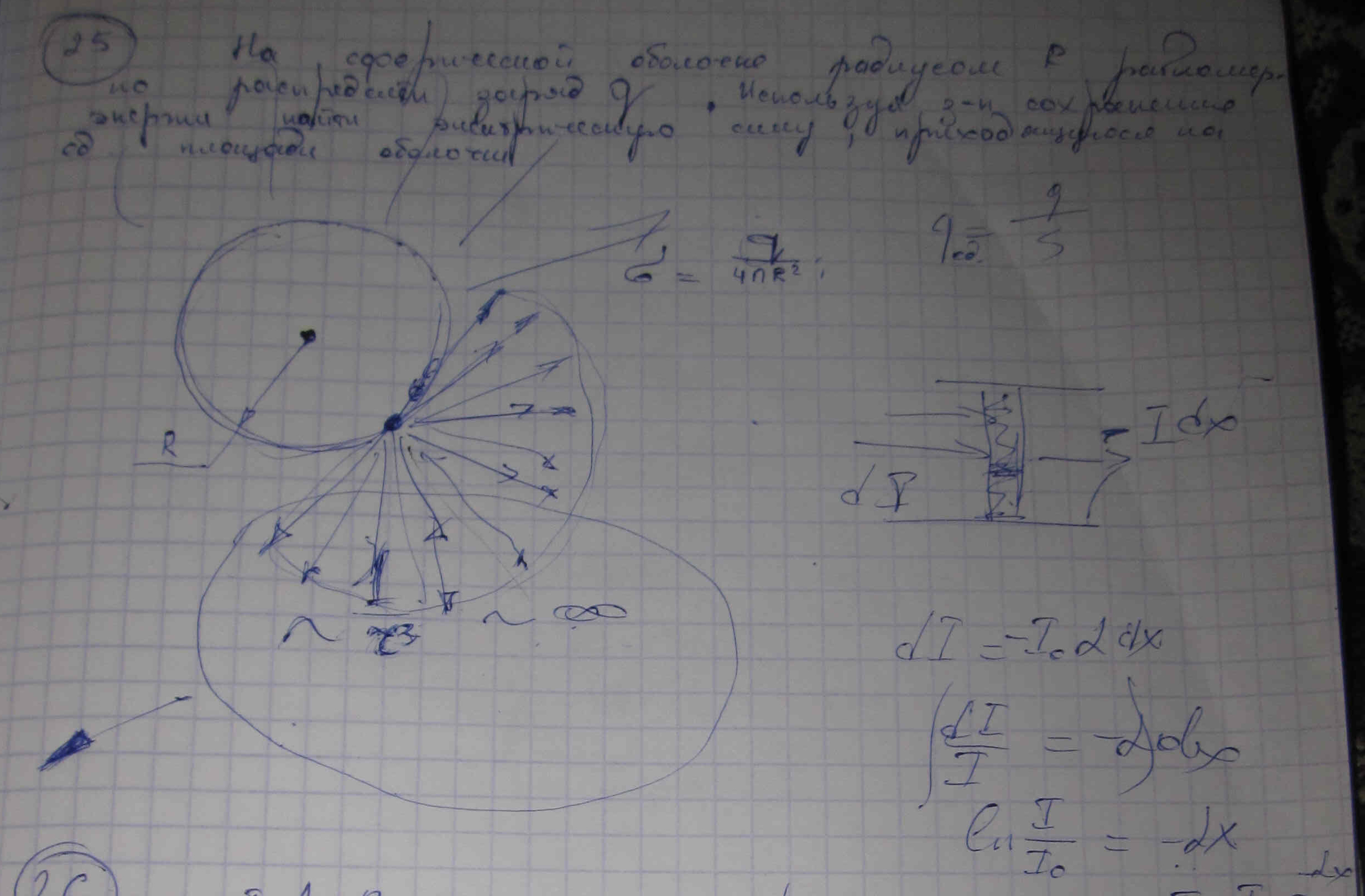


4.Определить магнитный момент электрона, движущегося по круговой орбите радиусом R=0,53 10^-10 м вокруг протона (боровская модель атома водорода).


БИЛЕТ №19.

3.Предельный угол полного внутреннего отражения для некоторого вещества равен γ=45º. Чему равен для этого вещества угол полной поляризации?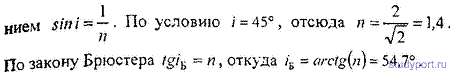



Ответ 54° 44'.
4.Какая энергия запасена на единице длины коаксиального кабеля с проводниками радиусами R₁ и R₂ (R₂>R₁), когда силы тока I в проводниках одинаковы и токи направлены в противопо­ложные стороны? Где плотность энергии максимальна?
БИЛЕТ №20.

3.В обмотке соленоида, сопротивление которой R=1,0 Ом и индуктивность L= 20 мГн, сила тока I₀=5,0A. Чему равна энергия магнитного поля соленоида через t = l,0 мc после отключения источ­ника?


4. Катушка диаметром D=25,0 см состоит из N=20 витков медной проволоки круглого сечения диаметром d=2,0мм. Однородное магнитное поле, перпендикулярное плоскости катушки, изменя­ется со скоростью dB/dt =6,55 10^-3 Тл/с. Определите:

а)силу тока в катушке;

б)выделяемую в катушке мощность.


БИЛЕТ №21.

3.К тонкому однородному проволочному кольцу радиусаR подводят токJ. Найти индукцию маг­нитного поля в центре кольца, если подводящие провода, делящие кольцо на две дуги длиной l₁ и l₂ расположены радиально и бесконечно длинные.

Решение. В основе этой задачи лежит формула для расчета магнитной индукции B₁ проводника с током I₁ длиной l₁, согнутым в виде дуги окружности радиуса r и подводящими проводами направленными строго радиально:

B1=μ04π⋅I1⋅l1r2(1)


(Монастырский Л.М. считает, что эту формулу вы должны знать или уметь выводить??).

Выберем направление тока так, как указано на рис. По правилу правой руки определяем направления магнитных индукций B₁ (к нам) и B₂ (от нас.). Тогда в проекции на ось Y, направленную к нам, из принципа суперпозиции полей получаем:

B_y = B₁ – B₂. (2)


Силы тока I₁ и I₂ найдем следующим образом. Участки l₁ и l₂  соединены параллельно, следовательно:

I₁ + I₂ = I, I₁⋅R₁ = I₂⋅R₂,


где R₁ = ρ⋅l₁/S — сопротивление участка длиной l₁. Аналогично для сопротивления R₂ = ρ⋅l₂/S. Тогда

I₁⋅l₁ = I₂⋅l₂ или (это можно не делать)
I1=I2⋅l2l1, I2⋅l2l1+I2=I, I2=I⋅l1l1+l2, I1=I⋅l2l1+l2.(3)


После подстановки уравнений (1) и (3) в (2) получаем
 

By=μ04π⋅r2⋅(l1⋅I1−l2⋅I2)=0.
4.Покажите, что индуктивность тора с прямоугольным сечением дается формулой

L=µ₀ N² h ln(R₂/R₁)/(2π), где N-полное число витков, h-высота стороны сечения, R₁ и R₂-соответственно внутренний и внешний радиусы тора.


БИЛЕТ №22.

3.Сферический слой образованный концентрическими сферами из идеального проводника, заполнен веществом с электропроводностью γ. Чему равно сопротивление R этого слоя, если его внутренний радиус R₁, внешний – R₂?


4.На электрон, движущийся в магнитном поле B=0,72 к Тл, действует сила F=(3,2 i – 2,7 j) 10^-13 Н. Чему равна скорость электрона?
БИЛЕТ №23.

3.В вакууме распространяется плоская гармоническая линейно поляризованная электромагнитная волна частоты ω. Интенсивность волны равна I. Найти амплитудное значение плотности тока смещения в этой волне.


4.Покажите, что магнитный момент p_m электрона, движущегося по орбите вокруг протона в атоме водорода, связан с орбитальным моментом импульса Lэлектрона соотношением p_m=eL/(2m).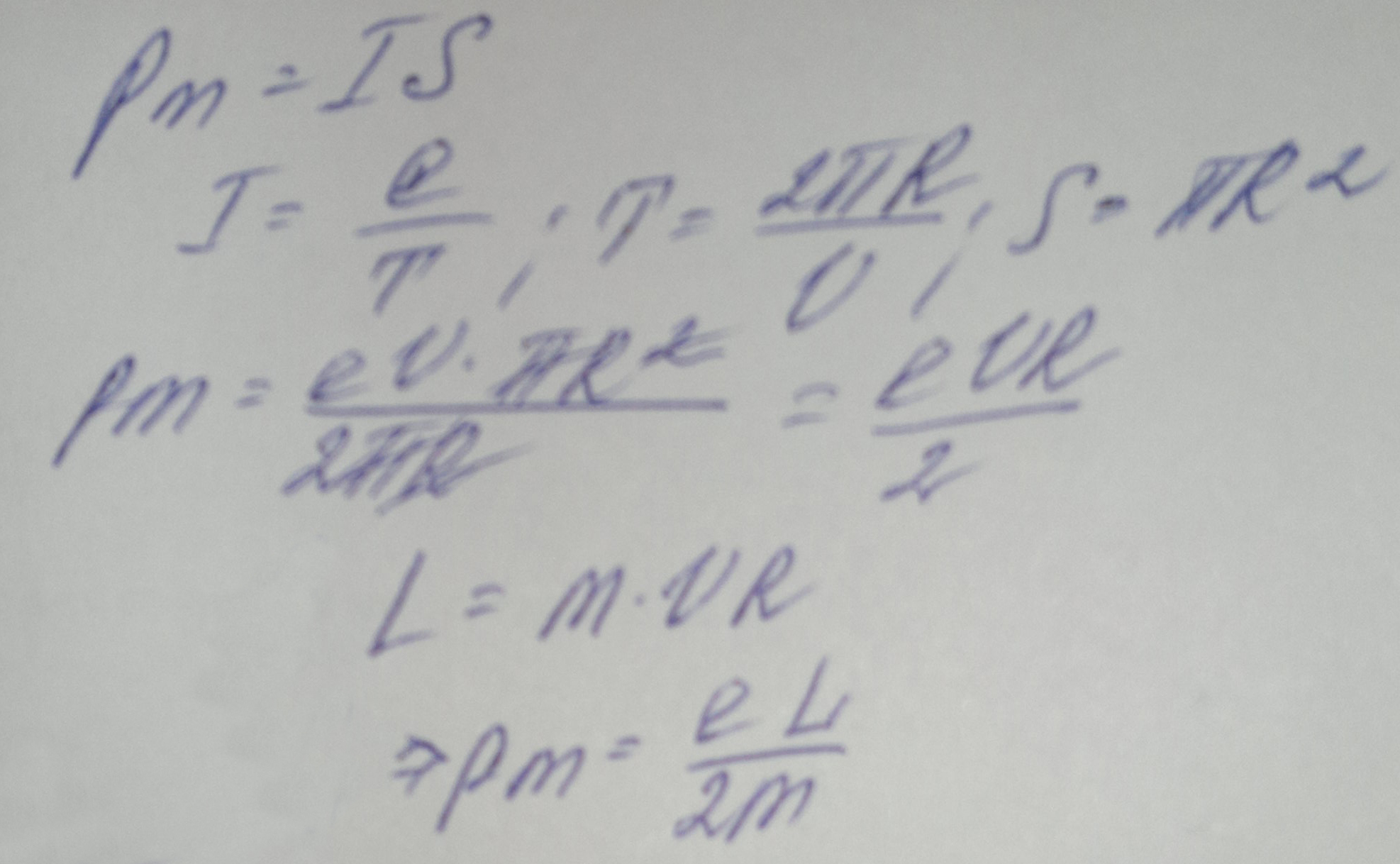


БИЛЕТ №24.

3.Радиус длинного парамагнитного сердечника соленоида R=1,0 см. Соленоид содержит n=10 витков на 1см длины. Обмотка выполнена из медного провода сечением S=1,0 мм². Через какое время в обмотке соленоида выделится количество теплоты, равное энергии магнитного поля в сердечнике, если она подключена к источнику постоянного напряжения? Удельное сопротивление меди ρ=16 нОм м.

2. Пусть соленоид таков, что его длина много больше диаметра сердечника. Выделим в соленоиде вдали от его краев элемент длины
l = 1 см = 0,01 м, обмотка которого содержит n = 10 витков. Индуктивность такого элемента
L = μμ₀n²S/l = πμμ₀n²r²/l,
где S – площадь поперечного сечения, r – радиус сердечника;
энергия магнитного поля в сердечнике при I = const
W = LI²/2 = πμμ₀n²r²I²/l. (1)

Предположим, что обм отка соленоида выполнена из проволоки круглого сечения. Тогда при площади поперечного сечения a = 1 см² = 1 ∙ 10^-4 м² радиус сечения провода равен
c = V(a/π) = V((1 ∙ 10^-4/π) 0,564 ∙ 10^-2 (м).
Диаметр сечения провода составляет тогда d = 2c = 2 ∙ 0,564 ∙ 10^-2 1,13 ∙ 10^-2 (м), и на длине l = 0,01 м десять витков уложены быть не могут. Поэтому ограничимся предположением о том, что обмотка выполнена плотно, т. е. витки проволоки уложены без зазоров, форма сечения проволоки неизвестна, а длина проволоки b приблизительно равна произведению числа витков на длину периметра поперечного сечения сердечника, т. е.
b 2πrn.
Сопротивление обмотки
R = ρb/a;
количество теплоты, выделившейся в обмотке,
Q = I²Rt = I²tρb/a. (2)

По условию задачи Q = W. Тогда, приравнивая в ыражения (1) и (2), получаем
I²tρb/a = πμμ₀n²r²I²/l,
tρb/a = πμμ₀n²r²/l,
откуда выводим
t = πμμ₀n²r²a/(lρb) = πμμ₀n²r²a/(2πrnlρ) = μμ₀nra/(2lρ). (3)

Подставим в формулу (3) числовые значения величин: μ > 1 (для парамагнетика), μ₀ = 4π ∙ 10^-7 Гн/м, n = 10,
r = 0,01 м, a = 1 ∙ 10^-4 м², l = 0,1 м, ρ = 1,72 ∙ 10^-8 Ом ∙ м и найдем
t > 4π ∙ 10^-7 ∙ 10 ∙ 0,01 ∙ 1 ∙ 10^-4/(2 ∙ 0,1 ∙ 1,72 ∙ 10^-8) 3,65 ∙ 10^-3 (с).
Поскольку материал парамагнетика в условии не указан, точное значение врем ени определить невозможно.

Ответ: t > 3,65 ∙ 10^-3 с.
4.По длинному горизонтальному проводнику течет ток I1=78 А. Второй медный проводник диаметром d=3,5 мм удерживается магнитными силами параллельно первому на расстоянии l=18 см под ним:

а)Какова сила и направление тока во втором проводнике?

б)Находится ли второй проводник в устойчивом равновесии?
Противоположно направлена, т.к.они отталкиваются


БИЛЕТ №25.

3.Плосковыпуклая линза, радиус кривизны сферической поверхности которой R соприкасается со стеклянной пластинкой. Оцените радиус наблюдаемой в отражении свете интерференционной картины и число видимых колец, если длина волны света λ и ∆λ. Свет падает почти нормально.




4.Ток I течет по длинному прямому проводнику круглого сечения с магнитной проницаемостью µ. Найти энергию магнитного поля внутри провода в расчете на единицу его длины.


БИЛЕТ №26.

3.Плоская световая волна с λ=0,64 мкм и интенсивностью I₀ падает нормально на круглое отверстие радиуса r=1,2 мм. Найти интенсивность в центре дифракционной картины на экране, отстоящем от отверстия на расстоянии b=1,5 м.
4.В установке для наблюдения колец Ньютона в отраженном свете расстояние между третьим и пятым темными кольцами оказалось равным ∆r=0,5 мм. Определите радиус линзы, если длина волны излучения λ=0,6 мкм.


БИЛЕТ №27.

3.При изготовлении полиэтиленовая пленка прокатывается между валками, образуя тонкую ленту шириной L, и при этом электризуется. Найдите магнитную индукцию поля в точке, расположенной в одной плоскости с лентой на расстоянии d от нее. Скорость движения ленты V, поверхностная плотность заряда σ.


4.В однородном магнитном поле с индукцией B=0,8 Тл помещена тонкая медная пластина, в которой сила тока I=5,0 А. Вектор индукции магнитного поля перпендикулярен плоскости пластины. Толщина пластины δ=0,01 м. Определить концентрацию свободных электронов в меди, если возникшая вдоль ширины пластины разность потенциалов ∆φ=2,0 мкВ.


БИЛЕТ №28.

3. Точки А и В находятся на одной прямой (АВ = 2м). В точке А находится точечный источник монохроматического света (λ = 500 нм). Диафрагма с отверстием радиусом 1 мм перемещается из точки, отстоящей от А на 50см, в точку, отстоящую от А на 1,5м. Сколько раз будет наблюдаться затемнение в точке В?



4. Виток радиусом R=10 см, по которому течёт постоянный ток I = 20А, помещён в магнитное поле с индукцией В = 1 Тл так, что его нормаль образует с вектором магнитной индукции угол α=60º. Определить работу, которую нужно совершить против магнитных сил, чтобы удалить виток из поля.