Практические занятия по теме 9. Решение Используем формулу расчета будущей стоимости способом сложных процентов современная стоимость
 Скачать 20 Kb. Скачать 20 Kb.
|
|
Практические занятия по теме 9. 1. Решение задач. 1. Стоимость земельного участка, купленного за 15 тыс. руб., ежегодно увеличивается на 14%. Сколько будет стоить участок через 4 года после приобретения? Решение Используем формулу расчета будущей стоимости способом сложных процентов: 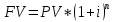 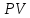 – современная стоимость – современная стоимость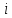 – процентная ставка – процентная ставка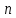 – количество периодов начисления – количество периодов начисленияБудущая стоимость участка составит: 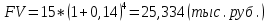 Ответ: 25,334 тыс. руб. 2. Какую сумму целесообразно заплатить инвестору за объект недвижимости, который можно эффективно эксплуатировать 5 лет? Объект в конце каждого года приносит доход по 350 тыс. руб. Требуемый доход на инвестиции - 20%. Решение Определим современную стоимость ежегодных поступлений от эксплуатации объекта: 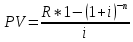 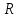 – размер ежегодного платежа. – размер ежегодного платежа.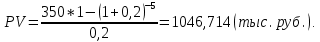 Ответ: сумма в оплату объекта недвижимости не должна превышать 1046,714 тыс. руб. 3. Рассчитайте текущую стоимость потока арендных платежей, возникающих в конце года, если годовой арендный платеж первые четыре года составляет 400 тыс. руб., затем он уменьшится на 150 тыс. руб. и сохранится в течение трех лет, после чего возрастет на 350 тыс. руб. и будет поступать еще два года. Ставка дисконта - 10%. Решение Современная стоимость потока арендных платежей составит: 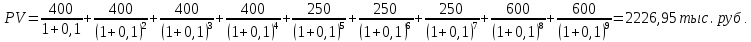 Ответ: текущая стоимость равна 2226,95 тыс. руб. 4. Объект в течение восьми лет обеспечит в конце года поток арендных платежей по 280 тыс. руб. После получения последней арендной платы он будет продан за 11500 тыс. руб. Расходы по продаже составят 500 тыс. руб. Рассчитайте совокупную текущую стоимость предстоящих поступлений денежных средств, если вероятность получения запланированной суммы аренды и продажи требует применения ставок дисконта в 10 и 20% соответственно. Решение Современная стоимость потока арендных платежей составит: 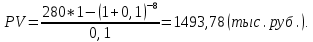 Современная стоимость продажи составит: 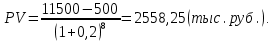 Cовокупная текущая стоимость предстоящих поступлений: 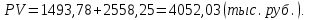 5. Рассчитайте суммарную будущую стоимость денежного потока, накапливаемого под 8%. Денежный поток возникает в конце года. Первый год - 100 тыс. руб. Второй год - 800 тыс. руб. Третий год- 0. Четвертый год - 300 тыс. руб. Решение Будущая стоимость потока платежей составит:  6. Рассчитайте текущую стоимость потока арендных платежей, возникающих в конце года, если годовой арендный платеж первые четыре года составляет 400 тыс. руб., затем он уменьшится на 150 тыс. руб. и сохранится в течение трех лет, после чего возрастет на 350 тыс. руб. и будет поступать еще два года. Ставка дисконта - 10%. Решение Современная стоимость потока арендных платежей составит:  Ответ: текущая стоимость равна 2226,95 тыс.руб. 7. Объект в течение восьми лет обеспечит в конце года поток арендных платежей по 280 тыс. руб. После получения последней арендной платы он будет продан за 11500 тыс. руб. Расходы по продаже составят 500 тыс. руб. Рассчитайте совокупную текущую стоимость предстоящих поступлений денежных средств, если вероятность получения запланированной суммы аренды и продажи требует применения ставок дисконта в 10 и 20% соответственно. Решение Современная стоимость потока арендных платежей составит:  Современная стоимость продажи составит:  Cовокупная текущая стоимость предстоящих поступлений:  8. Рассчитайте ежегодный платеж в погашение кредита в сумме 300 тыс. руб., выданного на пять лет под 28%. Решение Для расчета ежегодного платежа используем формулу:  Ежегодный платеж составит:  Ответ: ежегодный платеж в счет погашения кредита равен 118 483 руб. 9. Рассчитайте текущую стоимость обыкновенной акции ПАО «Суперсталь», если ожидается, что дивиденды компании будут постоянно расти на 5% в год, если дивиденды этого года равны 10 руб. на одну акцию, а ставка рыночной капитализации 8%. Решение Стоимость акции составит:  Ответ: стоимость акции равна 350 руб. 10. Определите ставку дисконта, используя модель оценки капитальных активов, если известны следующие данные: безрисковая ставка дохода – 10 %, коэффициент бета - 1,2, средняя доходность на сегменте рынка – 18 %, премия для малых предприятий – 3 %, премия за риск для конкретной фирмы – 2%. Решение В соответствии с моделью капитальных активов (CAPM) ставка дисконтирования определяется по формуле:  R -ставка дисконта; Rf - безрисковая ставка; β -коэффициент «бета»; Rm -общая доходность рынка в целом;  - премия для малых компаний; - премия для малых компаний; - премия за риск инвестиций в конкретную компанию; - премия за риск инвестиций в конкретную компанию; Ответ: ставка дисконта, определенная по модели оценки капитальных активов, равна 24,6% 11. Определите стоимость предприятия (бизнеса) в постпрогнозный период, используя модель Гордона, если известны следующие исходные данные: денежный поток в первый год постпрогнозного периода – 3750 тыс. руб., ставка дисконта – 28 %, долгосрочные темпы роста денежного потока – 3%. Решение В соответствии с моделью Гордона стоимость предприятия в постпрогнозный год определяется по формуле:  Vост - стоимость компании в постпрогнозный период; Дпост - денежный поток в первый год постпрогнозного периода; g - долгосрочные темпы роста денежного потока; R - ставка дисконтирования. Стоимость предприятия в постпрогнозный период будет равна:  Ответ: стоимость предприятия в постпрогнозный период составляет 15 000 тыс. рублей. 12. Номинальная ставка дохода по государственным облигациям составляет 25%. Среднерыночная доходность на фондовом рынке - 19% в реальном выражении. Коэффициент бета для оцениваемого предприятия равен 1,4. Темпы инфляции составляют 16% в год. Рассчитайте реальную ставку дисконта для оцениваемого предприятия. Решение Определим реальную ставку доходности по безрисковым активам с учетом инфляции по формуле Фишера   - реальная ставка; - реальная ставка; - номинальная ставка; - номинальная ставка; - темп инфляции - темп инфляции Реальная ставка дисконта составит:  13. Рассчитайте текущую стоимость предприятия в постпрогнозный период, используя модель Гордона, если денежный поток в постпрогнозный период равен 900 млн руб., ожидаемые долгосрочные темпы роста - 2%, ставка дисконта - 18%. Решение В соответствии с моделью Гордона стоимость предприятия в постпрогнозный год определяется по формуле:  Vост - стоимость компании в постпрогнозный период; Дпост - денежный поток в первый год постпрогнозного периода; g - долгосрочные темпы роста денежного потока; R - ставка дисконтирования. Стоимость предприятия в постпрогнозный период будет равна:  Ответ: стоимость предприятия в постпрогнозный период составляет 5625 млн. рублей. 14. В конце каждого из последующих четырех лет фирма предполагает выплачивать дивиденды в размере: 2 долл., 1,5 долл., 2,5 долл., 3,5 долл. Какую цену вы готовы заплатить за акцию данной фирмы, если ожидается, что в дальнейшем дивиденды будут расти на 5% в год, а требуемая ставка дохода составляет 19%? Решение Определим дисконтированную величину дивидендов в прогнозный период. Современная величина дивидендов в 1-4 годы составит:     Для определения величины дивиденда в постпрогнозный период используем формулу Гордона:   денежный поток за первый год постпрогнозного периода; денежный поток за первый год постпрогнозного периода;q - долгосрочные темпы роста$  – ставка дисконтирования. – ставка дисконтирования. Дисконтированная величина остаточной стоимости составит:  Цена акции равна сумме текущих стоимостей всех будущих доходов:  15. Оценочная стоимость активов предприятия составляет 22 000 долл. Для его ликвидации потребуется полтора года. Затраты на ликвидацию составляют 25% стоимости активов. Какова текущая стоимость выручки от продажи при ставке дисконта 18%? Решение Рассчитаем остаточную стоимость активов с учетом затрат на ликвидацию: ОС = Оценочная стоимость – Затраты на ликвидацию = 22000 – 22000 * 0,25 = 16500 долл. Дисконтируем остаточную стоимость активов к текущему моменту времени и рассчитаем выручку от продажи предприятия:  Ответ: текущая выручка от продажи предприятия равна 12 872 долл. 16. При оценке стоимости компании ПАО «Мегафон» наиболее приближенной к справедливой/рыночной цене будет сумма расчета по сравнительному подходу, поскольку существуют компании-аналоги, сопоставимые по объемам бизнеса и характеру деятельности (ПАО МТС, ВымпелКом, Теле 2). |
