Площадь фигуры по ограниченным кривым. Вычислить площадь фигуры ПРИМЕРЫ. Решение. Из уравнения эллипса для i квадранта имеем. Отсюда по формуле получаем
 Скачать 349.26 Kb.
|
|
Вычислить площадь фигуры, ограниченной линиями    .Решение. Находим точки пересечения заданных линий. Для этого решаем систему уравнений: 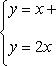 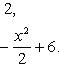 Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:   или  .Находим: x1 = -2, x2 = 4. Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6). 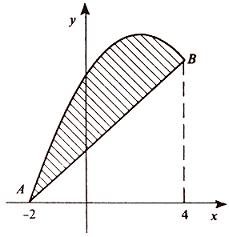 Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле: 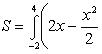 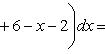 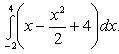 По формуле Ньютона-Лейбница находим: 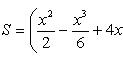 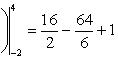 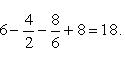 Найти площадь области, ограниченной эллипсом  .Решение. 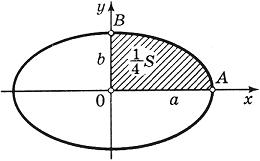 Из уравнения эллипса для I квадранта имеем   . Отсюда по формуле  получаем   Применим подстановку x = a sin t, dx = a cos tdt. Новые пределы интегрирования t = α и t = β определяются из уравнений 0 = a sin t, a = a sin t. Можно положить α = 0 и β = π/2. Находим одну четвертую искомой площади          Отсюда S = πab. Найти площадь фигуры, ограниченной линиямиy= -x2+x+ 4 иy= -x+ 1. Решение. Найдем точки пересечения линий y = -x2 + x + 4, y = -x + 1, приравнивая ординаты линий: -x2 + x + 4 = -x + 1 или x2 - 2x - 3 = 0. Находим корни x1 = -1, x2 = 3 и соответствующие им ординаты y1 = 2, y2 = -2. 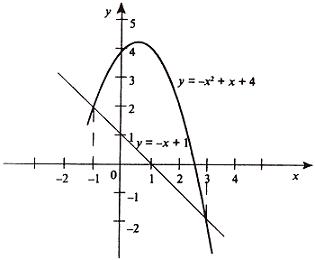 По формуле площади фигуры получаем 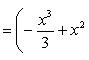 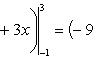 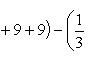 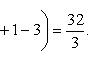     Определить площадь, ограниченную параболойy=x2+ 1 и прямойx+y= 3. Решение. Решая систему уравнений   находим абсциссы точек пересечения x1 = -2 и x2 = 1. 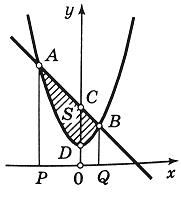 Полагая y2 = 3 - x и y1 = x2 + 1, на основании формулы 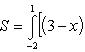 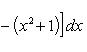 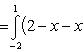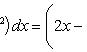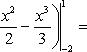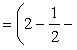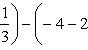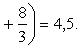получаем        Вычислить площадь, заключенную внутри лемнискаты Бернуллиr2=a2cos 2φ. Решение. 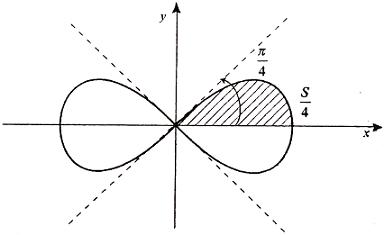 В полярной системе координат площадь фигуры, ограниченной дугой кривой r = f(φ) и двумя полярными радиусами φ1 = ʅ и φ2 = ʆ, выразится интегралом   В силу симметрии кривой определяем сначала одну четвертую искомой площади 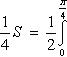  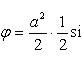 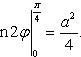 Следовательно, вся площадь равна S = a2. Вычислить длину дуги астроидыx2/3+y2/3=a2/3. Решение. 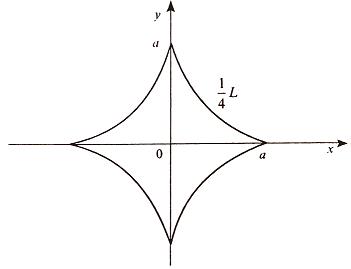 Запишем уравнение астроиды в виде (x1/3)2 + (y1/3)2 = (a1/3)2. Положим x1/3 = a1/3cos t, y1/3 = a1/3sin t. Отсюда получаем параметрические уравнения астроиды x = a cos3t, y = a sin3t, (*) где 0 ≤ t ≤ 2π. Ввиду симметрии кривой (*) достаточно найти одну четвертую часть длины дуги L, соответствующую изменению параметра t от 0 до π/2. Получаем dx = -3a cos2t sin t dt, dy = 3a sin2t cos t dt. Отсюда находим    Интегрируя полученное выражение в пределах от 0 до π/2, получаем      Отсюда L = 6a. Найти площадь, ограниченную спиралью Архимедаr=aφи двумя радиусами-векторами, которые соответствуют полярным угламφ1иφ2(φ1<φ2). Решение. 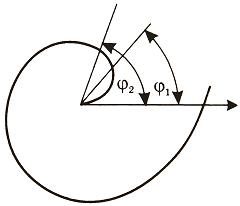 Площадь, ограниченная кривой r = f(φ) вычисляется по формуле   , где α и β - пределы изменения полярного угла.Таким образом, получаем 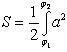 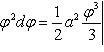 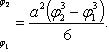 (*)Из (*) следует, что площадь, ограниченная полярной осью и первым витком спирали Архимеда (φ1 = 0; φ2 = 2π):   Аналогичным образом находим площадь, ограниченную полярной осью и вторым витком спирали Архимеда (φ1 = 2π; φ2 = 4π):    Искомая площадь равна разности этих площадей    Вычислить объем тела, полученного вращением вокруг осиOxфигуры, ограниченной параболамиy=x2иx=y2. Решение. 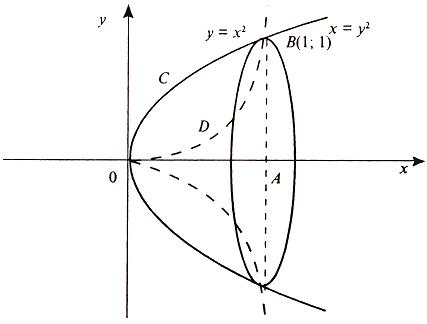 Решим систему уравнений  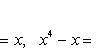 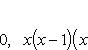 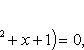 и получим x1 = 0, x2 = 1, y1 = 0, y2 = 1, откуда точки пересечения кривых O(0; 0), B(1; 1). Как видно на рисунке, искомый объем тела вращения равен разности двух объемов, образованных вращением вокруг оси Ox криволинейных трапеций OCBA и ODBA: 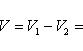 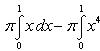 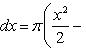  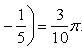 Вычислить площадь, ограниченную осьюOxи синусоидойy= sinxна отрезках: а) [0,π]; б) [0, 2π]. Решение. 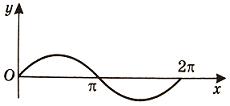 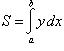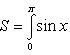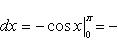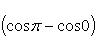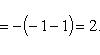а) На отрезке [0, π] функция sin x сохраняет знак, и поэтому по формуле  , полагая y = sin x, находим    б) На отрезке [0, 2π], функция sin x меняет знак. Для корректного решения задачи, необходимо отрезок [0, 2π] разделить на два [0, π] и [π, 2π], в каждом из которых функция сохраняет знак. По правилу знаков, на отрезке [π, 2π] площадь берется со знаком минус. В итоге, искомая площадь равна         Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса вокруг б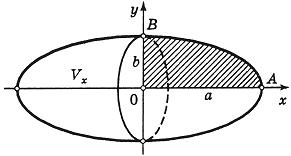ольшой осиa.Решение.  Учитывая, что эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси Oxплощади OAB, равной одной четверти площади эллипса, и полученный результат удвоить. Обозначим объем тела вращения через Vx; тогда на основании формулы 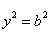 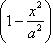 имеем   , где 0 и a - абсциссы точек B и A. Из уравнения эллипса находим   . Отсюда        Таким образом, искомый объем равен  . (При вращении эллипса вокруг малой оси b, объем тела равен  )Найти площадь, ограниченную параболамиy2= 2pxиx2= 2py. Решение. 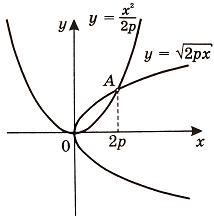 Сначала найдем координаты точек пересечения парабол, чтобы определить отрезок интегрирования. Преобразуя исходные уравнения, получаем  и  . Приравнивая эти значения, получим  или x4 - 8p3x = 0.Отсюда x4 - 8p3x = x(x3 - 8p3) = x(x - 2p)(x2 + 2px + 4p2) = 0. Находим корни уравнений:          Учитывая то факт, что точка A пересечения парабол находится в первой четверти, то пределы интегрирования x = 0 и x = 2p. Искомую площадь находим по формуле 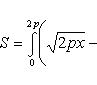 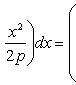 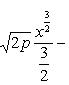 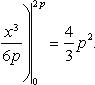   |