Задания по курсачу матан. Исследование и построить график функции Построить график функции в полярной системе координат
 Скачать 2.8 Mb. Скачать 2.8 Mb.
|
    1. Варианты контрольных заданий по дифференциальному исчислению. 1. Варианты контрольных заданий по дифференциальному исчислению.Вариант 1 1. Вычислить пределы с помощью правила Лопиталя: а) 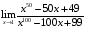 ; б) ; б) 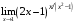 2. Провести исследование и построить график функции:  . .3. Построить график функции в полярной системе координат 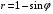 . . 4. Найти стороны 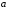 и и 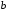 прямоугольника, вписанного в окружность единичного прямоугольника, вписанного в окружность единичного радиуса и имеющего среди всех таких прямоугольников наибольшую площадь. 5. Вычислить 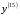 функции функции  . .6. Используя формулу Тейлора 2 - го порядка, вычислить приближенно 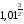 и идоказать, что при этом погрешность  допускает нижеследующую оценку: допускает нижеследующую оценку:  7. Составить уравнения касательной и нормали к кривой  в точке в точке 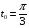 и вычислить и вычислить  . .8. Вычислить производную 2-го порядка от неявной функции: 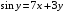 . .9. Вычислить предел с помощью формулы Тейлора:  . . 10. Известно, что  для всех для всех  . Существуют ли еще какие-нибудь . Существуют ли еще какие-нибудь функции, совпадающие со своими производными всюду? 11. По графику функции построить график ее первой производной 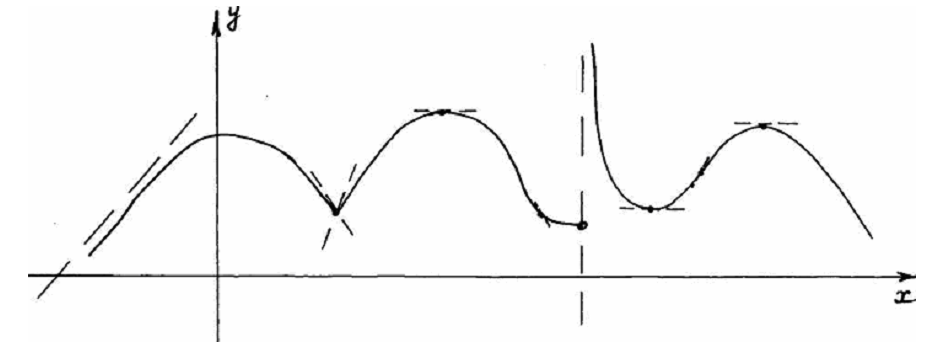 Вариант 2 1. Вычислить пределы с помощью правила Лопиталя: а)  ; б) ; б) 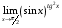 . .2. Провести исследование и построить график функции:  . .3. Построить график функции в полярной системе координат 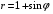 . . 4. В трапеции три стороны имеют длину 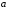 . Какую длину должна иметь четвертая . Какую длину должна иметь четвертая сторона, чтобы площадь была максимальной? 5. Вычислить  функции функции  . .6. Используя формулу Тейлора  го порядка, вычислить приближенно значение го порядка, вычислить приближенно значение  и доказать, что при этом погрешность и доказать, что при этом погрешность  допускает нижеследующую допускает нижеследующую оценку:  . . 7. Составить уравнения касательной и нормали к кривой 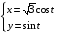 в точке в точке 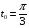 и вычислить и вычислить  . .8. Вычислить производную 2-го порядка от неявной функции:  . .9. Вычислить предел с помощью формулы Тейлора:  . .10. В формуле Лагранжа определить значение  для функции для функции 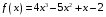 на отрезке на отрезке 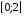 . . 11. По графику функции построить график ее первой производной  Вариант 3 1. Вычислить пределы с помощью правила Лопиталя: а) 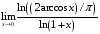 ; б) ; б)  . .2. Провести исследование и построить график функции:  . .3. Построить график функции в полярной системе координат 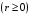  . . 4. Найти радиус основания  и образующую и образующую 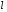 прямого кругового конуса, прямого кругового конуса, вписанного в сферу единичного радиуса и имеющего среди таких конусов наибольшую полную поверхность. 5. Вычислить  функции функции 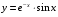 . .6. Используя формулу Тейлора  го порядка, вычислить приближенно значение го порядка, вычислить приближенно значение и доказать, что при этом погрешность и доказать, что при этом погрешность  допускает нижеследующую допускает нижеследующую оценку:  . . 7. Составить уравнения касательной и нормали к кривой  в точке в точке  и вычислить и вычислить  . .8. Вычислить производную 2-го порядка от неявной функции:  . .9. Вычислить предел с помощью формулы Тейлора:  . .10. Применима ли теорема Ролля к функции  на отрезке на отрезке 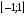 ? ?11. По графику функции построить график ее первой производной 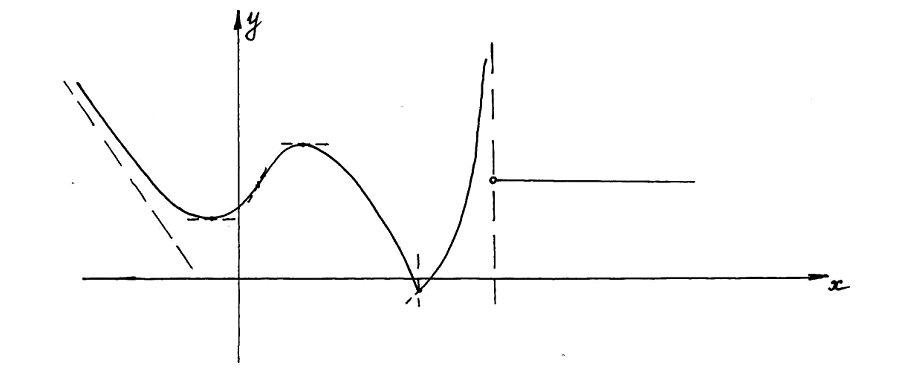 Вариант 4 1. Вычислить пределы с помощью правила Лопиталя: а) 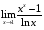 ; б) ; б)  . .2. Провести исследование и построить график функции:  3. Построить график функции в полярной системе координат 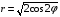 . . 4. Найти радиус основания  и образующую и образующую 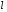 прямого кругового конуса, прямого кругового конуса, вписанного в сферу единичного радиуса и имеющего среди таких конусов наибольший объем. 5. Вычислить  функции функции 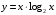 . .6. Используя формулу Тейлора  го порядка, вычислить приближенно го порядка, вычислить приближенно значение 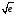 и доказать, что при этом погрешность и доказать, что при этом погрешность  допускает допускает нижеследующую оценку:  . .7. Составить уравнения касательной и нормали к кривой 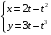 в точке в точке  и вычислить и вычислить  . .8. Вычислить производную 2-го порядка от неявной функции: 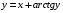 . .9. Вычислить предел с помощью формулы Тейлора:  . .10. Написать формулу Лагранжа для функции  и найти и найти  на на  . .11. По графику функции построить график ее первой производной 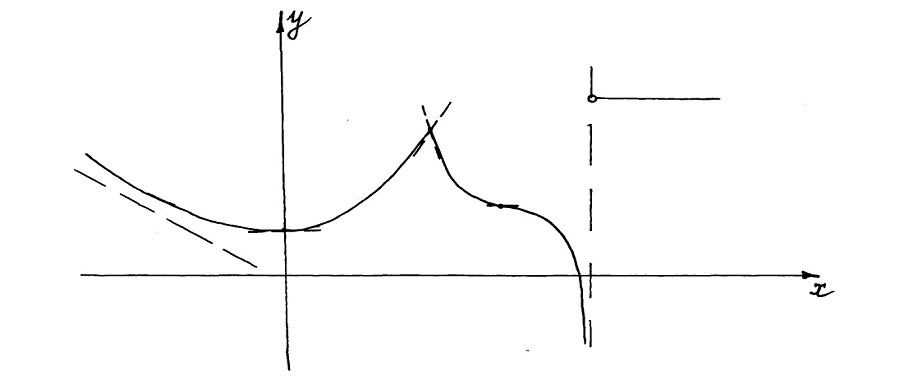 Вариант 5 1. Вычислить пределы с помощью правила Лопиталя: а) 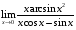 ; б) ; б) 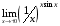 . .2. Провести исследование и построить график функции:  . .3. Построить график функции в полярной системе координат 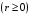  . . 4. На прямой   , найти такую точку , найти такую точку  , чтобы сумма квадратов , чтобы сумма квадратов расстояний от неё до двух прямых: 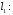  , и , и   , была , была наименьшей. 5. Вычислить 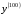 функции функции 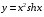 . .6. Используя формулу Тейлора  го порядка, вычислить приближенно значение го порядка, вычислить приближенно значение и доказать, что при этом погрешность и доказать, что при этом погрешность  допускает нижеследующую допускает нижеследующую оценку: 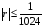 7. Составить уравнения касательной и нормали к кривой  в точке в точке  и вычислить и вычислить  . .8. Вычислить производную 2-го порядка от неявной функции:  . .9. Вычислить предел с помощью формулы Тейлора: 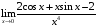 . .10. Написать формулу Коши для функций 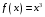 и и 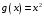 , и найти , и найти  . .11. По графику функции построить график ее первой производной  Вариант 6 1. Вычислить пределы с помощью правила Лопиталя: а) 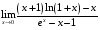 ; б) ; б)  . .2. Провести исследование и построить график функции:  . .3. Построить график функции в полярной системе координат 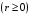 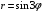 . . 4. Найти стороны 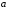 и и 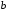 прямоугольника, вписанного в окружность единичного прямоугольника, вписанного в окружность единичного радиуса и имеющего среди всех таких прямоугольников наибольший периметр. 5. Вычислить  функции функции  в точке в точке  . .6. Cчитая, что  и используя формулу Тейлора и используя формулу Тейлора  го порядка, го порядка, вычислить приближенно значение 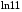 и доказать, что при этом погрешность и доказать, что при этом погрешность  допускает нижеследующую оценку: допускает нижеследующую оценку: 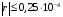 . .7. Составить уравнения касательной и нормали к кривой  в точке в точке  и вычислить и вычислить  . .8. Вычислить производную 2-го порядка от неявной функции:  . .9. Вычислить предел с помощью формулы Тейлора:  . .10. На кривой y = 4 − 6x3, найти точку M(x0, y0), в которой касательная параллельна хорде, соединяющей точки  и и  . .11. По графику функции построить график ее первой производной  Вариант 7 1. Вычислить пределы с помощью правила Лопиталя: а) 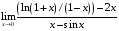 ; б) ; б) 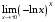 . .2. Провести исследование и построить график функции:  . .3. Построить график функции в полярной системе координат 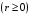  . . 4. Найти сторону основания 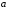 и боковое ребро и боковое ребро 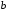 правильной треугольной правильной треугольной призмы, вписанной в сферу единичного радиуса и имеющей среди всех таких призм наибольший объем. 5. Вычислить 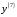 функции функции  . .6. Используя формулу Тейлора  го порядка, вычислить приближенно значение го порядка, вычислить приближенно значениефункции 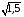 и доказать, что при этом погрешность и доказать, что при этом погрешность  допускает допускает нижеследующую оценку:  . .7. Составить уравнения касательной и нормали к кривой 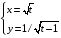 в точке в точке  и вычислить и вычислить  . .8. Вычислить производную 2-го порядка от неявной функции:  . .9. Вычислить предел с помощью формулы Тейлора:  . .10. Написать формулу Лагранжа для функции  и найти и найти  на на  . .11. По графику функции построить график ее первой производной  Вариант 8 1. Вычислить пределы с помощью правила Лопиталя: а)  ; б) ; б)  . .2. Провести исследование и построить график функции: 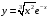 . .3. Построить график функции в полярной системе координат 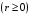 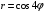 . . 4. Найти верхнее основание трапеции наибольшей площади, вписанной в полукруг радиуса  и имеющей нижним основанием диаметр полукруга. и имеющей нижним основанием диаметр полукруга.5. Вычислить 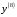 функции функции 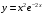 . .6. Вычислить с помощью формулы Тейлора  с точностью до с точностью до 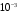 . .7. Составить уравнения касательной и нормали к кривой  в точке в точке 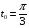 и вычислить и вычислить  . .8. Вычислить производную 2-го порядка от неявной функции:  . .9. Вычислить предел с помощью формулы Тейлора:  . .10. Применима ли теорема Ролля к функции 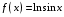 на отрезке на отрезке  ? ?11. По графику функции построить график ее первой производной  Вариант 9 1. Вычислить пределы с помощью правила Лопиталя: а) 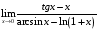 ; б) ; б)  . .2. Провести исследование и построить график функции: 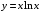 . .3. Построить график функции в полярной системе координат  . . 4. Найти сторону основания 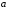 и боковое ребро и боковое ребро 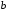 правильной шестиугольной правильной шестиугольной пирамиды, вписанной в сферу единичного радиуса и имеющей среди всех таких пирамид наибольшую боковую поверхность. 5. Вычислить 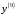 функции функции  . .6. Вычислить с помощью формулы Тейлора 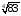 с точностью до с точностью до 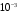 . .7. Составить уравнения касательной и нормали к кривой 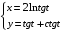 в точке в точке 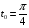 и вычислить и вычислить  . .8. Вычислить производную 2-го порядка от неявной функции:  . .9. Вычислить предел с помощью формулы Тейлора:  . .10. Написать формулу Лагранжа для функции  и найти и найти  на на  . .11. По графику функции построить график ее первой производной  |
