Задания по курсачу матан. Исследование и построить график функции Построить график функции в полярной системе координат
 Скачать 2.8 Mb. Скачать 2.8 Mb.
|
|
Вариант 30 1. Вычислить пределы с помощью правила Лопиталя: а)  ; б) ; б)  . .2. Провести исследование и построить график функции 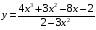 . .3. Построить график функции в полярной системе координат  . . 4. Найти радиус основания  и высоту и высоту  прямого кругового цилиндра, прямого кругового цилиндра, вписанного в сферу единичного радиуса и имеющего среди всех таких цилиндров наибольшую полную поверхность. 5. Вычислить  функции функции  . .6. Оценить с помощью формулы Тейлора абсолютную погрешность приближенной формулы:  , ,  . . 7. Составить уравнения касательной и нормали к кривой  в точке в точке  и вычислить и вычислить  . .8. Вычислить производную 2-го порядка от неявной функции: 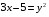 . .9. Вычислить предел с помощью формулы Тейлора:  . .10. Удовлетворяют ли функции  и и  условиям теоремы условиям теоремы Коши на отрезке  ? ? 11. По графику функции построить график ее первой производной  Решение типового варианта по дифференциальному исчислению. 1. Вычислить пределы с помощью правила Лопиталя:   Это есть неопределённость вида  Обозначив выражение под знаком пре- Обозначив выражение под знаком пре-дела через  рассмотрим рассмотрим  Значит,  . .2. Провести исследование и настроить график функции:  Область определения:  функция является нечетной; она непрерывна функция является нечетной; она непрерывна для всех  , поэтому её график вертикальных асимптот не имеет; наклонные и , поэтому её график вертикальных асимптот не имеет; наклонные и горизонтальные асимптоты:  т.е. при  асимптотой является прямая асимптотой является прямая  а при а при  асимптотой является прямая 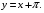 Далее имеем:  знаки знаки   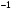  т.е. функция возрастает на интервалах  и и  и убывает на интер- и убывает на интер-вале   является точкой максимума, а является точкой максимума, а  является точкой мини- является точкой мини-мума:  знаки   т.е. график функции будет выпуклым на т.е. график функции будет выпуклым на интервале  , и вогнутым на интервале , и вогнутым на интервале  точка точка 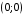 будет точкой будет точкойперегиба графика;  График функции будет иметь вид: График функции будет иметь вид:   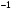   3. Построить график функции в полярной системе координат:  График строится “по точкам” с учетом того, что  возрастает при возрастает при то есть при то есть при  и убывает при и убывает при  то есть при то есть при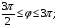    и так далее. В итоге, график будет иметь вид: и так далее. В итоге, график будет иметь вид: 4. Найти радиус основания и высоту конуса наименьшего объема, описан- ного около сферы единичного радиуса.  . .Из подобия треугольников    т.к. т.к.  то отсюда то отсюда   О Теперь     и  где где  Найдем, при каком  эта функция будет наименьшей: эта функция будет наименьшей:  т.к. т.к.  то отсюда то отсюда  Знаки     Значит,  убывает на убывает на  и возрастает на и возрастает на  и функция будет и функция будет наименьшей при  Тогда Тогда   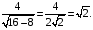 Таким Таким образом,  5. Вычислить 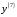 функции функции  . Разделим числитель на знаменатель . Разделим числитель на знаменательи разложим оставшуюся правильную дробь на простые:  при  отсюда отсюда  при при  отсюда отсюда  Таким образом,  Теперь легко найти искомую произ- Теперь легко найти искомую произ-водную:  Теперь вычислим 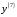 функции функции  . .Используя формулу Лейбница при 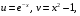 имеем: имеем: (все остальные члены будут равны (все остальные члены будут равны  ); ); 6. Используя формулу Тейлора 2-ого порядка, вычислить приближенно  и идоказать, что при этим погрешность  допускает оценку допускает оценку   Далее используем формулу  в которой    между между 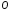 и и 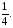 Отбрасывая остаточный член Отбрасывая остаточный член  имеем приближенно имеем приближенно  Погрешность этих вычислений допускает оценку  т.к. т.к.наибольшее значение этой дроби будет при наименьшем её знаменателе, т.е. при  . .7. Составить уравнения касательной и нормали к кривой  в точке  и вычислить и вычислить   Уравнение касательной имеет вид  Уравнение нормали имеет вид  Далее имеет:   . .8. Вычислить производную 2-го порядка от неявной функции: 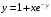 , т.е. , т.е. дифференцируем это равенство по дифференцируем это равенство по  откуда  Дифференцируем это равенство по  еще раз: еще раз:  . .9. Вычислить предел с помощью формулы Тейлора:  Это есть неопределённость вида  Обозначим  тогда наш предел будет равен тогда наш предел будет равен  что в силу 1-ого что в силу 1-ого замечательного предела  приводит к приводит к 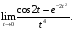 Далее используем готовые Далее используем готовые разложения  и и  подставляя в подставляя в них вместо  соответственно, получим соответственно, получим  Теперь исходный предел будет равен  поскольку последний предел, согласно определению бесконечно малой более высокого порядка, равен  то получаем ответ: то получаем ответ:  10. Написать формулу Лагранжа для функции  и найти и найтисоответствующую точку  Формула Лагранжа имеет вид  для нашей для нашей функции будем иметь  т.е. т.е.  и и  11. По графику функции построить график её первой производной. Под графиком функции будем строить график её производной, учитывая что: - на интервалах возрастания функции  и и  её производная её производная положительна, а на интервале убывания  это производная отрица- это производная отрица-тельна; -точки  и и  являются точками экстремума функции, значит производная являются точками экстремума функции, значит производная функции в этих точках равна  или не существует: или не существует: 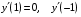 не несуществуют, т.к. в этой график функции имеет вертикальную касательную, а в силу того, что производная – это угловой коэффициент касательной,  - аналогично, т.к. график функции имеет вертикальную касательную и в точке  , то в этой точке производная также имеет бесконечный разрыв; , то в этой точке производная также имеет бесконечный разрыв; - т.к. при  график функции имеет асимптоту (предположительно график функции имеет асимптоту (предположительно ), то график её производной будет иметь горизонтальную асимптоту ), то график её производной будет иметь горизонтальную асимптоту т.е. т.е.   Рис. 1.  Рис. 2. |
