ММТМО. Решение Код import math from decimal import Decimal
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Задание 1 Вариант 13 Условие   Решение 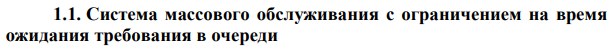 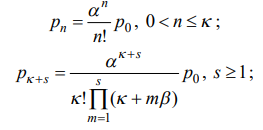 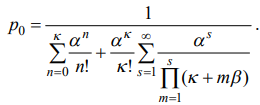 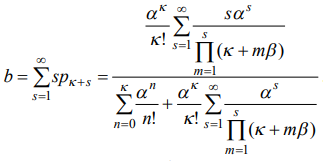 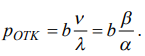 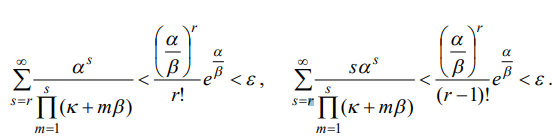 Код import math from decimal import Decimal import matplotlib.pyplot as plt lam = 1.5 mu = 1.2 v = 0.5 k = 1 alpha = lam / mu betta = v / mu eps = .00000001 def get_r(): r = 1 while ((alpha / betta)**r / math.factorial(r-1)) * math.exp(alpha / betta) > eps: r += 1 return r limit = get_r() print('r = ', limit) def calc_on_n(n, alpha): return alpha**n / math.factorial(n) def calc_coef_div(k): return math.factorial(k) def calc_mul_on_s(s, k, betta): mul_on_s = 1 for m in range(1, s + 1): mul_on_s *= k + m*betta return mul_on_s def get_p_0(k, limit, alpha, betta): sum_on_k = 0 for n in range(k + 1): sum_on_k += calc_on_n(n, alpha) coef = alpha**k / calc_coef_div(k) sum_on_lim = Decimal(0) for s in range(1, limit + 1): sum_on_lim += Decimal(Decimal(alpha)**Decimal(s) ) / Decimal(calc_mul_on_s(s, k, betta)) return float(1 / (Decimal(sum_on_k) + Decimal(coef) * sum_on_lim)) def get_p_n(n, k, limit, alpha, betta): return calc_on_n(n, alpha) * get_p_0(k, limit, alpha, betta) def get_b(k, limit, alpha, betta): b = 0 for s in range(1, limit+1): b += s*get_p_ks(s, k, limit, alpha, betta) return b def get_p_otk(k, limit, alpha, betta): return get_b(k, limit, alpha, betta) * betta / alpha def get_p_ks(s, k, limit, alpha, betta): return alpha**(k+s) / (calc_coef_div(k) * calc_mul_on_s(s, k, betta)) * get_p_0(k, limit, alpha, betta) def get_avg_queue(k, limit, alpha, betta): return sum([s * get_p_ks(s, k, limit, alpha, betta) for s in range(1, limit + 1)]) def count_cost(k, limit, alpha, betta): k_cost = 400 product_cost = 1000 total_cost_arr = [] k_arr = [] for temp_k in range(k, k+11): k_arr.append(temp_k) total_cost = get_p_otk(temp_k, limit, alpha, betta) * \ lam * 30 * product_cost + temp_k*k_cost total_cost_arr.append(total_cost) fig, ax = plt.subplots() ax.set_xlabel('Кол-во торговых точек') ax.set_ylabel('Средние суммарные затраты') ax.plot(k_arr, total_cost_arr, marker='o') for i in range(len(k_arr)): ax.annotate( f'({k_arr[i]}; {round(total_cost_arr[i], 3)})', (k_arr[i], total_cost_arr[i])) plt.show() print('Вероятность того, что магазин будет свободен от продажи: ', get_p_0(k, limit, alpha, betta)) print('Вероятность того, что привезенные фрукты не будут своевременно проданы: ', get_p_otk(k, limit, alpha, betta)) print('Среднее количество тонн фруктов, доставленных в магазин и проданных в течение месяца: ', (1 - get_p_otk(k, limit, alpha, betta))*lam*30) print('Среднее количество тонн фруктов, доставленных в магазин в течение месяца и потерянных в результате хранения: ', get_p_otk(k, limit, alpha, betta) * lam * 30) print('Среднее количество тонн фруктов, ожидающих продажи (сутки): ', get_avg_queue(k, limit, alpha, betta)) print('Вероятность хранения фруктов в магазине: ', 1 - sum([get_p_n(n, k, limit, alpha, betta) for n in range(k+1)])) count_cost(k, limit, alpha, betta) Результаты r = 23 Вероятность того, что магазин будет свободен от продажи: 0.20665988311177766 Вероятность того, что привезенные фрукты не будут своевременно проданы: 0.3653279064894208 Среднее количество тонн фруктов, доставленных в магазин и проданных в течение месяца: 28.560244207976062 Среднее количество тонн фруктов, доставленных в магазин в течение месяца и потерянных в результате хранения: 16.439755792023938 Среднее количество тонн фруктов, ожидающих продажи (сутки): 1.0959837194682625 Вероятность хранения фруктов в магазине: 0.5350152629985002 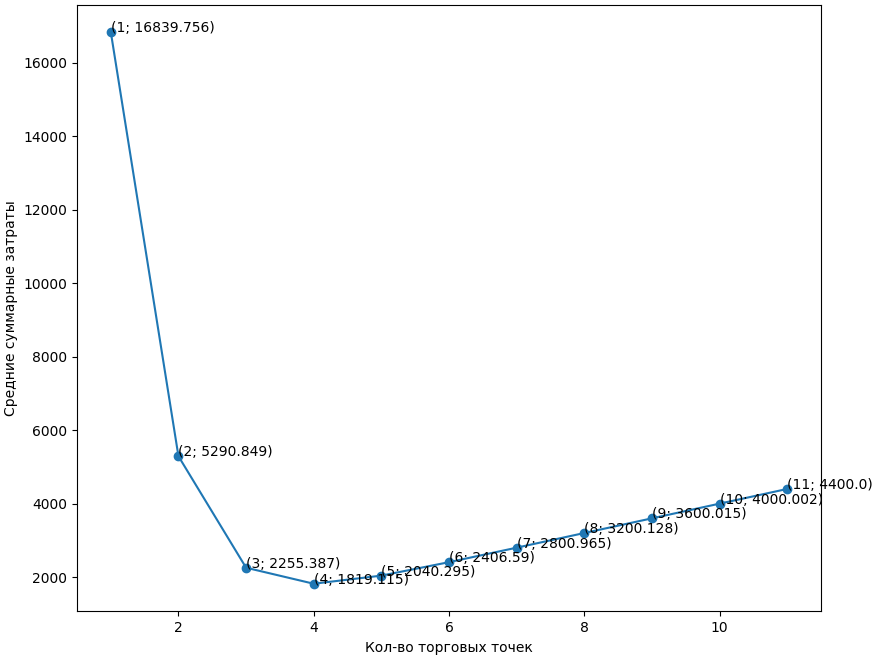 По графику видно, что целесообразно будет открыть ещё три точки: тогда средние суммарные затраты в месяц составят 1819.115 денежных едениц, вместо текущих 16839.756. Задание 2 Вариант 13 Условие   Решение 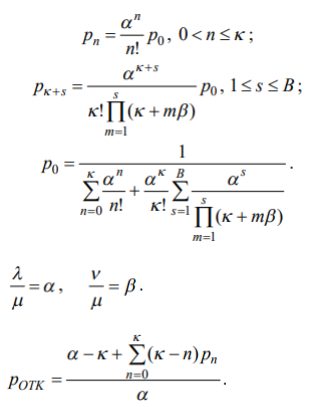 Код import math from decimal import Decimal import matplotlib.pyplot as plt lam = 120 mu = 10 v = 0.1 k = 3 B = 10 alpha = lam / mu betta = v / mu def calc_on_n(n, alpha): return alpha**n / math.factorial(n) def calc_coef_div(k): return math.factorial(k) def calc_mul_on_s(s, k, betta): mul_on_s = 1 for m in range(1, s + 1): mul_on_s *= k + m*betta return mul_on_s def get_p_0(k, B, alpha, betta): sum_on_k = 0 for n in range(k + 1): sum_on_k += calc_on_n(n, alpha) coef = alpha**k / calc_coef_div(k) sum_on_lim = Decimal(0) for s in range(1, B + 1): sum_on_lim += Decimal(Decimal(alpha)**Decimal(s) ) / Decimal(calc_mul_on_s(s, k, betta)) return float(1 / (Decimal(sum_on_k) + Decimal(coef) * sum_on_lim)) def get_p_n(n, k, B, alpha, betta): return calc_on_n(n, alpha) * get_p_0(k, B, alpha, betta) def get_p_otk(k, B, alpha, betta): sum_on_k = 0 for n in range(k+1): sum_on_k += (k-n)*get_p_n(n, k, B, alpha, betta) return (alpha - k + sum_on_k) / alpha def get_p_ks(s, k, B, alpha, betta): return alpha**(k+s) / (calc_coef_div(k) * calc_mul_on_s(s, k, betta)) * get_p_0(k, B, alpha, betta) def get_avg_queue(k, B, alpha, betta): return sum([s * get_p_ks(s, k, B, alpha, betta) for s in range(1, B + 1)]) def get_empl_worker_cnt(k, B, alpha, betta): sum_on_k = 0 for n in range(1, k+1): sum_on_k += n*get_p_n(n, k, B, alpha, betta) sum_on_lim = 0 for s in range(1, B+1): sum_on_lim += get_p_ks(s, k, B, alpha, betta) return sum_on_k + k*sum_on_lim def get_idle_worker_cnt(k, B, alpha, betta): return k - get_empl_worker_cnt(k, B, alpha, betta) print('Вероятность того, что все места для одновременной обработки личного состава заняты', 1 - sum([get_p_n(n, k, B, alpha, betta) for n in range(k)])) print('Вероятность того, что полевой пункт простаивает', get_p_0(k, B, alpha, betta)) print('Среднее число занятых мест для одновременной обработки личного состава', get_empl_worker_cnt(k, B, alpha, betta)) print('Вероятность того, что зараженный человек будет обработан за допустимое время', 1 - get_p_otk(k, B, alpha, betta)) print('Среднее число зараженных человек, которые ожидают обработки в укрытии', get_avg_queue(k, B, alpha, betta)) print('Среднее число зараженных человек, которые находятся в полевом пункте санитарной обработки', alpha * (1 - get_p_otk(k, B, alpha, betta)) + get_avg_queue(k, B, alpha, betta)) prev_p_otk = 1 lam -= (lam/2 + lam*0.1) alpha = lam / mu eps = .03 while (prev_p_otk > 0): k += 1 cur_p_otk = get_p_otk(k, B, alpha, betta) print(f'При {k} местах для обработки, вероятность отказа составит: {cur_p_otk}') prev_p_otk = cur_p_otk Результаты Вероятность того, что все места для одновременной обработки личного состава заняты 0.9999997496703132 Вероятность того, что полевой пункт простаивает 2.9450551382819786e-09 Среднее число занятых мест для одновременной обработки личного состава 2.999999708439541 Вероятность того, что зараженный человек будет обработан за допустимое время 0.24999997570329502 Среднее число зараженных человек, которые ожидают обработки в укрытии 9.65273586306764 Среднее число зараженных человек, которые находятся в полевом пункте санитарной обработки 12.652735571507181 При 4 местах для обработки, вероятность отказа составит: 0.18457449513618585 При 5 местах для обработки, вероятность отказа составит: 0.05913815919442546 При 6 местах для обработки, вероятность отказа составит: 0.013684387349576685 При 7 местах для обработки, вероятность отказа составит: 0.002999034363959282 При 8 местах для обработки, вероятность отказа составит: 0.0007329687623816583 При 9 местах для обработки, вероятность отказа составит: 0.00020514049777653476 При 10 местах для обработки, вероятность отказа составит: 6.271576728185865e-05 При 11 местах для обработки, вероятность отказа составит: 1.9771090493854913e-05 При 12 местах для обработки, вероятность отказа составит: 6.176177453724267e-06 При 13 местах для обработки, вероятность отказа составит: 1.8706310526509877e-06 При 14 местах для обработки, вероятность отказа составит: 5.435848223397007e-07 При 15 местах для обработки, вероятность отказа составит: 1.508684640179799e-07 При 16 местах для обработки, вероятность отказа составит: 3.993451014316918e-08 При 17 местах для обработки, вероятность отказа составит: 1.008204408847746e-08 При 18 местах для обработки, вероятность отказа составит: 2.4297478843730387e-09 При 19 местах для обработки, вероятность отказа составит: 5.596390018069997e-10 При 20 местах для обработки, вероятность отказа составит: 1.233616912325412e-10 При 21 местах для обработки, вероятность отказа составит: 2.6061375280050925e-11 При 22 местах для обработки, вероятность отказа составит: 5.286141894581912e-12 При 23 местах для обработки, вероятность отказа составит: 1.0302869668521453e-12 При 24 местах для обработки, вероятность отказа составит: 1.9095836023552692e-13 При 25 местах для обработки, вероятность отказа составит: 3.4786988104921576e-14 При 26 местах для обработки, вероятность отказа составит: 5.181040781584064e-15 При 27 местах для обработки, вероятность отказа составит: 1.4802973661668755e-15 При 28 местах для обработки, вероятность отказа составит: 0.0 Задание 3 Вариант 13 Условие    Решение   Далее рассмотрим -приборную систему массового обслуживания с ограничением на время пребывания требований в системе. Анализ данной системы сводится к рассмотрению одноприборной системы с ограничением на время пребывания требований в системе, у которой математическое ожидание времени обслуживания определяется зависимостью (2.2). Код import math import mpmath from decimal import Decimal import matplotlib.pyplot as plt k = 6 nu = 1.5/60 lam = 3/60 v = 1/35 mu = 1 / nu mu_ = k * mu nu_ = 1 / mu_ alpha = lam / mu_ betta = v / mu_ k_ = 1 eps = .00000001 def get_r(alpha, betta, eps): r = 1 while ((alpha / betta)**r / math.factorial(r-1)) * math.exp(alpha / betta) > eps: r += 1 return r limit = get_r(alpha, betta, eps) print('r = ', limit) def calc_on_n(n, alpha, betta): return alpha**n / (math.factorial(n) * (1 + betta)**n) def calc_coef_div(k_, betta): return (math.factorial(k_) * (1 + betta)**k_) def calc_mul_on_s(s, k_, betta): mul_on_s = 1 for m in range(1, s + 1): mul_on_s *= k_ + (k_+m)*betta return mul_on_s def get_p_0(k_, alpha, betta, limit): sum_on_k = 0 for n in range(k_ + 1): sum_on_k += calc_on_n(n, alpha, betta) coef = alpha**k_ / calc_coef_div(k_, betta) sum_on_lim = Decimal(0) for s in range(1, limit + 1): sum_on_lim += Decimal(Decimal(alpha)**Decimal(s) ) / Decimal(calc_mul_on_s(s, k_, betta)) return float(1 / (Decimal(sum_on_k) + Decimal(coef) * sum_on_lim)) def get_p_n(k_, n, alpha, betta, limit): return calc_on_n(n, alpha, betta) * get_p_0(k_, alpha, betta, limit) def get_p_ks(s, k_, alpha, betta, limit): return alpha**(k_+s) / (calc_coef_div(k_, betta) * calc_mul_on_s(s, k_, betta)) * get_p_0(k_, alpha, betta, limit) def get_p_otk(k_, alpha, betta, limit): sum_on_k = 0 for n in range(k_+1): sum_on_k += (k_-n)*get_p_n(k_, n, alpha, betta, limit) return (alpha - k_ + sum_on_k) / alpha def get_queue_avg(): sum_on_lim = 0 for s in range(1, limit+1): sum_on_lim += s*get_p_ks(s, k_, alpha, betta, limit) return sum_on_lim print(f'Среднее время обработки отделом одной сводки: {nu_} мин.') print( f'Вероятность того, что сотрудники свободны от работы: {get_p_0(k_, alpha, betta, limit)}') print( f'Вероятность того, что в отделе одна сводка обрабатывается, а сводок, ожидающих обработки, нет: {get_p_ks(0, k_, alpha, betta, limit)}') print( f'Среднее число сводок, ожидающих обработки: {get_queue_avg()}') print( f'Процент своевременно использованной информации: {1 - get_p_otk(k_, alpha, betta, limit)}') print( f'Вероятность того, что информация не будет использована из-за того, что до окончания обработки она уже потеряла свою ценность: {get_p_otk(k_, alpha, betta, limit)}') devices = [] p_otk_arr = [] for i in range(k, k*2+1): devices.append(i) temp_mu_ = i * mu temp_alpha = lam / temp_mu_ temp_betta = v / temp_mu_ p_otk_arr.append((1 - get_p_otk(k_, temp_alpha, temp_betta, limit))*100) plt.xlabel('Число сотрудников') plt.ylabel('Процент своевременно использованной информации') plt.plot(devices, p_otk_arr) plt.show() nu_arr = [] p_otk_arr = [] nu_arr.append(nu) p_otk_arr.append((1 - get_p_otk(k_, alpha, betta, limit))*100) for i in range(10, 51, 5): temp_nu = nu - nu * (i/100) temp_mu = 1 / temp_nu nu_arr.append(temp_nu) temp_mu_ = k * temp_mu temp_nu_ = 1 / temp_mu_ temp_alpha = lam / temp_mu_ temp_betta = v / temp_mu_ p_otk_arr.append((1 - get_p_otk(k_, temp_alpha, temp_betta, limit))*100) fig, ax = plt.subplots() ax.set_xlabel('Длительность обработки сводки данных одним сотрудником') ax.set_ylabel('Процент своевременно использованной информации') ax.plot(nu_arr, p_otk_arr, marker='o') for i in range(len(p_otk_arr)): ax.annotate(f'({nu_arr[i]}; {round(p_otk_arr[i], 3)})', (nu_arr[i], p_otk_arr[i])) plt.show() Результаты r = 17 Среднее время обработки отделом одной сводки: 0.004166666666666667 мин. Вероятность того, что сотрудники свободны от работы: 0.9997916914704674 Вероятность того, что в отделе одна сводка обрабатывается, а сводок, ожидающих обработки, нет: 0.00020826514225369815 Среднее число сводок, ожидающих обработки: 4.33963166099828e-08 Процент своевременно использованной информации: 0.9998809417562029 Вероятность того, что информация не будет использована из-за того, что до окончания обработки она уже потеряла свою ценность: 0.00011905824379709883   Задание 4 Вариант 13 Условие Решение Код Результаты Задание 5 Вариант 13 Условие Решение Код Результаты |
