Векторная алгебра. Тема 3 Векторная алгебра и аналитическая геометрия. Решение Компоненты матрицы с вычисляются следующим образом

• Название: Решение Компоненты матрицы с вычисляются следующим образом
• Анкор: Векторная алгебра
• Дата: 02.06.2022
• Размер: 97.38 Kb.
• Имя файла: Тема 3 Векторная алгебра и аналитическая геометрия.docx
• Тип: Решение; #564362

Тема 3. Векторная алгебра и аналитическая геометрия

№ 1. Найти произведение матриц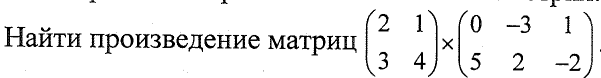



Решение:



Компоненты матрицы С вычисляются следующим образом:

c₁₁ = a₁₁ · b₁₁ + a₁₂ · b₂₁ = 2 · 0 + 1 · 5 = 0 + 5 = 5

c₁₂ = a₁₁ · b₁₂ + a₁₂ · b₂₂ = 2 · (-3) + 1 · 2 = (-6) + 2 = -4

c₁₃ = a₁₁ · b₁₃ + a₁₂ · b₂₃ = 2 · 1 + 1 · (-2) = 2 - 2 = 0

c₂₁ = a₂₁ · b₁₁ + a₂₂ · b₂₁ = 3 · 0 + 4 · 5 = 0 + 20 = 20

c₂₂ = a₂₁ · b₁₂ + a₂₂ · b₂₂ = 3 · (-3) + 4 · 2 = (-9) + 8 = -1

c₂₃ = a₂₁ · b₁₃ + a₂₂ · b₂₃ = 3 · 1 + 4 · (-2) = 3 - 8 = -5

№ 2. Найти угол между векторами



Решение:

Угол между векторами a(X1;Y1;Z1), b(X2;Y2;Z2) можно найти по формуле:

где a * b - скалярное произведение векторов.
Скалярное произведение векторов a и b, заданных своими координатам, находится по формуле: a*b = x1*x2 + y1*y2 + z1*z2.
Найдем скалярное произведение векторов a=(1;1;3) и b(5;-1;2).
По формуле находим:
a*b = 1*5 + 1*(-1) + 3*2 = 10
Найдем модуль вектора a.

Найдем модуль вектора b.

Найдем угол между векторами:

γ = arccos(0.55) = 56.6

№ 3. Дано: А(3,5) и прямая l: 2x-3y+4=0. Написать уравнение прямой, проходящей через точку А и параллельно данной прямой.

Найдем уравнение NK, проходящее через точку А(3;5), параллельно прямой y = 2/3x + 4/3
Уравнение NK параллельно прямой находится по формуле:
y - y₀ = k(x - x₀)
Подставляя x₀ = 3, k = 2/3, y₀ = 5 получим:
y-5 = 2/3(x-3)
или
y = 2/3x + 3 или 3y -2x - 9 = 0

Ответ. 3y -2x - 9 = 0

№4. Написать уравнение плоскости, если А(1,1,1), В(1,0,5), С(2,1,1).

Решение:



Ответ. 4y + z - 5 = 0

№5. Найти точку пересечения прямой и плоскости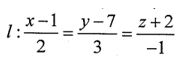



Q: 2х+3у-7z-1=0

Решение.

Представим уравнение (1) в виде двух уравнений:

x − 1 2  =  y − 7 3  ,	(3)
x − 1 2  =  z + 2 −1  .	(4)

Сделаем перекрестное умножение в уравнениях (3) и (4)

3(x−1)=2(y−7)3(x−1)=2(y−7)	(5)
−1(x−1)=2(z−(−2))−1(x−1)=2(z−(−2))	(6)

Откроем скобки и переведем переменные в левую часть уравнений, а остальные элементы в правую часть:

3x−2y=−113x−2y=−11	(7)
−1x−2z=3−1x−2z=3	(8)

Для нахождения точки пересечения прямой l и плоскости Q нужно решить совместно уравнения (2), (7) и (8). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (7) и (8)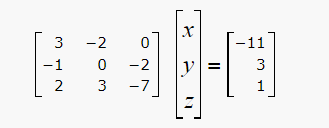



Решим систему линейных уравнений относительно x, y, z:

Запишем решение:

x y z = − 13 5 8 5 − 1 5

(9)

Точка пересечения прямой l и плоскости Q имеет следующие координаты:

M (x, y, z) = M (−13/5, 8/5, −1/5)

Ответ: M (−13/5, 8/5, −1/5).