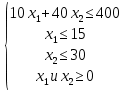ООО «Стройпласт». Решение Математическая модель задачи найти

• Название: Решение Математическая модель задачи найти
• Анкор: ООО «Стройпласт»
• Дата: 16.09.2022
• Размер: 65.36 Kb.
• Имя файла: 1_8618391.docx
• Тип: Документы; #680544

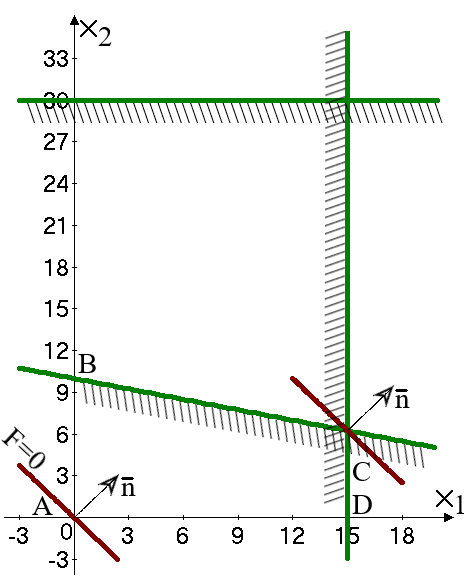
1. Предприятие по производству строительных материалов ООО «Стройпласт» выпускает два вида стройматериалов: жидкое стекло и пенопласт. Трудозатраты на производство 1 т. стекла – 20 человеко-часов, пенопласта – 10 человеко-часов. В кооперативе работают 10 рабочих по 40 ч. в неделю. Оборудование позволяет производить не более 15 т. стекла и 30 т. пенопласта в неделю. Прибыль от реализации 1 т. жидкого стекла 50 тыс. руб.; 1 т. пенопласта – 40 тыс. руб. Сколько стройматериалов каждого вида следует выпускать в неделю для получения максимальной прибыли? а) Записать математическую модель задачи.

б) Решить задачу графическим методом

Решение:

Математическая модель задачи:

найти	Х=(х1;х2)
Для которого	F=50x1+40x2→max
и выполняются ограничения

Построим область допустимых решений задачи, ограниченную неравенствами Штриховкой выделяем нужные полуплоскости, соответствующие знакам неравенств. Областью допустимых решений является фигура ABCD Строим линию уровня целевой функции 5x1+4x2=0 и вектор градиента n = (5, 4) . Двигаем линию уровня параллельно себе по направлению градиента (см. рисунок), пока не выйдем из области.

Видно, что выход из области (максимум целевой функции) произойдет в точке пересечения прямых (I) и (II) , она имеет координаты (15;6.25).

Таким образом, максимум целевой функции F_max=50∙15+40∙6.25=850

Ответ: необходимо производить 15 т стекла и 6.25 т пенопласта. При этом прибыль будет максимальной и составит 850 тыс..

2. Рабочий обслуживает три станка. Вероятность того, что в течение часа станок потребует внимания рабочего, равна для первого станка – 0,3; для второго – 0,3; для третьего – 0,2. Найти: а) вероятность того, что в течение некоторого часа ни один станок не потребует к себе внимания рабочего; б) вероятность того, что, по крайней мере один из трех станков не потребует к себе внимания рабочего в течение часа.

Решение:

Вероятность того, что в течение часа станок потребует внимания рабочего, равна для первого станка – р₁=0,3; для второго – р₂=0,3; для третьего – р₃=0,2. Поэтому вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка – q₁=0,7; для второго – q₂=0,7; для третьего – q₃=0,8.

Вероятность того, что в течение некоторого часа ни один станок не потребует к себе внимания рабочего, определим по теореме умножения вероятностей:

Р₀= q₁∙q₁∙q₁=0,7∙0,7∙0,8=0.392

Событие «хотя бы один не потребует» и «ни один не потребует» образуют полную группу событий, сумма их вероятностей равна единице. Поэтому искомая вероятность равна:

Р₁= 1-Р₀=1-0.392=0.608

Ответ: Р₀=0.392; Р₁= 0.608.

3. В студенческой группе 18 человек, из них 4 юноши, остальные-девушки. Группа разделена наудачу на 2 равные подгруппы. Какова вероятность того, что все юноши попадут в одну подгруппу?

Решение:

Для вычисления вероятности события А (все юноши попали в одну подгруппу) воспользуемся формулой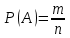

,

где n – общее число возможных элементарных исходов испытания;

m – число элементарных исходов, благоприятствующих появлению события A.

В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно выбрать 9 человек из 18 имеющихся, то есть С₁₈⁹. Общее число благоприятствующих исходов равно числу способов, которыми можно выбрать 5 девушек из 14, и 4 человек из 4 то есть С₁₄⁵∙С₄⁴=С₁₄⁵.

Таким образом,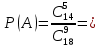





Ответ: Р(А)=0.041.