контрольная работа по математике. 24_решение. Решение методом Крамера
 Скачать 165.96 Kb. Скачать 165.96 Kb.
|
|
Вариант 24 1.Решить систему методом Крамера и методом Гаусса 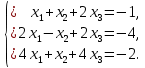 2. Установить совместность системы и найти общее решение. 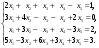 3.Даны координаты вершин треугольника АВС. Найти: 1) уравнения сторон треугольника, представленные в общем виде и с угловым коэффициентом; 2) величину внутреннего угла А, выраженное в градусах; 3) уравнение высоты СН, ее длину; 4) уравнение медианы АМ, ее длину и координаты точки К пересечения этой медианы с высотой СН. А (–5; 9), В (7; 0), С (5; 14). 4.Найти производные первого порядка данных функций. 1) 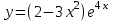 2) 2)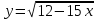 3) 3)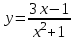 4) 4)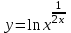 . .5.Составить уравнения касательной и нормали к заданной кривой в точке с абсциссой х0. 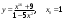 6. Найти пределы 1) 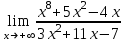 2) 2) 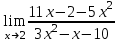 3) 3) 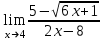 4) 4) 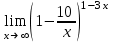 7.Провести полное исследование функции и построить график. 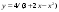 . .1.Решить систему методом Крамера и методом Гаусса 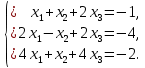 Решение методом Крамера 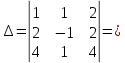 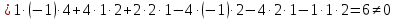 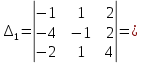 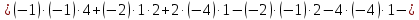 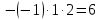 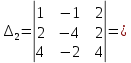 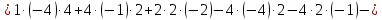 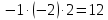 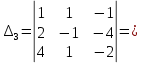 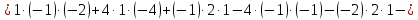 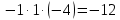 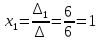 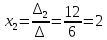 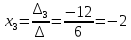 Решение методом Гаусса 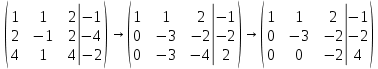 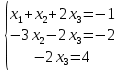 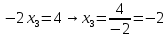 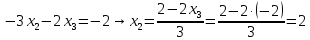 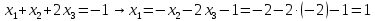 2. Установить совместность системы и найти общее решение. 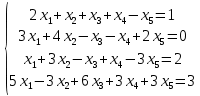 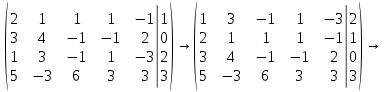 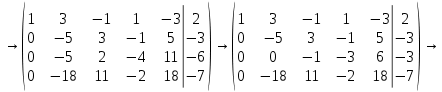 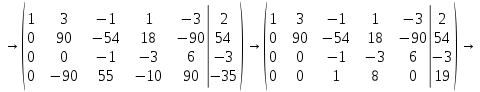 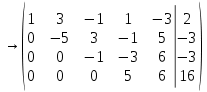  система совместна. система совместна.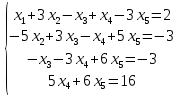 Пусть 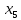 — любое число. — любое число.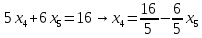 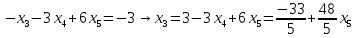 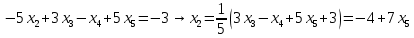 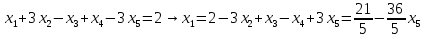 3. Даны координаты вершин треугольника АВС. Найти: 1) уравнения сторон треугольника, представленные в общем виде и с угловым коэффициентом; 2) величину внутреннего угла А, выраженное в градусах; 3) уравнение высоты СН, её длину; 4) уравнение медианы АМ, её длину и координаты точки К пересечения этой медианы с высотой СН. А (–5; 9), В (7; 0), С (5; 14). 1) Направляющий вектор стороны 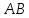 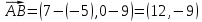 Каноническое уравнение стороны 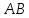 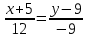 Общее уравнение стороны 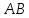 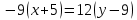 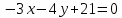 Нормаль к стороне 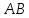 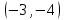 Уравнение стороны 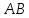 с угловым коэффициентом с угловым коэффициентом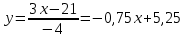 Направляющий вектор стороны 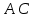 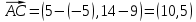 Каноническое уравнение стороны 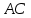  Общее уравнение стороны 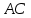 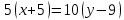 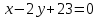 Уравнение стороны 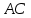 с угловым коэффициентом с угловым коэффициентом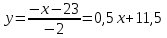 Направляющий вектор стороны 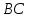 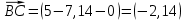 Каноническое уравнение стороны 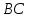 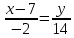 Общее уравнение стороны 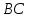 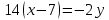 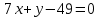 Уравнение стороны 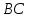 с угловым коэффициентом с угловым коэффициентом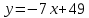 2) Угол 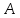 — угол между векторами — угол между векторами 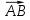 и и 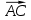 . .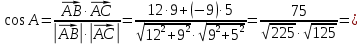 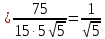 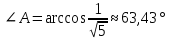 3) Высота 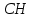 — прямая, проходящая через точку — прямая, проходящая через точку 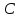 в направлении нормали к стороне в направлении нормали к стороне 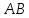 . Каноническое уравнение высоты . Каноническое уравнение высоты 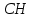 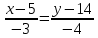 Общее уравнение высоты 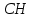 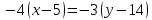 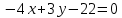 Точка 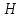 — точка пересечения высоты — точка пересечения высоты 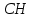 и стороны и стороны 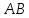 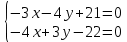 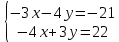 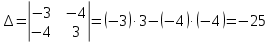 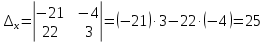 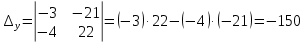 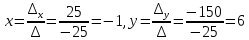 Точка 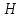 имеет координаты имеет координаты 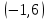 . .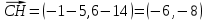 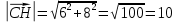 4) Точка 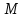 — середина стороны — середина стороны 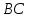 . Координаты точки . Координаты точки 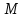 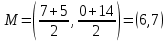 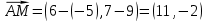 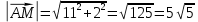 Медиана  — прямая, проходящая через точку — прямая, проходящая через точку  в направлении вектора в направлении вектора 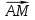 . Каноническое уравнение медианы . Каноническое уравнение медианы 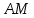 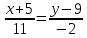 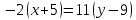 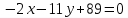 Точка 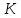 — точка пересечения высоты — точка пересечения высоты 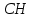 и медианы и медианы 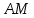 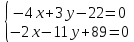 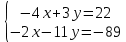 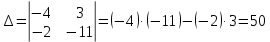 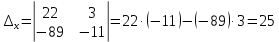 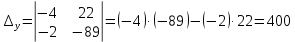 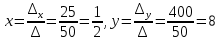 Точка  имеет координаты имеет координаты 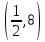 . .4. Найти производные первого порядка данных функций. 1) 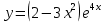 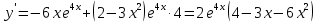 2) 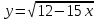 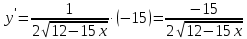 3) 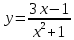 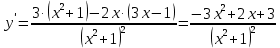 4) 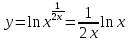 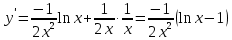 5. Составить уравнения касательной и нормали к заданной кривой в точке с абсциссой 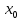 . .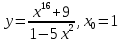 Уравнение касательной 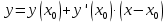 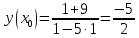 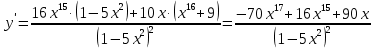 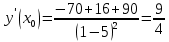 Тогда уравнение касательной 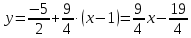 Уравнение нормали 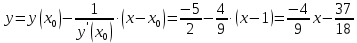 6. Найти пределы 1) 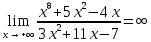 , так как степень числителя больше степени знаменателя , так как степень числителя больше степени знаменателя2) 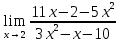 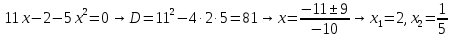 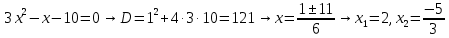 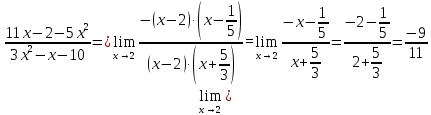 3) 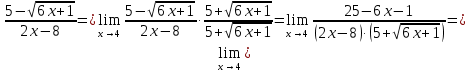 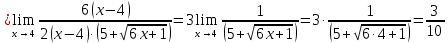 4) 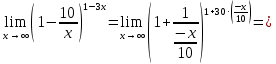 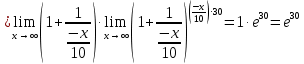 7. Провести полное исследование функции и построить график. 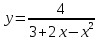 Область определения функции 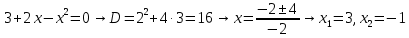 Таким образом, область определения функции 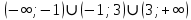 Исследуем поведение функции в окрестности точек разрыва 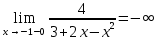 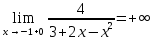 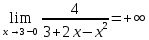 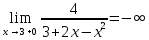 Таким образом, точки 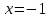 и и 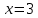 — разрывы второго рода. — разрывы второго рода.Функция не чётная, ни нечётная 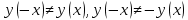 Функция непериодическая. Точки пересечения с осями координат 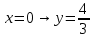 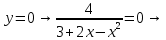 решений нет, график функции не пересекает ось решений нет, график функции не пересекает ось  . .Асимптоты функции Точки 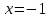 и и 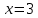 — разрывы второго рода, следовательно — разрывы второго рода, следовательно 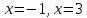 — вертикальные асимптоты. — вертикальные асимптоты.Наклонные асимптоты: 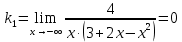 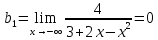 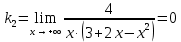 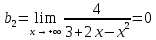  — горизонтальная асимптота. — горизонтальная асимптота.Стационарные точки 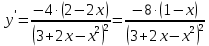 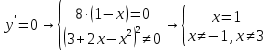 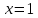 — стационарная точка; — стационарная точка; 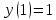 . .Интервалы монотонности функции: 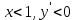 ; ; 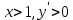 Функция убывает на 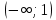 , функция возрастает на , функция возрастает на 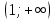 . .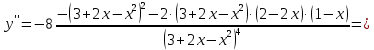 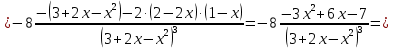 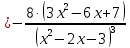 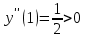 Точка 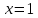 : : 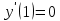 , , 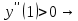 точка точка 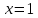 — локальный минимум. — локальный минимум.Точки перегиба 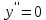 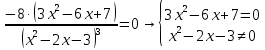 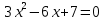 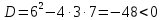 Точек перегиба нет. Интервалы выпуклости функции 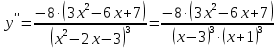 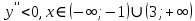 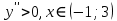 Функция выпукла вверх на 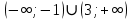 . .Функция выпукла вниз на 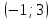 . .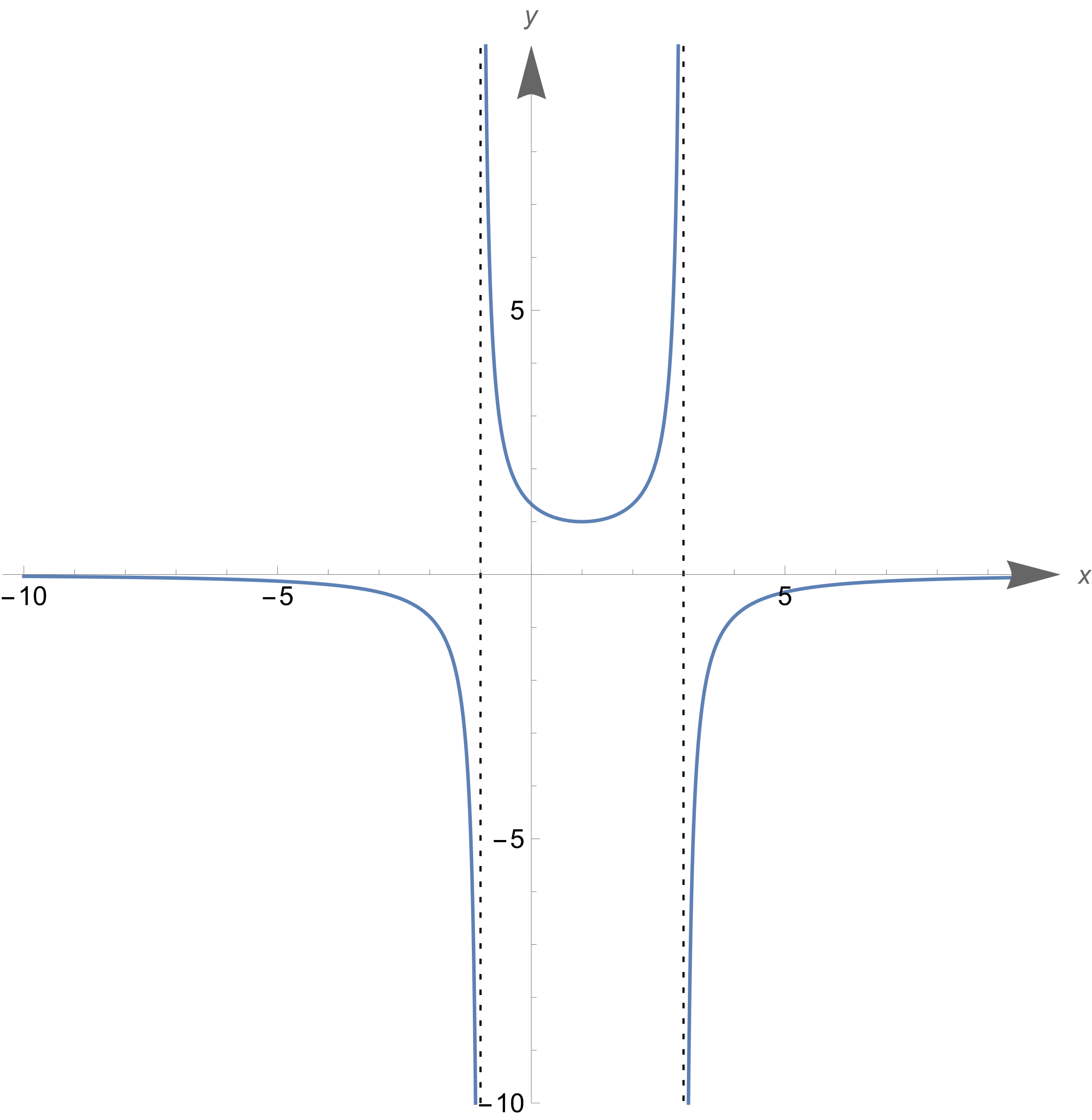 |
