Возбуждение плоского регулярного волновода, решение методом отражений. реф. Решение методом отражений a b a x
 Скачать 107 Kb.
|
|
Возбуждение плоского регулярного волновода, решение методом отражений      a b    a      x y Волноведущую систему (волновод) называют регулярной, если ее параметры (свойства среды и геометрия поперечного сечения) не зависят от одной из координат, которая принимается за ось z цилиндрической системы координат. Следовательно, речь идет о бесконечных металлических трубах постоянного поперечного сечения, заполненных однородной изотропной средой. Из всех типов таких устройств мы рассмотрим простейшие, с поперечным сечением,   z z допускающим разделение переменных в скалярном волновом уравнении, записанном в декартовых или цилиндрических координатах. Таковыми являются, в частности, прямоугольные и круглые регулярные волноводы. Вначале рассмотрим случай прямоугольного волновода. Предположим, что поле в волноводе возбуждается электрическим диполем единичной амплитуды, с моментом, параллельным оси z. Известно, что такой диполь возбуждает электромагнитное поле, имеющее единственную компоненту электрического поля Ez , и поперечное магнитное поле с компонентами Hx , Hy. Тогда, скалярный потенциал Боргниса U(x , y , z ; x0 , y0 , z0) ,черезкоторыйвыражаются все компоненты электромагнитного поля (лекция 2),должен быть решением следующей краевой задачи первого рода: U +  U = ( x x0)( y y0)( z z0); 0 x a; 0 y b; - z ;U| y = 0; y = b = U| x = 0; x = a = 0. (1.16.1) Предполагается также, что U удовлетворяет условию отсутствия волн, приходящих из бесконечности, в виде принципа предельного поглощения. Очевидно, что собственными функциями поперечного сечения, удовлетворяющими нулевым краевым условиям на сторонах прямоугольника, являются Un, m(x,y) =   . (1.16.2)При этом, нормировочный коэффициент, превращающий Un, m(x,y) в полную систему ортонормированных в прямоугольнике функций, равен  . Коэффициенты  разложения   полного решения задачи (1.16.1) по этой системе функций очевидно должны удовлетворять О. Д. У.  + (k2 ( )2 ( )2 )  = ( z z0),решением которого, - функцией Грина одномерной задачи на интервале - z , удовлетворяющей условиям отсутствия волн, приходящих из бесконечности, является 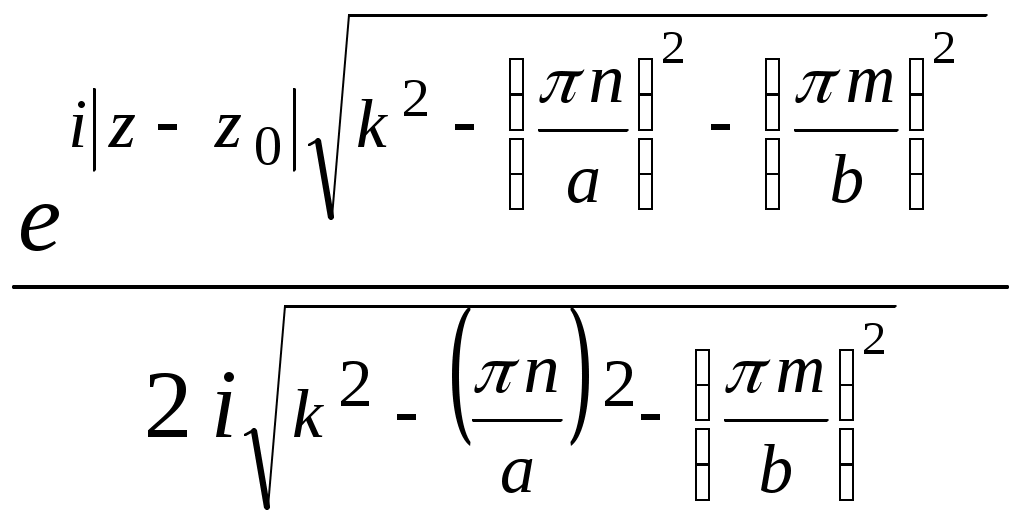=  . (1.16.3)Следовательно, полное решение задачи (1.16.1) выписывается через (1.16.2), (1.16.3), с учетом нормировки, в виде U(x , y, z ;x0 , y0 , z0) = 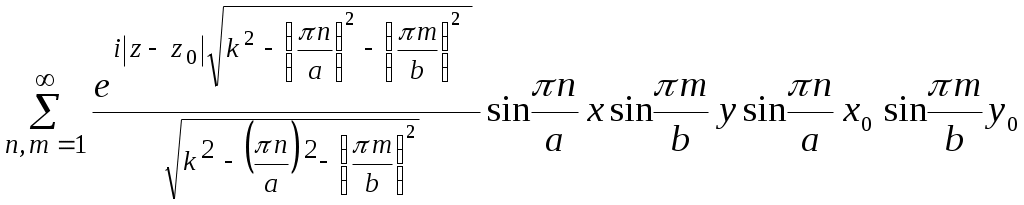  . (1.16.4)Как и в случае плоского волновода, распространяющимся является лишь конечный набор Е – поляризованных волн, для которых 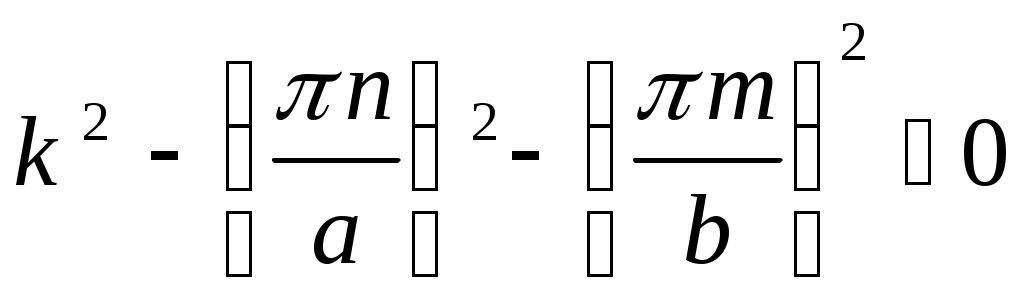 . В соответствии с зависимостью от пары индексов n и m , они обозначаются через Е1, 1, Е1, 2, Е 2, 1 , Е2, 2 , и т. д.Замечание . В случае Н – поляризованного поля в прямоугольном волноводе, когда оно возбуждается полем горизонтального магнитного диполя, краевая задача для потенциала U(x , y , z ; x0 , y0 , z0) становится задачей с краевым условием второго рода: 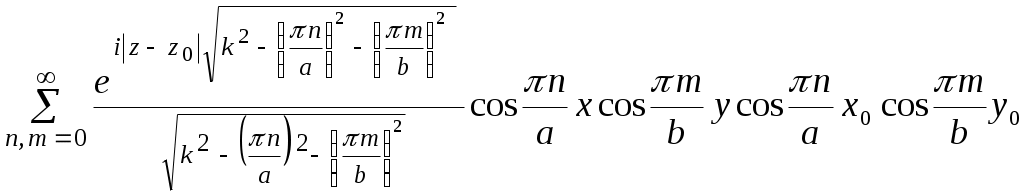 | y = 0; y = b=  | x = 0; x = a= 0. В этом случае собственными функциями поперечного сечения являютсяUn, m(x,y) =   , а решение такой краевой задачи имеет вид  .В соответствии с двойной индексацией, распространяющиеся волны обозначаются в этом случае через Н0, m, Нn, 0, Н n, m. Несмотря на то, что суммирование по n и m начинается с 0 , слагаемому с U0, 0 (x,y) соответствует тривиальное электромагнитное поле с нулевыми компонентами (см. лекцию 2). Обратимся теперь к случаю круглого волновода с идеально проводящей границей. Постановка краевой задачи для функции Боргнися U(r , , z ; r0 , 0 , z0) электрического типа, когда поле возбуждается горизонтальным электрическим диполем, имеет вид U + U =  ( r r0)( 0)( z z0); 0 r a; 0 2 ; - z ; Ur = a = 0, (1.16.5)с условием отсутствия волн, приходящих из бесконечности в прежней форме. Нормированными собственными функциями поперечного сечения являются на этот раз уже рассмотренные нами (лекция 7) функции Un, m(r, ) = 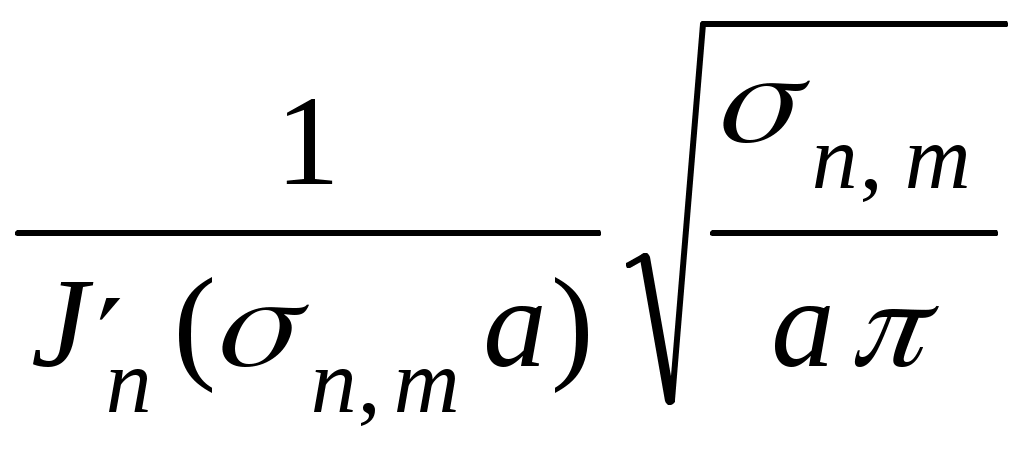   , (1.16.6)где  =  , а - корни уравнения  = 0.Если искать решение краевой задачи (1.16.5) в виде ряда U(r , , z ; r0 , 0 , z0) =  , (1.16.7)то коэффициенты должны быть функциями Грина для О.Д.У. + (k2 ( )2 ) = ( z z0),с условиями отсутствия волн, приходящих из бесконечности. Явный вид этих функций аналогичен (1.16.3): 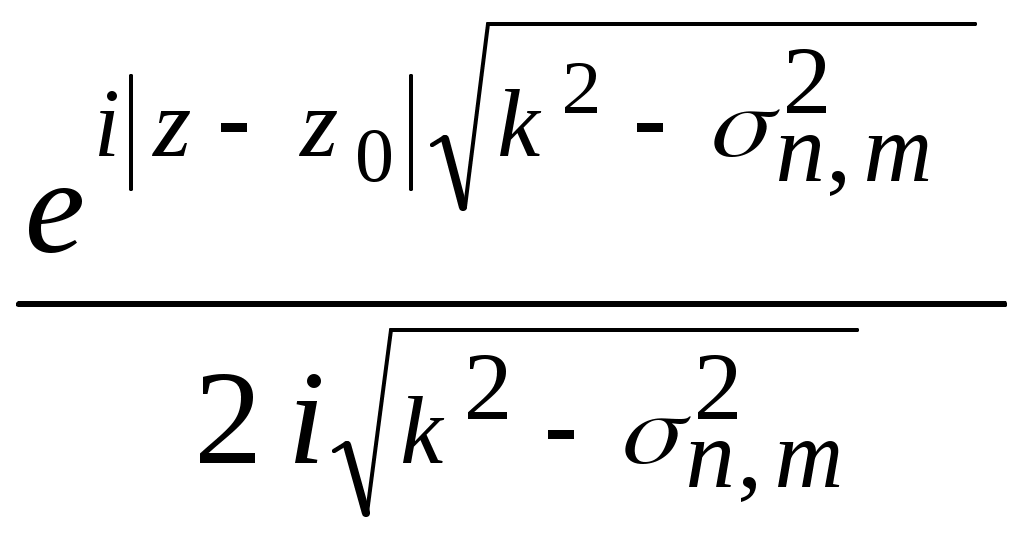=  . (1.16.8)Подставляя (1.16.8) и (1.16.6) в (1.16.7), получим 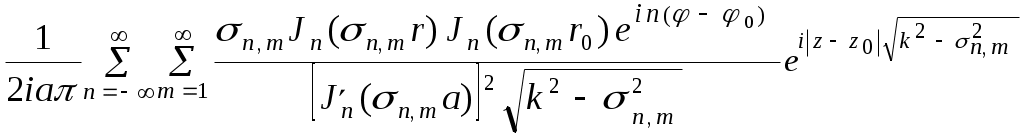 . (1.16.9)Так как  образуют монотонно возрастающую по n и m последовательность положительных чисел, то в круглом волноводе также может распространяться лишь конечный набор волн, для которых  . В соответствии с зависимостью от пары индексов n и m , они обозначаются через Еn, m.В случае задачи возбуждения круглого волновода полем горизонтального магнитного диполя, краевое условие на границе поперечного сечения заменяется наU/rr = a = 0. Полная система собственных функций поперечного сечения, удовлетворяющая этому краевому условию, строится при этом так, как описано в лекции 7 для случая краевой задачи второго рода в круге. |