компьютерное моделирование. 1 лекция. Решение на них задач производится с целью получения неизвестных ранее данных, предсказания новых свойств и будущих поведений, извлечения пользы при реализации решений

• Название: Решение на них задач производится с целью получения неизвестных ранее данных, предсказания новых свойств и будущих поведений, извлечения пользы при реализации решений
• Анкор: компьютерное моделирование
• Дата: 13.09.2020
• Размер: 169.35 Kb.
• Имя файла: 1 лекция.docx
• Тип: Решение; #137748
• страница: 2 из 2

Аналитический способ представления задачи 1

Аналитический явный способ

Эта модель весьма далека от реальности. Что-либо изучить на ней представляется проблематичным, так как из неё можно найти только время T и место встречи S. Идеализация заключается в том, что дорога считается идеально прямой, без уклонов и подъёмов, скорости объектов считаются постоянными, желания объектов не меняются, силы безграничны, отсутствуют помехи для движения, модель не зависит от величин D, V₁, V₂ (они могут быть сколь угодно большими или малыми).

Ь

T1 := D/(V1 + V2) S1 := V1 · T1

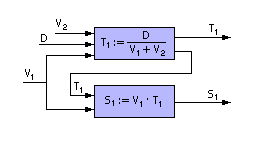
Реальность обычно не имеет ничего общего с такой постановкой задачи. Но за счёт большой идеализации (идеализации большого порядка) получается очень простая модель, которая может быть разрешена в общем виде (аналитически) математическими способами. Так формулируются чаще всего алгоритмические модели, где протянута цепочка вычислений от исходных данных к выходу. Поэтому мы применили в записи знак присваивания (:=). После вычисления правой части выражения её значение присваивается переменной, стоящей в левой части. Далее значение этой переменной применено в правой части следующего выражения. Схематически это выглядит так, как показано на рис. 1.18.

Рис. 1.18. Схема решения задачи о встрече (аналитический явный способ)

Аналитический неявный способ

В данной формулировке за счёт использования знака уравнивания получена связь переменных f(T, V₁, V₂, D, S) = 0 в виде системы уравнений. Устанавливая знак «?» на различные переменные, можно формулировать при необходимости целый ряд произвольных задач, например так:

T1 · (V1 + V2) = D S1 = V1 · T1 T1 = ?

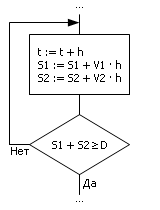
При этом задачи формулируются пользователем и не предусматриваются специально моделировщиком. То есть модель имеет вид объекта. Мы получили более качественную модель. Идеализация её велика, но за счёт неявной формы записи появилась возможность изменения задачи, изучения на ней целого ряда проблем.

Имитационный способ представления задачи 1

При имитационном способе решения обязательным является наличие некоего счётчика, который позволяет моделировать процесс по шагам или по деталям процесса.

Имитационный алгоритмический способ

Повторяя пошагово расчёт в цикле, на каждом этапе работы алгоритма будем имитировать течение процесса (рис. 1.19). Обратите внимание, что процесс берётся не в целом, а как бы в деталях, по шагам. Переменная t является координатой, а значит, отслеживается счётчиком с шагом h. Идея имитации — продвигать пешехода и велосипедиста на величину V · h на каждом такте, где h — достаточно малая величина. Поскольку мы рассматриваем множество актов движения по отдельности, можно по ходу менять все переменные модели, например, V. Если путь пройден большой (S₁), то можно устроить привал (V = 0) на некоторое время. Остановка процесса имитации определяется суммой путей, пройденных велосипедистом и пешеходом навстречу друг другу, и сравнением её с расстоянием D.

Рис. 1.19. Блок-схема решения задачи о встрече (имитационный алгоритмический способ)

На формально-математическом языке алгоритм выглядит так, как показано ниже.

t := t + h · e S1 := S1 + V1 · h · e S2 := S2 + V2 · h · e e := ed(D – (S1 + S2)) f := not(e) stop(f)

e — вспомогательный флаг; f — флаг, показывающий, был ли пройден к текущему моменту t весь путь или нет; ed(x) — единичная функция: ed(x) = 1 при x ≥ 0, иначе ed(x) = 0; stop(z) — функция останова вычислений при z > 0.

Этот способ — ещё один шаг к усложнению модели и приближению её к реальным условиям. Если во всех предыдущих случаях скорость V была известна, то теперь она — непредсказуема, даже статистически, что чаще всего и наблюдается в реальных условиях. Скорость V объекта принимается из некоторых дополнительных моделей. Причём эти модели могут быть с обратными связями. Например, скорость может зависеть от обстановки, степени достижения цели, плана, целесообразности поведения, знания местности, желания двигаться (психологический мотив). Такая постановка ведёт к адаптивным системам и системам искусственного интеллекта.

Например, если объект (пешеход) имеет возможность осмотреть местность с обзорной башни, то он может заранее просчитать свой путь и затем следовать ему. Без обзорной башни пешеход может зайти в безвыходный тупик или бесконечно долго перебирать варианты пути. Для адаптивных систем вводится критерий для оценки перспективности выбора направления движения.

Итак, подведём итог.

Модель — способ замещения реального объекта, используемый для его исследования, когда натуральный эксперимент невозможен, дорог, опасен, долговременен.

Примеры. Поскольку исследование Луны небезопасно для человека, для этой цели используют луноход как модель исследователя; поскольку реальные эксперименты над экономикой страны дороги по своим последствиям, то используют математические модели экономики для изучения последствий управляющих решений; поскольку процесс обработки металлов взрывом скоротечен во времени, то его изучают на модели в увеличенном масштабе времени, а процесс коррозии — в уменьшенном; атом изучается в увеличенном масштабе пространства, а космогонические процессы — в уменьшенном масштабе пространства; поскольку при проектировании объекта его попросту не существует, то исследование будущих свойств объекта ведётся на модели.

Модель несёт системообразующую и смыслообразующую роль в научном познании. На модели изучают неизвестные свойства предметов. Модель стремится как можно более ярко выразить структуру явления, его главные аспекты. Модель является концентрированным выражением сущности предмета или процесса, выделяя только его основные черты.

Знания — это модели окружающего мира, фиксируемые человеком в его мозгу или на технических носителях. Модели обладают повышенной наглядностью, выделяя главные аспекты сущности, и активно используются в процессах познания и обучения. Человек, решая, как ему поступить в той или иной ситуации, всегда пытается представить себе последствия решения, для этого он проигрывает ситуацию, представляет её себе мысленно, строя модель в голове. Компьютер является усилителем для производства данной деятельности, инструментом информационной технологии. Компьютерные модели ускоряют процесс исследования, делают его более точным.

Алгоритмы — знания, выстраиваемые человеком (или, шире, разумным существом) в цепочку так, чтобы соединить исходное состояние с желаемым, целью; это один из вариантов ряда мероприятий, шагов, приводящих к цели.

Таким образом, модели — это основа разумной мыслительной деятельности; модели играют роль базиса, а моделирование — роль инструмента для прогнозирования.

Процесс моделирования состоит из трёх стадий: формализации (переход от реального объекта к модели), моделирования (исследование и преобразования модели), интерпретации (перевод результатов моделирования в область реальности).

Модель есть зависимость F между входом X и выходом Y. Модель отражает закономерность Y = F(X). Часто модель является законом. Модель верна в рамках допущенных при её построении гипотез. Поэтому модель ограничена некоторой областью и адекватна в ней.

Набор моделей образует научную дисциплину (механика, физика, горное дело и т. д.) Модель может быть расширена путём учёта в ней дополнительных параметров. Тогда область её применения становится шире.

Объект может быть представлен в виде аналитической или имитационной модели. Л

Аналитическое представление подходит лишь для очень простых и сильно идеализированных задач и объектов, которые, как правило, имеют мало общего с реальной (сложной) действительностью, но обладают высокой общностью. Аналитические модели обычно применяют для описания фундаментальных свойств объектов (поэтому ими так широко пользуется теоретическая физика), так как фундамент прост по своей сути. Сложные объекты редко удаётся описать аналитически.

Имитационное моделирование позволяет разлагать большую модель на части (объекты, «кусочки»), которыми можно оперировать по отдельности, создавая другие, более простые или, наоборот, более сложные модели. Таким образом, имитационное моделирование тяготеет к объектно-ориентированному представлению, которое естественным образом описывает объекты, их состояние, поведение, а также взаимодействие между ними. Имитационную модель можно постепенно усложнять и усложнять; аналитический способ этого не допускает или допускает, но с большими ограничениями.

Модель может быть соединена с другими моделями. Математически это означает совместное решение моделей (пересечение) и наложение тождеств на связываемые переменные. При связывании модели образуют систему, которая имеет определённую структуру (вложенную, параллельную, последовательную, смешанную, с обратными связями и т. д.)

Если к построенной модели добавить вопрос, то с помощью неё можно решить задачу, получить ответ, который заранее не очевиден. Если ответ заранее очевиден, то модель не строят. Обычно одна и та же модель годится для решения множества задач. Решая задачи, человек обычно строит модели в своей голове и оживляет (интерпретирует) их там же или на искусственном носителе (в среде моделирования).

Повторим:

модель + вопрос + дополнительные условия = задача.

В виде условий могут быть любые дополнительные выражения: равенства, присваивания начальных данных, неравенства, цели, функционалы и т. д., имеющие смысл ограничений, условий, дополнительных связей.

В виде вопроса может служить одна (или несколько) из неизвестных переменных.

Задача доопределяет свободные переменные модели, сужает область возможных решений.

Задачи, решаемые на модели, делятся на прямые и обратные. Прямые задачи по заданному X находят Y путём подстановки X в уравнение Y = F(X). Обычно такие задачи называют задачами анализа. Обратные задачи по заданному Y находят X путём нахождения обратной функции F^–1 и подстановки X = F^–1(Y). Обычно их называют задачами синтеза. Если найти обратную функцию F^–1 в явном виде затруднительно, то составляют вычислительные схемы для численного определения X. Часто к этому виду приводятся задачи управления объектами.

Ещё одной специфической задачей является нахождение по заданным X и Y зависимости F или её коэффициентов. Это задача построения (или настройки) модели.

Роль модели

Построив модель, исследователь может:

• 
  прогнозировать свойства и поведение объекта как внутри области, в которой построена модель, так и (при обоснованном применении) за её пределами (прогнозирующая роль модели);
  
• 
  управлять объектом, отбирая наилучшие воздействия путём испытания их на модели (управляющая роль);
  
• 
  познавать явление или объект, модель которого он построил (познавательная роль модели);
  
• 
  получать навыки по управлению объектом путём использования модели как тренажёра или игры (обучающая роль);
  
• 
  улучшать объект, изменяя модель и испытывая её (проектная роль).
  

Адекватность модели

Поскольку модель является выражением конечного ряда и только важнейших для конкретного исследования аспектов сущности, то она не может быть абсолютно идентичной моделируемому объекту. Кроме этого, реальный объект бесконечен для познания. Поэтому нет смысла стремиться к бесконечной точности при построении модели. Для выяснения необходимой степени адекватности обычно строят ряд моделей, начиная с грубых, простых моделей и двигаясь ко все более сложным и точным. Как только затраты на построение очередной модели начинают превышать планируемую отдачу от модели, то уточнение модели прекращают. Первоначальные шаги производятся в каком-либо существующем универсальном моделирующем пакете. После одобрения модели под неё пишется специализированный пакет. Необходимость в этом возникает в случае, если функционирование модели в универсальной среде моделирования не удовлетворяет требованиям быстродействия (или каким-то другим).

В задачи данного курса входит изучение приёмов и способов, необходимых для формализации, изучения и интерпретации систем.

Моделирование — прикладная инженерная наука класса технологических. Моделирование — дисциплина, ставящая целью построение моделей и их исследование посредством собственных универсальных методов, а также специфических методов смежных с ней наук (математика, исследование операций, программирование).