Практическая работа. Правоведение. Практические задания. Правоведение.. Решение Найдем вероятность выбора первой букв Р Количество событий общему количеству букв 6
 Скачать 29.42 Kb. Скачать 29.42 Kb.
|
Москва 2021 Практические задания Задание 1. Буквы, составляющие слово РАКЕТА, написаны по одной на шести карточках, карточки перемешаны и положены в пакет. Чему равна вероятность того, что, вынимая четыре буквы, получим слово РЕКА. Решение: Найдем вероятность выбора первой букв Р: Количество событий = общему количеству букв = 6 Из них благоприятных событий (подходящих букв) = 1 Вероятность по формуле Лапласа: Р = 1/6. Вероятность, что вторая буква Е: Р = 1/5 (из оставшихся 5-ти букв 1 Е); Вероятность того, что третья буква будет К: Р = 1/4 (из оставшихся 4-х букв 1 К); Вероятность того, что четвертая буква будет А: Р = 2/3 (из оставшихся 3-х букв 2А); Вероятность взаимосвязанных событий, что поочередно вынуты буквы Р, Е, К, А: Р = (1 / 6) * (1 / 5) * (1 / 4) * (2 / 3) = 1/180. Ответ: Вероятность того, что, вынимая шесть букв получим слово РЕКА составляет 1/180. Какова вероятность сложить слово КАРЕТА при вынимании всех букв? Решение: Найдем вероятность выбора первой буквы К: Количество событий = общему количеству букв = 6. Из них благоприятных событий (подходящих букв) = 1. Вероятность по формуле Лапласа: К = 1 / 6. Вероятность, что вторая буква А: Р = 2/5 (из оставшихся 5-ти букв 2 А); Вероятность того, что третья буква будет Р: Р = 1/4 (из оставшихся 4-х букв 1 Р); Вероятность того, что четвертая буква будет Е: Р = 1/3(из оставшихся 3-х букв 1 Е); Вероятность того, что пятая буква будет Т: Р = 1/2 (из оставшихся 2-х букв 1 Т); Вероятность того, что шестая буква будет А: Р = 1/1(из оставшейся 1-й буквы 1 А); Вероятность взаимосвязанных событий, что поочередно вынуты буквы К, А, Р, Е, Т, А: Р = (1 / 6) * (2 / 5) * (1 / 4) * (1 / 3) * (1/2) * (1/1) = 1/360. Ответ: Вероятность того, что, при вынимании всех букв буквы, получим слово КАРЕТА равна 1/360. Задание 2. Дискретная случайная величина ξ задана следующим законом распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение. Дискретная случайная величина ξ задана следующим законом распределения: Решение: Математическое ожидание находим по формуле m = ∑ξipi. Математическое ожидание M[ξ]. M[ξ] = 4*0,4+6*0,1+10*0,2+12*0,3=7,8 Дисперсию находим по формуле d = ∑ξ2ipi - M[ξ]2. Дисперсия D[ξ]. D[ξ] = 42*0,4 + 62*0,1 + 102*0,2 + 122*0,3 – 7,82 = 73,2 – 60,84 = 12,4 Среднее квадратическое отклонение σ(ξ). σ(ξ) = √ D| ξ | =√12,4 = 3,5. Задание 3. Возможные значения дискретной случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание M[ξ] = 1.9, а также M[ξ]2= 7.3, найти вероятности р1, р2, p3 которые соответствуют дискретным значениям случайной величины. Дисперсия случайной величины ξ: Dξ= M ξ2 – (M ξ)2 = 7,3 – 1,92 = 7,3 –3,61 = 3,69, Поскольку ξ дискретная, то 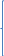 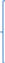 Mξ = Mξ = 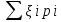 = (-2)* = (-2)* 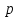 1 + 1* 1 + 1* 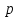 2 + 4* 2 + 4* 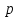 3 =1,9 3 =1,9Dξ= 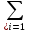 ξ2 ξ2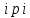 = (-2)2 * = (-2)2 * 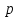 1 + 12 * 1 + 12 * 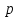 2 + 42 * 2 + 42 * 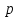 3 = 4 3 = 4 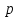 1 + 1 + 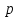 2 + 16 2 + 16 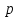 3 = 3,69 3 = 3,69Учитываем условие, что 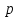 1 + 1 + 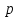 2 + 2 + 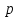 3 = 1. 3 = 1.Решаем как систему уравнений: 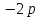 1 + 1 + 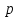 2 + 4 2 + 4 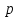 3 =1,9 p1 = 3 =1,9 p1 = 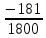 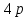 1 + 1 + 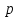 2 + 16 2 + 16 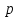 3 =3,69 → p2 = 3 =3,69 → p2 =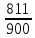 ; ;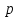 1 + 1 + 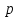 2 + 2 + 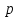 3 =1 p3 = 3 =1 p3 = 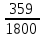 Значение вероятности p1 < ¿ 0, что неверно, поэтому задача не имеет решения. Ответ: Так как значение вероятности p1 < ¿ 0, задача не имеет решения. |
