Задача 2. Задача 2 (1). Решение нелинейного уравнения
 Скачать 26.55 Kb. Скачать 26.55 Kb.
|
|
Задача 2 2.1 Решение нелинейного уравнения 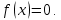 Пользователь вводит отрезок, точность для значения корня. Можно предусмотреть ввод функции 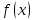 . Тестирование провести для функции по варианту. При разработке алгоритма учесть возможные варианты – корни на введенном промежутке отсутствуют, корень один, корней несколько, корней бесконечное множество. Для поиска отдельного корня с указанной точностью использовать численные методы. Для наглядности можно включить построение графика функции . Тестирование провести для функции по варианту. При разработке алгоритма учесть возможные варианты – корни на введенном промежутке отсутствуют, корень один, корней несколько, корней бесконечное множество. Для поиска отдельного корня с указанной точностью использовать численные методы. Для наглядности можно включить построение графика функции 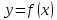 с выделением решений в графическом способе. с выделением решений в графическом способе.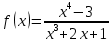 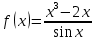 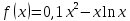 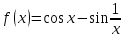 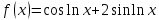 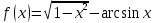 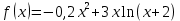 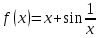 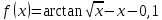 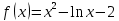 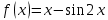 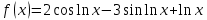 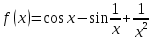 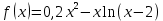 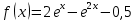 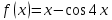 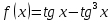 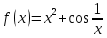 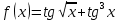 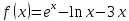 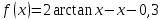 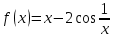 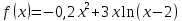 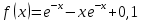 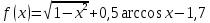 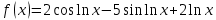 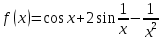 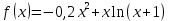 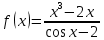 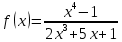 2.2 Решение дифференциального уравнения 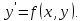 Метод Эйлера 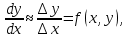 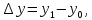 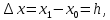 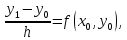 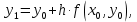 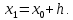 Для 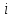 -го шага: -го шага: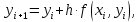 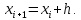 Модифицированный метод Эйлера (вариант 1) 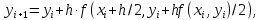 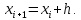 Модифицированный метод Эйлера (вариант 2) 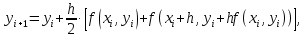 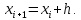 Метод Рунге-Кутты третьего порядка 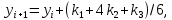 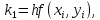 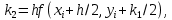 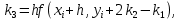 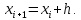 Метод Рунге-Кутты четвертого порядка 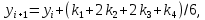 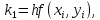 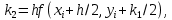 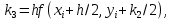 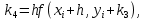 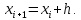 Здесь 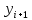 , , 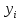 – значения искомой функции в точках – значения искомой функции в точках 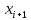 , , 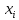 соответственно, индекс соответственно, индекс 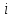 показывает номер шага интегрирования, показывает номер шага интегрирования, 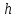 – шаг интегрирования. Начальные условия при численном интегрировании учитываются на нулевом шаге: – шаг интегрирования. Начальные условия при численном интегрировании учитываются на нулевом шаге: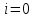 , , 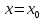 , , 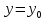 . .Для сравнения предусмотреть построение графика решения, полученного аналитическим способом, и результатов численных методов. 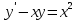 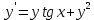 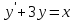 ( 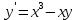 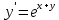 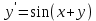 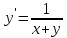 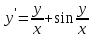 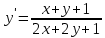 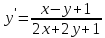 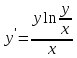 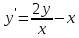 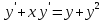 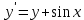 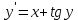 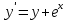 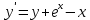 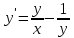 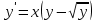 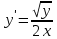 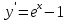 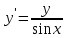 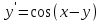 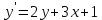 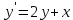 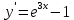 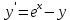 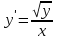 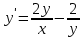 |
