эпюры. Построить эпюры. Решение. Определение опорных реакций Из уравнений равновесия находим Определение

• Название: Решение. Определение опорных реакций Из уравнений равновесия находим Определение
• Анкор: эпюры
• Дата: 16.02.2023
• Размер: 425.5 Kb.
• Имя файла: Построить эпюры.doc
• Тип: Решение; #939865

Построить эпюры   для консольной балки (см. рис. а) и подобрать двутавровое поперечное сечение.



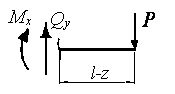                                    а)                                                                    б)              

 

Решение.

1. Определение опорных реакций

Из уравнений равновесия



находим



2. Определение  методом сечения и построение эпюр

Мысленно рассечем балку и рассмотрим правую ее часть (рис. б). Из уравнения равновесия находим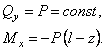



Эпюры представлены на рис. a.

Консольная балка не загружена распределенной нагрузкой, поэтому перерезывающая сила по правилу Журавского постоянна, а момент – прямая, возрастающая с ростом  , поскольку  .

3. Расчет на прочность

Из эпюры   в опасном сечении находим  . Условие прочности записываем в виде

.

Пусть требуется подобрать поперечное сечение в виде стандартного двутавра. Тогда условие прочности представим в виде

.

Пусть  . Тогда  .

Из таблицы сортамента по ГОСТ 8239-89 берем первое большее значение, что соответствует двутавру № 22 с   .  Расчетное  напряжение

 МПа,

что меньше допустимого на 19,2%, это слишком большое недонапряжение, приводящее к дополнительной затрате материала.

Возьмем двутавр № 20 по ГОСТ 8239-89 с  .  Расчетное  напряжение составит

МПа.

Перенапряжение составляет 1%, что меньше допустимого   в инженерных расчетах.

Окончательно выбираем двутавровое сечение балки № 20.

 

Пример 2

Требуется построить эпюры  поперечных  сил и изгибающих моментов и  подобрать   раз­меры   поперечного   сечения  стальной  балки  (рис. 16) для различных форм  сечения : двутавровой  балки ,   балки  прямоугольного  сечения  со сторонами h и b при h/b= 2 и круглого  поперечного   сечения .  Балка  выполнена из ста­ли с допускаемым  напряжением  [σ] =190 МПа ;а=1 м; q=10кН/м.



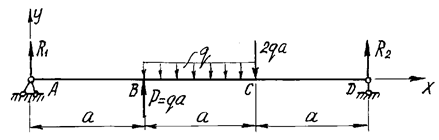Рис. 16. Расчетная схема балки 

 

1. Определение опорных реакций.

На схеме показываем опорные реакцииR₁, H, R₂. Вертикальные реакции направляем вверх и записываем уравнения равновесия:

ΣX=0;     H=0;

ΣM_D=0;    R₁3a+qa∙2a-qa∙1,5a-2qa∙a=0.

Отсюда    R₁=0,5qa.

ΣM_A=0;    R₂3a-2qa∙2a-qa∙1,5a+qa∙a=0.

Отсюда    R₂=1,5qa.

Проверим правильность вычислений,  составив еще одно уравнение равновесия:

ΣY=0;    0,5qa+qa-qa-2qa+1,5qa=0.

Условие равновесия удовлетворяется, реакции  определены правильно.

 

2.Построение эпюрыQ.

Мысленно разбиваем балку на участки. Границами участков являются сечения, в которых к балке приложены сосредоточенные силы или пары сил, на­чинаются или заканчиваются распределенные нагрузки, имеются про­­ме­жуточные шарниры. В рассматриваемой балке граничными сече­ниями будут се­чения A, B, CиD. Для каждого из трех участков запишем аналитическое выражение Q(x). 

УчастокAB, 0.Рассмотрим произвольно выбранное сечение с абсциссой x. Рассекая балку в этом сечении на две части и отбросив правую часть, вычисляем алгебраическую сумму проекций на ось y всех сил, действующих на оставшуюся часть:

Q(x)=R₁=0,5qa.

Поперечная сила не зависит от переменной x на протяжении всего участка, следовательно, эпюра Q ограничена прямой,  параллельной оси абсцисс. Отло­жив от оси эпюры вверх в выбранном масштабе 0,5qa (рис.17), строим эпю­ру на этом участке.

Участок BC,  a y слева от сечения с абсциссой x

Q(x)=0,5qa+qa-q(x-a)=1,5qa-q(x-a).

Полученное выражение является уравнением наклонной прямой, которая может быть построена по двум лежащим на ней точкам. Для ее построения най­дем значения  поперечной  силы на границах участков  балки 

x=a,   Q(a)=1,5qa,

x=2a,  Q(2a)=0,5qa.

Участок CD,   2a

Q(x)=0,5qa+qa-qa-2qa=-1,5qa.

Так как  поперечная  сила не зависит от переменной x, на последнем участке эпюра Q ограничена прямой,  параллельной оси  бал­ки  (см. рис. 17). 

 

3. Построение эпюрыM_z.

Аналитическое выражение для вычисления изгибающего момента в сечении x необходимо записать для каждого участка балки.

Участок AB:

M_z(x)=0,5qa∙x.

На этом участке балки изгибающий момент возрастает по линейному закону и эпюра M_z ограничена наклонной прямой. Вычисляя его значения в сечениях на границах участка,  строим в масштабе (рис. 17)   эпю­ру M_z на сжатом во­ло­кне

x=0,   M_z(0)=0;

x=a,   M_z(a)=0,5qa².

УчастокBC:



Полученное уравнение является уравнением квадратной параболы и, поскольку поперечная сила Q на участке BC не изменяет знак,  экстремума на эпюре M_z не будет.

Определим изгибающий момент на границах участка:

x=a,   M_z(a)=0,5qa²;

x=2a,   M_z(2a)=0,5qa∙2a+qa(2a-a)-

Отложив вверх от оси балки найденные значения,  проводим квадрат­ную па­­­­ра­­болу выпуклостью вверх (навстречу вектору усилия равномерно распределенной нагрузки).

 

УчастокCD:

M_z(x)=0,5qa∙x+qa(x-a)-qa(x-1,5a)-2qa(x-2a).

В пределах последнего участка балки  (2a изгибающий  момент линейно зависит от абсциссы x, и эпюра ограничена прямой линией.

При x=2a,  M_z(2a)=1,5qa²,  при x=3a,  M_z(3a)=0.

Эпюры Q и M_z показаны на рис. 17. 

Для   заданной   расчетной   схемы  двухопорной балки (см. рис.) построить эпюры поперечных сил и изгибающих моментов и подобрать стальную балку двутаврового поперечного сечения, если P= 20 кн =2 т, М =20 кНм =2 тм, q=1,5 кН/м =1,5 т/м, 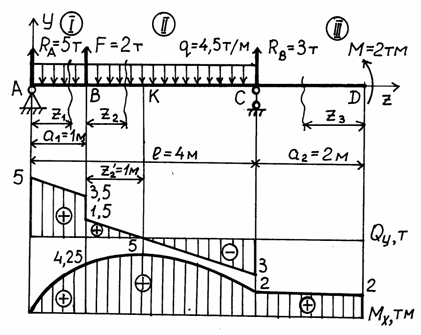 = 1 м,  = 2 м, l = 4 м,  =160 МПа =1600 кг/см².



 

Решение.

1. Вычерчиваем балку в масштабе, наносим все нагрузки и размеры и определяем опорные реакции R_A и R_C  , используя уравнение статического равновесия:

;     ;



;      ;

 

Проверка:  ;

; 

5 - 1,5·4 - 2 + 3 = 0

Наносим вычисленные значения реакций R_A и R_C  на  расчетную   схему .

2. Запишем для каждого участка I, II, III балки уравнения для Q_y  и M_x и, выбрав масштаб, построим их эпюры. Для этого применим метод сечений. На каждом участке проводим произвольные сечения и выбираем начало координат: для участка I – в точке А, для участка II – в точкеВ, для участка III – в точке D. Произвольные сечения каждого участка связываем с выбранным началом отсчета координат Z₁, Z₂ и Z₃. Тогда для каждого участка получим:

Участок I ( ).

; 

.

При составлении уравнения для M_x считаем, что равнодействующая (qZ₁) от равномерно распределенной нагрузки q приложена посередине рассматриваемого участка длиной Z₁, и тогда плечо ее равно Z₁/2.

При Z₁ = 0; Q_y = 5 т, M_x  = 0.

При Z₁ = 1 м; Q_y = 5 – 1,5·1= 3,5 т,  M_x= 5·1 – 5·1²/2 = 4,25 тм.

Участок II  ( ).

;       

.

При составлении уравнений для Q_y и M_x  для участка II видим, что q, приложенная на участке a₁, не зависит от Z₂ (отсчет начинается от точкиВ).

При Z₂ = 0; Q_y  = 5 – 1,5·1 – 2 = 1,5 т, M_x  = 5·1 – 1,5·1/2 =  4,25 тм.

 При Z₂  = 3 м; Q_y = 5 – 1·2 – 1,5·3 = –3 тм. 

M_x = 5·(1+ 3) – 1,5·1(1/2+ 3) –  2·3 – 1,53²/2 = 2 тм.

Построив эпюру Q_y  для этого участка, видим, что она меняет знак с (+) на (). Исследуем на экстремум:

;     ;



При   = 1 м,  M_x = 5·(1 + 1) – 1,5·1(1/2 + 1) – 2·1– 1,51²/2 = 5 тм.

Откладываем от точки В   = 1 м, где Q_y = 0, на эпюре изгибающих моментов откладываем M_x = 5 тм и через полученные три точки проводим параболу – эпюру M_x  .

Участок III (  = 2 м).

Q_y = 0; M_x = М = 2 тм.

Выбираем масштаб, строим эпюры (см. рис.) и проверяем их правильность.

2. Определяем опасное сечение балки – сечение, в котором изгибающий момент принимает максимальное значение по абсолютной величине, если, как в нашем случае, материл балки пластичный.

Опасное сечение K, где  = 5 тм.

Для подбора сечения балки из условия прочности по нормальным напряжениям при изгибе:

                                                                        (1)

получим формулу проектировочного расчета:

 

По сортаменту двутавровых балок (ГОСТ 8239-89) подбираем ближайший больший профиль – двутавр № 24а с осевым моментом сопротивления   = 317 см³.

Максимальные рабочие напряжения будут равны, согласно формулы (1),

 

Недонапряжение составит:

 

Допустимые пределы отклонения  .
        

z

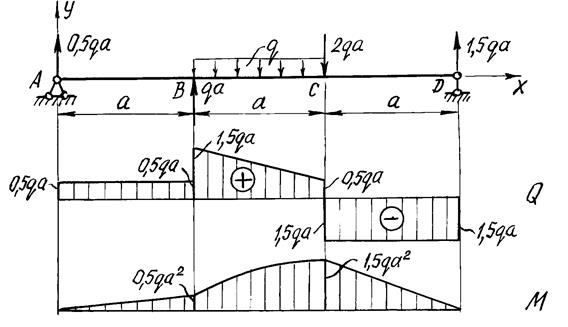Рис. 17. Расчетная схема балки. Эпюры поперечных сил и изгибающих моментов

 

По эпюре M_z находим опасное  сечение   балки  -  сечение , в котором изгибающий момент максимален по абсолютной величине. Для задан­ной  балки изгибающий момент в опасном  сечении    = M_z(2a)=1,5qa² или после подстановки числовых значений  =1,5∙10∙1²=15кНм.

Из условия прочности определим требуемый момент сопротивления сечения



Номер двутавра находим по расчетному значению момента сопротивления W_z, используя таблицы сортамента прокатной стали.

Внимание! В таблицах сортамента прокатной стали (см. приложение) оси zсоответствует ось x , это означает, что W_z=W_x.

Наиболее близок к требуемому момент сопротивления двутавра №14, равный W_x= 81,7 см³. Выбрав это  сечение , определяем нормальные  напряжения  в поперечном   сечении   балки :



 Подбираем  прямоугольное сечение, момент сопротивления которого определяется с учетом того, что h=2b:



Отсюда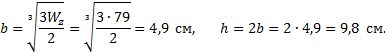



Круглое  поперечное   сечение  имеет момент сопротивления



Диаметр круга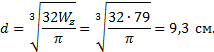



Рассмотрим второй метод построения эпюр внутренних усилий, дей­ствующих в  сечениях   балки . Он  состоит в том, что попе­реч­ные­ силы и из­­­­ги­ба­ющие моменты вычисляются на границах участков без записи уравнений Q(z), M(z), а соответствующие эпюры строятся на основании диф­фе­рен­циальных зависимостей междуQ, M, q:



Зависимости (1) позволяют установить следующие характерные  особенно­сти эпюр  поперечных  сил и изгибающих моментов:

На участках, где нет распределенной нагрузки,  эпюра Q ограничена пря­мыми, параллельными оси  балки , а эпюра M - наклонными прямыми.

На участках, где приложена равномерно распределенная нагрузка интенсивностью q, эпюра Q ограничена наклонными прямыми, а эпюра M - квадратными параболами,  выпуклость которых направлена навстречу вектору рав­но­мер­но распределенной нагрузки.

На участках,  где Q >0,   изгибающий момент возрастает; если Q<0 - из­ги­бающий момент убывает.

В  сечениях ,   где к  балке  приложены сосредоточенные силы, на эпюре Q бу­дут скачки на величину приложенных сил, а на эпюре M- переломы, острие которых направлено против действия этих сил.

В  сечениях , где к  балке  приложены пары сил (сосредоточенные мо­менты), на эпюре M будут скачки на величину этих моментов.

Если на участке  балки  имеется равномерно распределенная нагрузка и эпюра Q в пределах участка изменяет знак, то в  сечении , где Q =0, на эпюре M_z будет экстремум.