Примеры решения задач по оптике. Решение Освещенность величина, обратно пропорциональная площади. Площадь прямоугольного объекта s 5 8 4 (м 2 )

• Название: Решение Освещенность величина, обратно пропорциональная площади. Площадь прямоугольного объекта s 5 8 4 (м 2 )
• Анкор: Примеры решения задач по оптике.docx
• Дата: 21.03.2018
• Размер: 402.78 Kb.
• Имя файла: Примеры решения задач по оптике.docx
• Тип: Решение; #17017
• страница: 6 из 7

Практическое занятие №4.
Определение параксиальных параметров линз различных типов

4.3. Определение параксиальных параметров линз-менисков

Выпукло-вогнутые мениски

Ниже представлено описание конструктивных параметров оптических элементов, достаточное для определения типа. Необходимо отметить, что в некоторых задачах для определения знаков конструктивных параметров дается тип линзы.

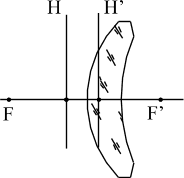
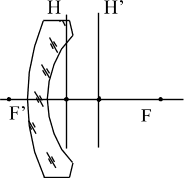
Выпукло-вогнутый собирающий мениск (положительный)

Выпукло-вогнутый рассеивающий мениск (отрицательный)

Вогнуто-выпуклые мениски

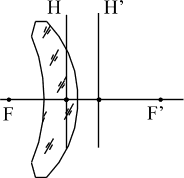
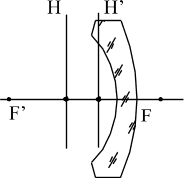
Вогнуто-выпуклый собирающий мениск (положительный)

Вогнуто-выпуклый рассеивающий мениск (отрицательный)

Задача

Изображение находится на расстоянии S'=40.25 от вогнуто-выпуклого мениска. Параметры линзы: d=10, радиусы : 100 и 15, n=1.5. Найти положение предмета (s).

Решение:

В данном случае сразу же необходимо разобраться со знаками радиусов. R₁=-100, R₂=-15.

Параксиальные характеристики системы: f'=33.96; S_F= -26.42; S'_F= 35.09

Воспользуемся для расчетов формулой Ньютона: f·f'=z·z'

s'=z'+ S'_F, значит, z'=s'-S'_F=40.25-35.09=5.16

По формуле Ньютона z=f·f'/z'=-223.58.

s=S_F+z=-26.42-223.56=-250 мм

Ответ: S=-250 мм.

4.4. Определение параксиальных параметров концентрических линз

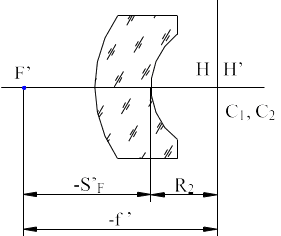
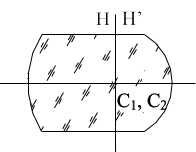
Концентрические линзы - это линзы, у которых центры кривизны обеих поверхностей совпадают. Следовательно, толщина линзы рассчитывается по формуле:



При определении параксиальных параметров концентрических линз характерно совпадение главных плоскостей в центре кривизны обеих поверхностей:

Оптическая сила: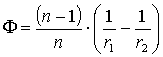

Задача

Фокусное расстояние лизы-шара f'=75 мм. Определить радиус шара, если показатель преломления n=1.5.

Решение:

Из выражения:

Ф=2·(n-1)/(n·r) определим фокусное расстояние линзы-шара:

f'=(n·r)/2·(n-1)

Следовательно, радиус: r=f'·2·(n-1)/n

Расчеты:

r=75·2·(1.5-1)/1.5=50 (мм)

Ответ: Радиус линзы-шара 50 мм.