Насосы. Решение Площадь поперечного сечения плунжера f (d)4 (3,140,1)4 0,00785 м2
 Скачать 91.82 Kb. Скачать 91.82 Kb.
|
|
Задачи для самостоятельной работы студентов (с решениями) По дисциплине: «Гидравлические и пневматические системы» Подготовила преподаватель Осипова Н.М. Примеры задач по расчету и подбору насосов с решениями Задача 1 Плунжерный насос одинарного действия обеспечивает расход перекачиваемой среды 1 м3/ч. Диаметр плунжера составляет 10 см, а длинна хода – 24 см. Частота вращения рабочего вала составляет 40 об/мин.Требуется найти объемный коэффициент полезного действия насоса. 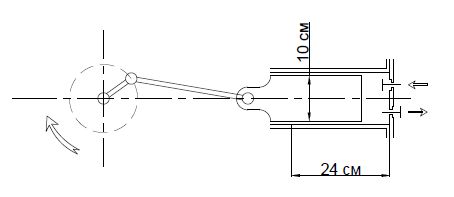 Решение: Площадь поперечного сечения плунжера : F = (π·d²)/4 = (3,14·0,1²)/4 = 0,00785 м²2 Выразим коэффициент полезного действия из формулы расхода плунжерного насоса: ηV = Q/(F·S·n) = 1/(0,00785·0,24·40) · 60/3600 = 0,88 Плунжерный насос одинарного действия обеспечивает расход перекачиваемой среды 1 м3/ч. Диаметр плунжера составляет 10 см, а длинна хода – 24 см. Частота вращения рабочего вала составляет 40 об/мин.Требуется найти объемный коэффициент полезного действия насоса.  Решение: Площадь поперечного сечения плунжера : F = (π·d²)/4 = (3,14·0,1²)/4 = 0,00785 м²2 Выразим коэффициент полезного действия из формулы расхода плунжерного насоса: ηV = Q/(F·S·n) = 1/(0,00785·0,24·40) · 60/3600 = 0,88 Задача 2 Двухпоршневой насос двойного действия создает напор 160 м при перекачивании масла с плотностью 920 кг/м3. Диаметр поршня составляет 8 см, диаметр штока – 1 см, а длинна хода поршня равна 16 см. Частота вращения рабочего вала составляет 85 об/мин. Необходимо рассчитать необходимую мощность электродвигателя (КПД насоса и электродвигателя принять 0,95, а установочный коэффициент 1,1). 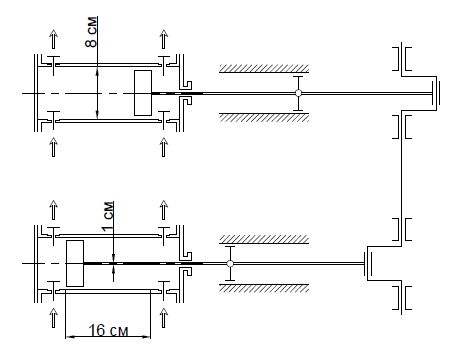 Решение: Площади попреречного сечения поршня и штока: F = (3,14·0,08²)/4 = м² F = (3,14·0,01²)/4 = м² Производительность насоса находится по формуле: Q = N·(2F-f)·S·n = м³/час Далее находим полезную мощность насоса: NП = 920·9,81·0,0045195·160 = С учетом КПД и установочного коэффициента получаем итоговую установочную мощность: NУСТ = 6526,3/(0,95·0,95)·1,1 = 7954,5 Вт = 7,95 кВт Задача 3 Трехпоршневой насос перекачивет жидкость с плотностью 1080 кг/м3 из открытой емкости в сосуд под давлением 1,6 бара с расходом 2,2 м3/час. Геометрическая высота подъема жидкости составляет 3,2 метра. Полезная мощность, расходуемая на перекачивание жидкости, составляет 4 кВт. Необходимо найти величину потери напора. Решение: Найдем создаваемый насосом напор из формулы полезной мощности: H = NП/(ρ·g·Q) = 4000/(1080·9,81·2,2)·3600 = 617,8 м Подставим найденное значение напора в формулу напора, выраженую через разность давлений, и найдем искомую величину: hп = H - (p2-p1)/(ρ·g) - Hг = 617,8 - ((1,6-1)·105)/(1080·9,81) - 3,2 = 69,6 м Задача 4 Реальная производительность винтового насоса составляет 1,6 м3/час. Геометрические характеристики насоса: эксцентриситет – 2 см; диаметр ротора – 7 см; шаг винтовой поверхности ротора – 14 см. Частота вращения ротора составляет 15 об/мин. Необходимо определить объемный коэффициент полезного действия насоса. Решение: Выразим искомую величину из формулы производительности винтового насоса: ηV = Q/(4·e·D·T·n) = 1,6/(4·0,02·0,07·0,14·15) · 60/3600 = 0,85 Задача 5 Необходимо рассчитать напор, расход и полезную мощность центробежного насоса, перекачивающего жидкость (маловязкая) с плотностью 1020 кг/м3 из резервуара с избыточным давлением 1,2 бара а резервуар с избыточным давлением 2,5 бара по заданному трубопроводу с диаметром трубы 20 см. Общая длинна трубопровода (суммарно с эквивалентной длинной местных сопротивлений) составляет 78 метров (принять коэффициент трения равным 0,032). Разность высот резервуаров составляет 8 метров. 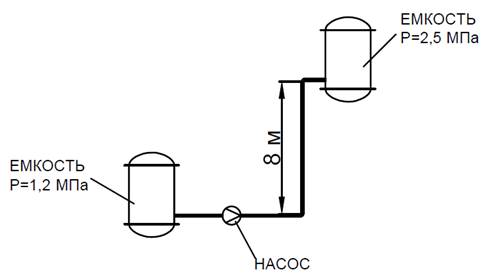 Решение: Для маловязких сред выбираем оптимальную скорость движения в трубопроводе равной 2 м/с. Рассчитаем расход жидкости через заданный трубопровод: Q = (π·d²) / 4·w = (3,14·0,2²) / 4·2 = 0,0628 м³/с Скоростной напор в трубе: w²/(2·g) = 2²/(2·9,81) = 0,204 м При соответствующем скоростном напоре потери на трение м местные сопротивления составят: HТ = (λ·l)/dэ · [w²/(2g)] = (0,032·78)/0,2 · 0,204 = 2,54 м Общий напор составит: H = (p2-p1)/(ρ·g) + Hг + hп = ((2,5-1,2)·105)/(1020·9,81) + 8 + 2,54 = 23,53 м Остается определить полезную мощность: NП = ρ·g·Q·H = 1020·9,81·0,0628·23,53 = 14786 Вт Задача 6 Целесообразна ли перекачка воды центробежным насосом с производительностью 50 м3/час по трубопроводу 150х4,5 мм? Решение: Рассчитаем скорость потока воды в трубопроводе: Q = (π·d²)/4·w w = (4·Q)/(π·d²) = (4·50)/(3,14·0,141²) · 1/3600 = 0,89 м/с Для воды скорость потока в нагнетательном трубопроводе составляет 1,5 – 3 м/с. Получившееся значение скорости потока не попадает в данный интервал, из чего можно сделать вывод, что применение данного центробежного насоса нецелесообразно. Задача 7 Определить коэффициент подачи шестеренчатого насоса. Геометрические характеристики насоса: площадь поперечного сечения пространства между зубьями шестерни 720 мм2; число зубьев 10; длинна зуба шестерни 38 мм. Частота вращения составляет 280 об/мин. Реальная подача шестеренчатого насоса составляет 1,8 м3/час. Решение: Теоретическая производительность насоса: Q = 2·f·z·n·b = 2·720·10·0,38·280·1/(3600·106) = 0,0004256 м³/час Коэффициент подачи соответственно равен: ηV = 0,0004256/1,8·3600 = 0,85 Задача 8 Насос, имеющий КПД 0,78, перекачивает жидкость плотностью 1030 кг/м3 с расходом 132 м3/час. Создаваемый в трубопроводе напор равен 17,2 м. Насос приводится в действие электродвигателем с мощностью 9,5 кВт и КПД 0,95. Необходимо определить, удовлетворяет ли данный насос требованиям по пусковому моменту. Решение: Рассчитаем полезную мощность, идущую непосредственно на перекачивание среды: NП = ρ·g·Q·H = 1030·9,81·132/3600·17,2 = 6372 Вт Учтем коэффициенты полезного действия насоса и электродвигателя и определим полную необходимую мощность электродвигателя: NД = NП/(ηН·ηД) = 6372/(0,78·0,95) = 8599 Вт Поскольку нам известна установочная мощность двигателя, определим коэффициент запаса мощности электродвигателя: β = NУ/NД = 9500/8599 = 1,105 Для двигателей с мощностью от 5 до 50 кВт рекомендуется выдирать пусковой запас мощности от 1,2 до 1,15. Полученное нами значение не попадает в данный интервал, из чего можно сделать вывод, что при эксплуатации данного насоса при заданных условиях могут возникнуть проблемы в момент его пуска. Задача 9 Центробежный насос перекачивает жидкость плотностью 1130 кг/м3 из открытого резервуара в реактор с рабочим давлением 1,5 бар с расходом 5,6 м3/час. Геометрическая разница высот составляет 12 м, причем реактор расположен ниже резервуара. Потери напора на трение в трубах и местные сопротивления составляет 32,6 м. Требуется определить полезную мощность насоса. 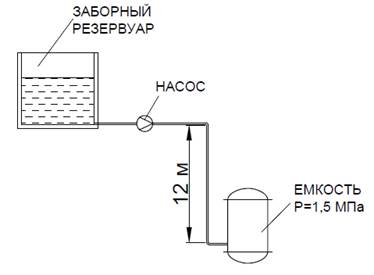 Решение: Рассчитаем напор, создаваемый насосом в трубопроводе: H = (p2-p1)/(ρ·g) + Hг + hп = ((1,5-1)·105)/(1130·9,81) - 12 + 32,6 = 25,11 м Полезная мощность насоса может быть найдена по формуле: NП = ρ·g·Q·H = 1130·9,81·5,6/3600·25,11 = 433 Вт Задача 10 Определить предельное повышение расхода насоса, перекачивающего воду (плотность принять равной 1000 кг/м3) из открытого резервуара в другой открытый резервуар с расходом 24 м3/час. Геометрическая высота подъема жидкости составляет 5 м. Вода перекачивается по трубам 40х5 мм. Мощность электродвигателя составляет 1 кВт. Общий КПД установки принять равным 0,83. Общие потери напора на трение в трубах и в местных сопротивлениях составляет 9,7 м.  Решение: Определим максимальное значение расхода, соответствующее максимально возможной полезной мощности, развиваемой насосом. Для этого предварительно определим несколько промежуточных параметров. Рассчитаем напор, необходимый для перекачивания воды: H = (p2-p1)/(ρ·g) + Hг + hп = ((1-1)·105)/(1000·9,81) + 5 + 9,7 = 14,7 м Полезная мощность, развиваемая насосом: NП = Nобщ/ηН = 1000/0,83 = 1205 Вт Значение максимального расхода найдем из формулы: NП = ρ·g·Q·H Найдем искомую величину: Qмакс = NП/(ρ·g·H) = 1205/(1000·9,81·14,7) = 0,00836 м³/с Расход воды может быть увеличен максимально в 1,254 раза без нарушения требований эксплуатации насоса. Qмакс/Q = 0,00836/24·3600 = 1,254 Задача11 При гидравлическом испытании системы объединенного внутреннего противопожарного водоснабжения допускается падение испытательного дав- ления в течение 10 мин на Δр = 4,9 х 104 Па. Определить допускаемую вели- чину утечки ΔW в течение 10 мин при гидравлическом испытании системы вместимостью W = 80 м3 . Деформацией трубопроводов пренебречь. Коэффи- циент объемного сжатия воды β = 0,5 х 10-9 1/Па. Решение: Коэффициент объемного сжатия определяется по формуле: W p W , откуда допускаемая величина утечки в течение 10 мин при гидравличе- ском испытании системы: W p 0,5 10 80 4,9 10 0,00196 м3-9 4 W = 1,96 л Задача 12 Определить усилия, необходимые для открытия всасывающего клапана пожарного насоса, если длина рукава Н = 7 м, d = 125 мм, а глубина погру- жения всасывающего клапана h = 2 м. Диаметр клапана D = 200 мм. Решение: 3 S1 = πD2 / 4 = (3,14 х 0,22 ) / 4 = 0,0314 м2 , S2 = πd2 / 4 = (3,14 х 0,1252 ) / 4 = 0,0124 м 2 , F1 = ρgНS1 = 1000 х 9,81 х 7 х 0,0314 = 2,156 кН, F2 = ρg (Н – h) S2 = 1000 х 9,81 х 5 х 0,0124 = 0,608 кН, F = F1 – F2 = 1,54 кН Задача 13 Круглая труба водовыпуска из пожарного водоема диаметром d = 1 м за- крыта наклонной крышкой. Угол наклона крышки α по отношению к урезу воды равен 600 . Ось водовыпуска находится на глубине Н = 2 м. Определить силу давления и центр давления воды на крышку. d, мм D, мм H, м h, м 125 200 8 1,5 4 Решение: Сила давления на крышку: 4sin 60 3,14 1 1000 9,81 2 4sin 2 2 d P ghc S gH 17,75 кН Центр давления воды на крышку: sin 60 2 sin Н уц 2,35 м Ответ: Р = 17,75 кН; уц = 2,35 м. Задача 13 Определить скорость течения жидкости с помощью трубки Пито и диа- метр трубы, если уровень жидкости в трубке поднялся на высоту hv. hv = 0,09 м; Q = 0,02 м3 /с Решение: Составим уравнение Бернулли для сечения I-I и II-II: 5 2 g ат 2 P h h g V g Р gh v ат , откуда 1,33 м/с 0,09 9,81 2 2ghv V Определим площадь трубы: S = Q / V = 0,02 / 1,33 = 0,015 м S = πd2 / 4, откуда искомый диаметр трубы 3,14 4 4 0,015 S d 0,14 м Ответ: V = 1,33 м/с; d = 0,14 м Задача 14 Сопротивление участка водопроводной трубы с арматурой необходимо перед установкой проверить в лаборатории путем испытаний на воздухе. Определить, с какой скоростью следует вести продувку, сохраняя подо- бие режимов движения (Reн = Reм), если скорость воды в трубе должна быть 2,5 м/с. Какова будет потеря напора hx при работе трубы на воде с указанной скоростью, если при испытании на воздухе потеря давления оказалась равной ΔРм = 8,35 кПа, νводы = 10-6 м 2 /с, νвоздуха = 15,6 х 10-6 м 2 /с, ρводы = 103 кг/м3 , ρвоздуха = 1,2 кг/м3 , t = 20 0С. Решение: Определим скорость продувки из гидравлического подобия Reн = Reм: м м н н V d V d , -6 -6 н н м 10 2,5 15,6 10 м V 39 м/сV Потери давления: 2d 2 м Vм l Рм , откуда 6 2 3 2 м м м 1,2 39 Р 2 8,35 10 2 l d V d 9,15d Потеря напора: 2 9,81 d 9,15 2,5 2gd 2 2 l Vн d hx 2,91 м Ответ: Vм = 39 м/с; hx = 2,91 м |
