математика практическая 3. математика практ. раб. 3. Решение По формуле сочетаний выбрать элементов из можно следующим числом способов Тогда при 34 и 2 получим
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
|
Задание №1 В домашней библиотеке у Василия Петровича собрано 34 книги по научной фантастике. Он хочет взять с собой в отпуск 2 книги для чтения. Сколькими способами Василий Петрович может это сделать? Решение По формуле сочетаний выбрать 𝑟 элементов из 𝑛 можно следующим числом способов: Тогда при 𝑛 = 34 и 𝑟 = 2 получим: Ответ: 𝑁 = 561  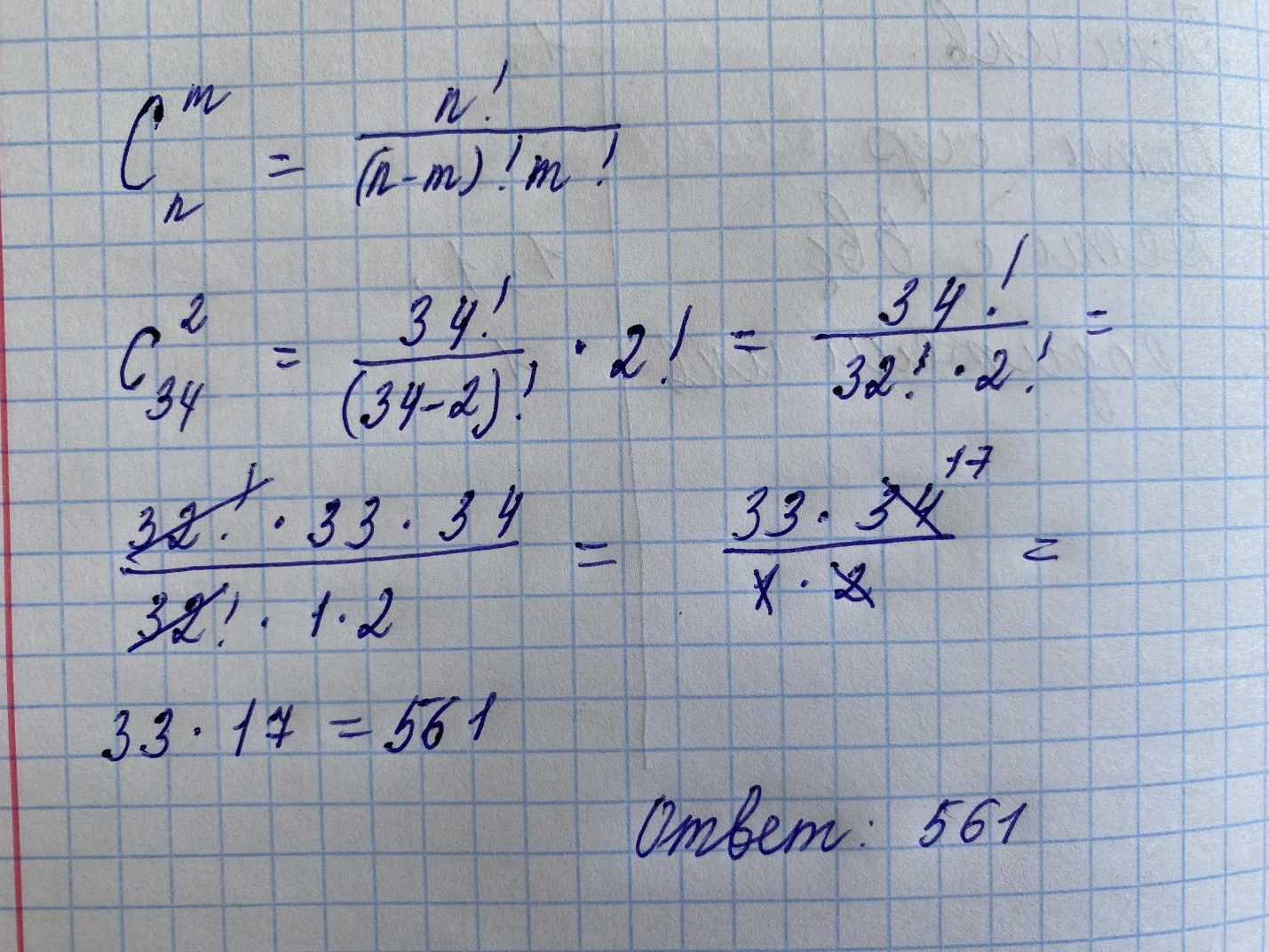 В кино отправились 5 друзей. Сколькими разными способами они могут встать в очередь на кассе? 120 способов. Пошаговое объяснение: 5*4*3*2*1 = 120 способов Таблица, размером 99*99, раскрашена в шахматном порядке в белый и черный цвета. Верхняя левая клетка – белая. Сколькими способами можно указать в таблице два квадрата – белый и черный? 24014900 способов Пошаговое объяснение: В таблице 99*99 = 9801 клеток. Из них 4900 черных и 4901 белых, потому что все угловые - белые. Вариантов выбрать 1 белую и 1 черную клетку: N = 4900*4901 = 24014900 Задание №2 При игре в кости бросаются два игральных кубика и подсчитывается сумма выпавших очков. Найти вероятность событий: А – сумма равна 4; В – сумма больше 7. Решение По классическому определению вероятности, вероятность события 𝐴 равна где 𝑚 – число благоприятных исходов, 𝑛 – общее число исходов. Игральная кость при двух бросках может выпасть следующими вариантами: Общее число 𝑛 таких выпадений равно: а) Выберем те пары значений, которые удовлетворяют заданному условию: Число благоприятных исходов равно: Вероятность события 𝐴 – сумма выпавших очков равна 4, равна: б) Выберем те пары значений, которые удовлетворяют заданному условию: Число благоприятных исходов равно: Вероятность события 𝐵 – сумма выпавших очков больше 7, равна: Ответ: 𝑃(𝐴) = 1 12 ; 𝑃(𝐵) = 5 12  Из имеющихся 20 телевизоров 14 готовы к продаже, а 6 требуют дополнительной регулировки. Найти вероятности событий: А – из случайно отобранных 4 телевизоров все хорошие, В – три хорошие и один нет, С – один хороший и три нет, D – хороших нет. Большое событие состоит из двух маленьких независимых, вот его формула: Р(С)=Р(А)*Р(В) Больших событий у нас несколько, проще найти вероятность, что будет хороший телевизор и плохой. Чтобы найти маленькое событие: Р(А)= благоприятные исходы(m)/кол-во всего исходов(n) Всего исходов 20, т.к. 20 телевизоров. Р(х)=14/20= 0,7 (14 т.к 14 хороших телевизоров, это у нас благоприятные) Р(п)=6/20= 0,3 (6 т.к. 6 плохих телевизоров, это у нас благоприятные) Теперь будет подставлять под задание. А. Большое событие: из случайно отобранных 4 телевизоров все хорошие Подставим в формулу и получим: Р(С)= 1 телевизор хороший и второй и третий и четвёртый И- умножение Получаем: Р(С)=Р(х)*Р(х)*Р(х)*Р(х) Выше мы уже узнали вероятность, просто подставляем. Р(С)= 0,7*0,7*0,7*0,7=0,2401 В. Большое событие: три хорошие и один нет Подставим в формулу и получим: Р(С)= 1 телевизор хороший и второй и третий и четвёртый плохой И- умножение Получаем: Р(С)=Р(х)*Р(х)*Р(х)*Р(п) Р(С)= 0,7*0,7*0,7*0,3=0,1372 C. Большое событие: один хороший и три нет Подставим в формулу и получим: Р(С)= 1 телевизор плохой и второй и третий и четвёртый хороший И- умножение Получаем: Р(С)=Р(п)*Р(п)*Р(п)*Р(х) Р(С)= 0,3*0,3*0,3*0,7=0,0189 D. Большое событие: хороших нет Подставим в формулу и получим: Р(С)= 1 телевизор плохой и второй и третий и четвёртый И- умножение Получаем: Р(С)=Р(п)*Р(п)*Р(п)*Р(п) Р(С)= 0,3*0,3*0,3*0,3=0,0081 Туристическая группа состоит из 11 юношей и 5 девушек. По жребию (случайным образом) выбирают 3 дежурных. Найти вероятность того, что будут выбраны 2 девушки и 1 юноша. Ответ: p=11/56. Пошаговое объяснение: Количество способов n, которыми можно выбрать 3 человека из 16, определяется по формуле n=C(16,3), где C(m,k) – число сочетаний из n по k. Количество благоприятных способов m=C(5,2)*(C11,1). Отсюда искомая вероятность p=m/n=11/56. Решение Основное событие 𝐴 – будут выбраны 2 девушки и 1 юноша. По классическому определению вероятности, вероятность события 𝐴 равна 𝑛 где 𝑚 – число благоприятных исходов, 𝑛 – общее число исходов. Число возможных способов выбрать 3 человека из 16 равно (по формуле сочетаний). Благоприятствующими являются случаи, когда из общего числа 11 юношей выбрали 1 и из общего числа 5 девушек выбрали 2 (это можно сделать способами и способами соответственно). Вероятность события 𝐴 равна:  |
