Решение, получаемое численным методом, обычно
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
|
Для сравнения рассмотренных методов используются два параметра: – сложность алгоритма. – время решения уравнения на компьютере. Если сравнивать по сложности алгоритмов, то все методы достаточно просты. Можно выделить метод половинного деления, поскольку он всегда сходится, если функция непрерывна и имеет корень на рассматриваемом интервале. В этом случае не нужно исследовать функцию и выбирать первое приближение для , но метод требует большего количества итераций по сравнению с другими методами. Время решения уравнений зависит от количества итераций и времени, которое затрачивается на одну итерацию. А время одной итерации, в свою очередь, зависит от того, сколько раз вычисляется функция и ее производная на одной итерации. Если сравнивать количество итераций, то все зависит от вида функции. В большинстве случаев меньше всего итераций требует метод касательных (Ньютона), даже при том условии, что метод требует вычисления производной на каждой итерации, и время, затраченное на решение обычно меньше, чем у других методов. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ Система линейных алгебраических уравнений (СЛАУ), состоящая из n уравнений, может быть записана в следующем виде 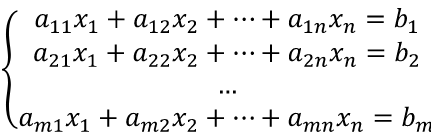 или может быть представлена в матричной форме Ax = b: где 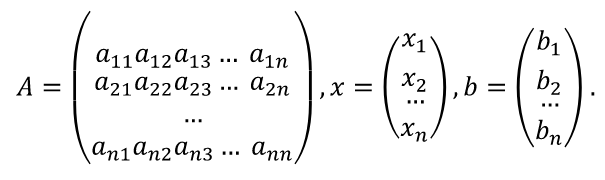 Для СЛАУ a11, a12, Ann… – это постоянные коэффициенты, X1, X2, X3… – неизвестные, b1, b2, b3 … bn– свободные члены системы. Решением СЛАУ является такая совокупность значений неизвестных X1, X2 .. Xn, которая каждое уравнение системы обращает в верное тождество. Диагональ матрицы, проходящая слева направо, называется главной диагональю. Если все элементы матрицы, находящиеся ниже главной диагонали, равны нулю, то такая матрица называется треугольной Необходимым и достаточным условием существования единственного решения системы линейных уравнений является неравенство нулю определителя матрицы коэффициентов. В случае равенства нулю определителя матрица называется вырожденной . При этом система либо не имеет решения, либо имеет их бесконечное множество. Система, в которой определитель близок, но не равен нулю, называется плохо обусловленной системой Непосредственный расчет определителей для больших N (матриц) является очень трудоемким по сравнению с вычислительными методами. В настоящее время известны многочисленные приближенные методы решения систем линейных алгебраических уравнений, которые делятся на две большие группы: прямые методы и методы итераций. Прямые методы всегда гарантируют получение решения, если оно существует, однако для больших требуется большое количество операций, и возникает опасность накопления погрешностей. Этого недостатка лишены итерационные методы, но зато они не всегда сходятся и могут применяться, лишь для систем определенных классов. Рассмотрим наиболее распространенные методы. Метод Крамера Метод Крамера является прямым методом. Это способ решения систем линейных алгебраических уравнений с числом уравнений, равным количеству неизвестных с ненулевым главным определителем матрицы, коэффициентов системы. Обычно метод Крамера применяется для систем с очень малым количеством уравнений. Решение представляется в виде где – определитель системы; – определители, получающиеся из определителя путем замены его i– го столбца столбцом свободных членов. Система N линейных уравнений сводится к вычислению N+1 определителя порядка N. Метод Гаусса принадлежит к группе прямых методов и является классическим методом решения системы линейных алгебраических уравнений. Метод основан на приведении матрицы к треугольному виду. Рассмотрим этот метод на примере системы трех уравнений, а затем распространим его на систему N уравнений: 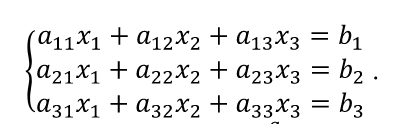 Умножим первое уравнение на a21 / a11 и вычтем его из второго уравнения. Затем полученное уравнение поставим вместо второго. Тогда первый коэффициент полученного второго уравнения станет равным нулю. То же самое проделаем с третьим уравнением, умножив исходное первое уравнение на a31 / a11 . В результате система будет преобразована к следующему виду: 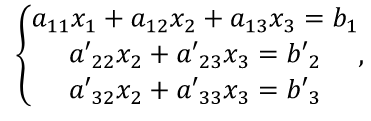 где , , , , , . 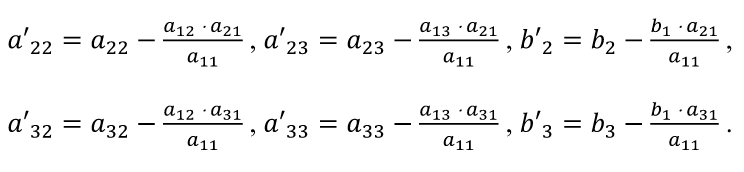 Обобщим эти формулы для системы N уравнений. Обозначим через –i номер строки, j– номер столбца. 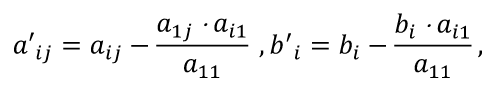 где i, j = 2...n Теперь из третьего уравнения необходимо исключить член, содержащий X2. Для этого умножим второе уравнение на и вычтем е 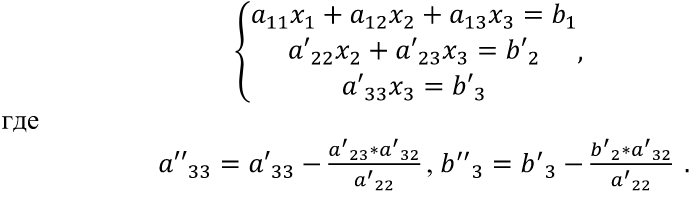 го из третьего. В результате получим го из третьего. В результате получимгде , Теперь матрица системы приведена к треугольному виду, и из третьего уравнения можно найти , затем подставить его во второе уравнение и найти X3 из него и т.д. 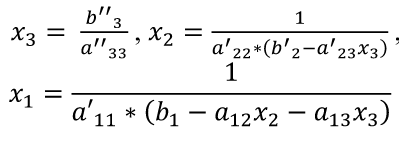 Аналогично строится алгоритм для системы с произвольным числом уравнений, который включает два этапа: 1. Прямой ход – приведение матрицы системы к треугольному виду. 2. Обратный ход – вычисление искомых неизвестных. Метод простых итераций Метод простых итераций является одним из простейших итерационных методов. Рассмотрим метод также на примере трех линейных уравнений, а затем применим на систему N уравнений : 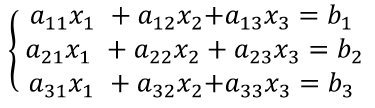 Предполагается, что диагональные элементы отличны от нуля, в противном случае надо переставить уравнения. Выразим неизвестные из уравнений ; Для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов были не меньше сумм модулей всех остальных коэффициентов: 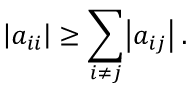 Это условие является достаточным для сходимости метода итерации, но не является необходимым, т.е. для некоторых систем процесс сходится и при нарушении этого условия. В случае системы линейных уравнений, чтобы получить сходимость и верное решение, необходимо соблюдать условие: на главной диагонали системы должны располагаться максимальные элементы каждой строки (т.е. при необходимости надо переставить строки местами). Метод прогонки Метод прогонки используется для решения систем линейных уравнений с трехдиагональной матрицей: 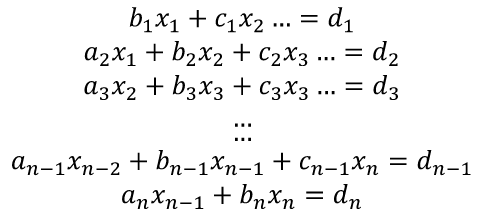 На главной диагонали находятся коэффициенты bi Метод состоит из двух этапов: прямой и обратной прогонки. При прямой прогонке каждое Xi выражается через Xi +1 с помощью прогоночных коэффициентов Ai, Bi: линейных уравнений 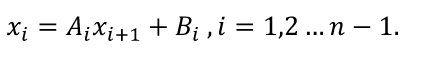 Обратная прогонка состоит в последовательном вычислении неизвестных Вычислим из последнего уравнения:  Необходимо отметить возможность появления деления на нуль в формулах. Доказано, что, если причем хотя бы при одном было строгое неравенство, деления на нуль не возникает, и система имеет единственное решение. Это условие также обеспечивает устойчивость метода относительно погрешностей округлений. Это позволяет использовать метод для систем большой размерности. Условие устойчивости является достаточным, но не необходимым. В некоторых случаях для хорошо обусловленных систем метод устойчив и при нарушении этого условия. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ Запишем систему нелинейных уравнений в общем виде . 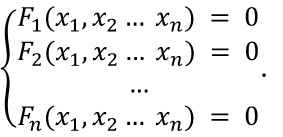 На данный момент не существует прямых методов решения систем нелинейных уравнений в общем виде. Однако для решения часто используются итерационные методы. Метод простых итераций Выразим неизвестные в системе и представим в следубщем виде: 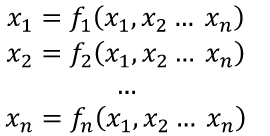 Итерационный процесс продолжается до тех пор, пока не будет выполнено следующее условие: 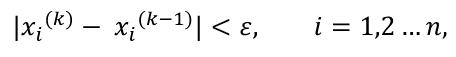 где n –количество уравнений. Если условие не выполняется, итерации повторяются, приняв Для того чтобы не проверять условие для всех уравнений, условие окончания итераций можно записать в следующем виде: 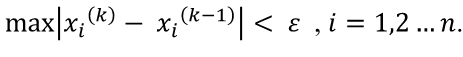 Метод Ньютона-Рафсона Метод Ньютона-Рафсона обладает более быстрой сходимостью. В основе метода лежит использование разложения функций в ряд Тейлора, причем члены, содержащие вторые и более высоких порядков производные, отбрасываются. Будем рассматривать систему нелинейных уравнений также в общем виде. Пусть точное значение корней системы равно x1, x2.. Xn, а приближенные значения – 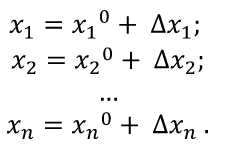 Тогда имеем: Проведем разложение левых частей уравнений в ряд Тейлора, ограничиваясь лишь первыми членами относительно приращений: Поскольку левые части уравнений равны нулю, то приравниваем нулю и правые части. В результате получим систему линейных уравнений (4.3) относительно приращений : 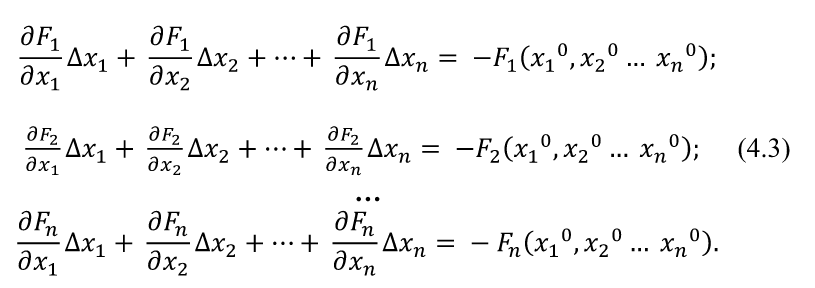  Такая матрица называется матрицей Якоби , а определитель – якобианом. Для существования единственного решения необходимо и достаточно чтобы j <> 0 Производная рассчитывается следующим образом: задаются начальные приближения и вычисляются производные, входящие в систему (6) при этих значениях. Далее решается система относительно приращений АППРОКСИМАЦИЯ ФУНКЦИЙ Задача приближения (аппроксимации) функций заключается в том, чтобы для данной функции построить другую, отличную от нее функцию, значения которой достаточно близки к значениям данной функции. В основном аппроксимация функции применяется в случае, если: 1. Функция задана таблицей в конечном множестве точек, а вычисления нужно произвести в других точках. 2. Функция задана аналитически, но ее вычисление по формуле затруднительно. При решении задачи поиска приближенной функции возникают следующие проблемы: 1. Необходимо выбрать вид приближенной функции. Для приближения широко используются многочлены, тригонометрические функции, показательные функции и т. д. 2. Необходимо выбрать критерий близости исходной и приближенной функции. Это может быть требование совпадения обеих функций в узловых точках (задача интерполяции), минимизация среднеквадратического уклонения (метод наименьших квадратов) и др. 3. Необходимо указать правило (алгоритм), позволяющее с заданной точностью найти приближение функции. Теорема Вейерштрасса. Если функция f(x) непрерывна на отрезке [a, b] , то для любого E>0 существует многочлен степени m = m(E) абсолютное отклонение которого от функции f(x) на отрезке [a, b] меньше . Т.е. любую функцию можно как угодно точно аппроксимировать многочленом, но теорема ничего не говорит, ни о способах нахождения этого многочлена, ни о количестве точек, ни об их расположении. Определение аппроксимирующей функции представляет собой задание вида функции и нахождение ее коэффициентов. При аппроксимации многочленами предварительно задаются степенью многочлена и находят его коэффициенты. При этом отклонение должно быть наименьшим. Метод наименьших квадратов Метод наименьших квадратов – . На практике стараются подобрать аппроксимирующий многочлен как можно меньшей степени, обычно m=1,2,3 Мерой отклонения многочлена о при среднеквадратичном приближении является S, равная сумме квадратов разностей между значениями многочлена и функции в заданных точках: 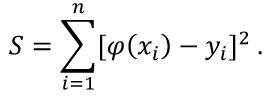 Коэффициенты многочлена надо подобрать так, чтобы величина была минимальной. В этом состоит метод наименьших квадратов. Запишем сумму квадратов отклонений для всех точек: 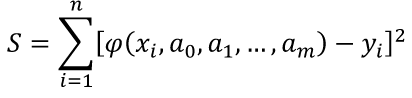 Коэффициенты a0, a1, …am надо определить из условий минимума функции: . Минимум функции найдем, приравнивая нулю частные производные по этим переменным: 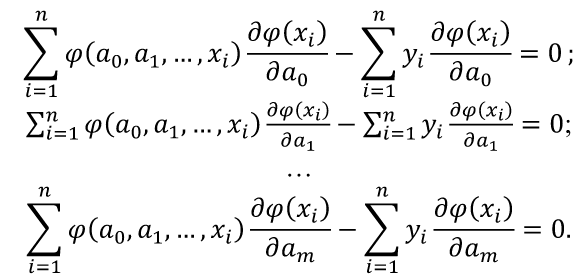 Данная система называется системой нормальных уравнений Для того чтобы найти коэффициенты, надо задать вид функции |
