Решение, получаемое численным методом, обычно
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
|
Линейная аппроксимация Зададим аппроксимирующую функцию как линейную: 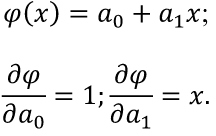 В итоге получаем формулу линейной аппроксимации: Квадратичная аппроксимация Зададим аппроксимирующую функцию в виде квадратного трехчлена: Мы получили систему линейных уравнений, поскольку в качестве аппроксимирующей функции выбрали многочлен. Если бы мы выбрали не многочлен, мы бы получили систему нелинейных уравнений. Теперь решим эту систему методом Крамера и найдем коэффициенты a0, a1, a2. Для удобства можно ввести обозначения: 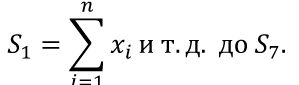 В этой системе все суммы (S1, … S7 ) являются константами, а все неизвестные – это коэффициенты a0, a1, a2. В итоге получим формулу квадратичной аппроксимации . ИНТЕРПОЛЯЦИЯ Одним из типов аппроксимации является интерполяция. Если коэффициенты ai функции определяются из условия равенства , т.е. функции совпадают в заданных известных точках, то такой способ аппроксимации называется интерполяцией или интерполированием. При этом точки Xi называют узлами интерполяции, а функцию – Интерполяционные кривые, которые строятся отдельно для разных частей заданного интервала изменения , называются кусочной или локальной интерполяцией. Если на всем интервале строится одна функция, то это глобальная интерполяция. В случае, если не возникает необходимости иметь коэффициенты многочлена, а надо, лишь найти значения функции в промежуточных точках, удобно использовать многочлен Лагранжа. Пусть в точках X0, X1...Xn заданы значения функции Y0, Y1… Yn. Необходимо найти значение функции в любой промежуточной точке . Многочлен Лагранжа имеет вид 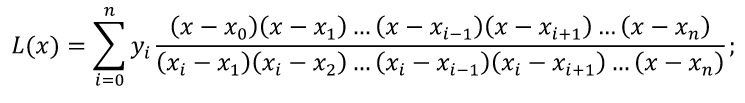 и будет искомым значением функции в точке X. Формулу (6.1) можно записать в общем виде 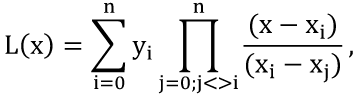 где – число точек (пары x, y). В итоге получим формулу Лагранжа. В эту формулу можно подставить любое значение , вычислить значение функции и сравнить его с исходными данными. Для повышения точности нужно увеличить количество узлов. Интерполяция методом Лагранжа Пусть в некоторых точках X0, X1...Xn известны значения функции f(x): y0, y1...Yn Необходимо определить величины функции f(x) при других значениях X. Связь y = f(x) неизвестна. Для решения этой задачи функцию f(x) требуется приближенно заменить свести решение (аппроксимировать) некоторой функцией f(X) так, чтобы отклонение в заданной области было наименьшим. На практике чаще всего применяется аппроксимация многочленами, т.е. Заметим, что при интерполировании m= n. Рассмотрим процесс интерполирования функций с помощью полиномов Лагранжа. Исходя из условия задачи, т.е. для 3 точек, имеем полином второго порядка (6.3): для которого, очевидно, должно выполняться: Формула (6.3) наглядно показывает, как получается полином любого порядка, но имеет больше теоретическое значение. Для практического же применения более удобна запись в форме (6.2), которая получается из (6.3), подставляя туда заданные числа X0, X1...Xn и Y0, Y1...Yn и выполняя очевидные преобразования. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ Во многих случаях, когда функция задана аналитически, определенный интеграл вычисляется по формуле Ньютона – Лейбница, которая состоит в том, что определенный интеграл равен приращению первообразной F(x) на отрезке интегрирования: Однако на практике не всегда можно вычислить интеграл с помощью этой формулы. Основными причинами являются: 1. Невозможность выразить первообразную функцию F(x) через элементарные функции. 2. Первообразная F(x) вычисляется через элементарную функцию, но выражение довольно сложное для вычисления. 3. Функция f(x) выражена таблицей. В случае, когда нельзя применить формулу Ньютона– Лейбница, обращаются к методам численного интегрирования. Методы численного интегрирования основаны на аппроксимации подынтегральной функции некоторыми более простыми выражениями, т.е. подынтегральную функцию f(x) заменяют другой приближенной функцией так, чтобы, во-первых, приближенная функция была близка к f(x) и, во вторых, интеграл от нее легко вычислялся. Формулы численного интегрирования называются квадратурами. Например, можно заменить подынтегральную функцию интерполяционным многочленом. К методам численного интегрирования относят такие методы как: метод прямоугольников (левых, правых, средних), трапеций, парабол (метод Симпсона). Рассмотри каждый из методов подробнее. Метод прямоугольников является одним из простейших методов. Данный метод использует замену определённого интеграла интегральной суммой. Формулу прямоугольников можно получить из геометрической интерпретации интеграла. Будем интерпретировать следующий интеграл: 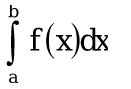 как площадь криволинейной трапеции, ограниченной графиком функции y = f(x), осью абсцисс и прямыми x = a и x = b . Разобьем отрезок [a,b] на равных частей длиной h так, что При этом получим точки (рис.7.1) 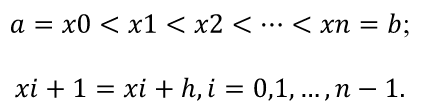 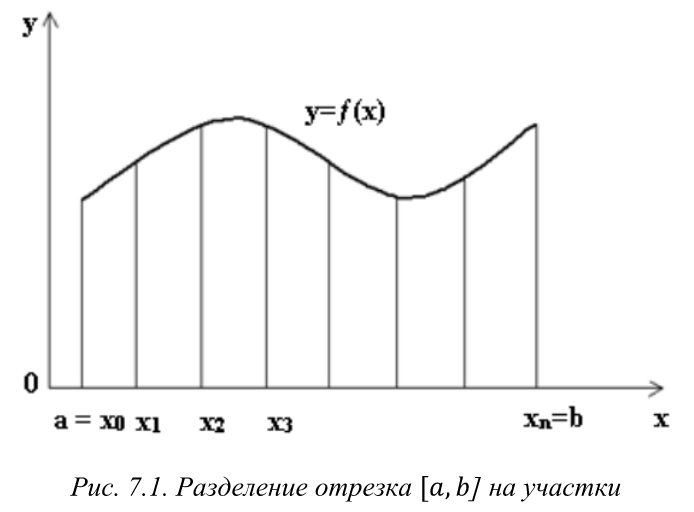 Заменим приближенно площадь криволинейной трапеции площадью ступенчатой фигуры, как показано на рис. 7.2. 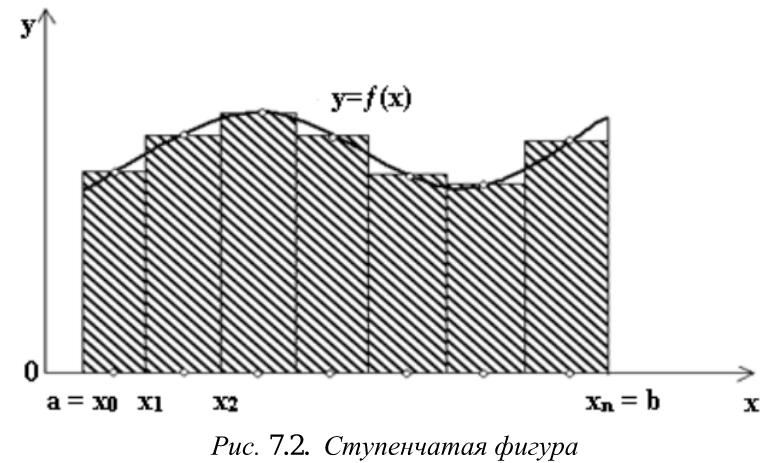 Более точной является формула прямоугольников, использующая функции в средних точках участков (рис.7.5 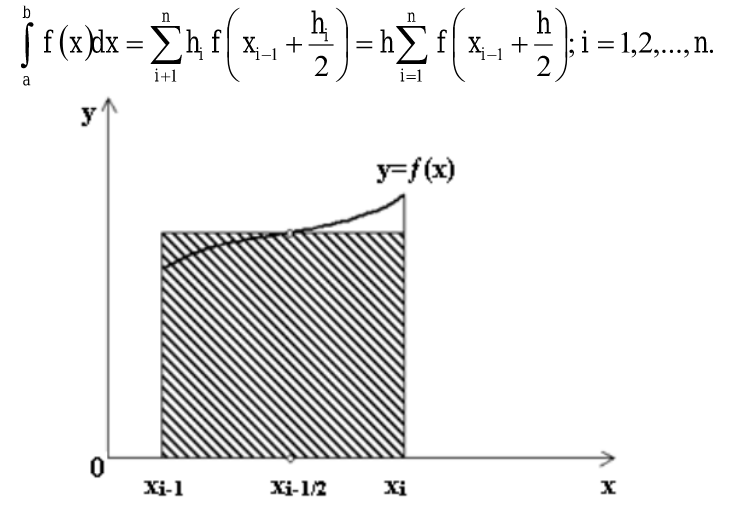 иллюстрация метод средних прямоугольников Метод трапеций Метод трапеций использует линейную интерполяцию, т.е. график функции y = f(x) представляется в виде ломаной, соединяющей точки (Xi, Yi) В этом случае площадь всей фигуры складывается из площадей элементарных трапеций (рис. 7.6): 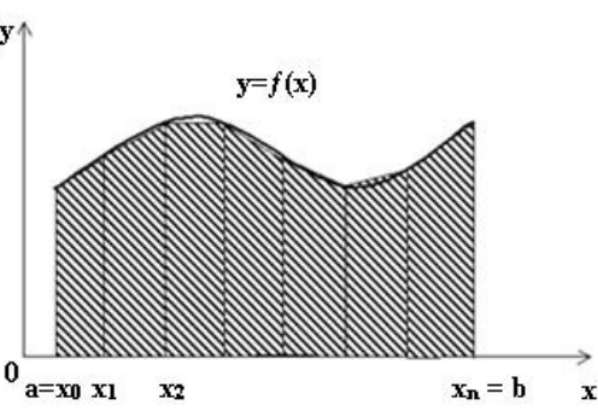 Рис. 7.6. Геометрическая интерпретация метода трапеций Площадь каждой такой трапеции равна произведению полусуммы оснований на высоту. Складывая эти равенства, получим следующую формулу для вычислений: 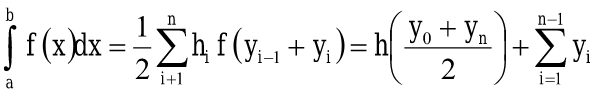 Точность интегрирования зависит от степени многочлена, количества участков и расположение точек. Во многих случаях формула средних прямоугольников дает лучшую точность, чем формула трапеций. Это на первый взгляд неожиданно, так как формула прямоугольников использует интерполяцию нулевого порядка, а формула трапеций – нелинейную. Здесь все дело в особом рассположении точек, которое повышает точность. Метод парабол (Симпсона) Метод парабол (Симпсона) подразумевает разбиение отрезка интегрирования [a, b], на четное число n равных частей с шагом h . На каждом отрезке подынтегральную функцию заменяют многочленом второй степени, т.е. уравнением квадратичной параболы. На каждом участке строится парабола, находится площадь фигуры, ограниченной полиномом 2–й степени и графиком подынтегральной функции. Далее находится сумма этих площадей. В результате получим следующую формулу для вычислений: 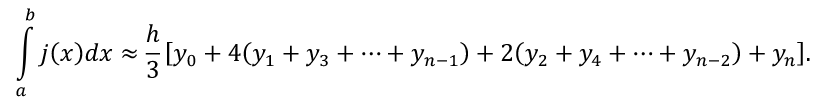 ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Решение дифференциальных уравнений является одной из важнейших математических задач. Обыкновенными дифференциальными уравнениями (ОДУ) называются уравнения, которые содержат одну или несколько производных от искомой функции Их можно записать в виде (8.1) где X – независимая переменная. Наивысший порядок n, входящей в уравнение производной, определяет порядок дифференциального уравнения. Уравнение первого порядка можн Решением дифференциального уравнения (8.1) называется всякая функция , которая после ее подстановки в уравнение превращает его в тождество. Общее решение ОДУ n–го порядка содержит N произвольных т.е. C1, C2… Cn. общее решение уравнения (8.1) имеет вид Частное решение ОДУ получается из общего, если произвольным постоянным придать определенные значения. Для уравнения первого порядка общее решение зависит от одной произвольной постоянной: . Если постоянная принимает определенное значение C = C0 , то получим частное решение: Чтобы выделить одно решение, задают начальное условие На рис. 8.1 представлено общее решение уравнения первого порядка – семейство интегральных кривых. Частным решением, согласно теореме Коши, является кривая, проходящая через точку C0. 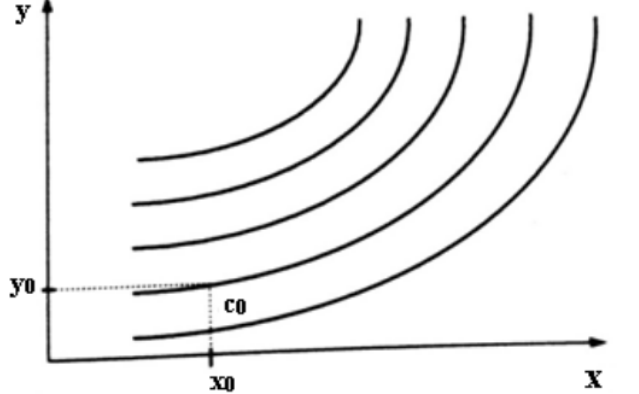 Рис. 8.1. Общее решение уравнения первого порядка – семей-ство интегральных кривых Рассмотрим теорему Коши. Если правая часть f(x, y) уравнения и ее частная производная определены и непрерывны в некоторой области G изменения переменных X, Y , то для всякой внутренней точки (X0, Y0) этой области данное уравнение имеет единственное решение, принимающее заданное значение y = y0 при x = x0 . |
