Решение, получаемое численным методом, обычно
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
|
8.1. Задача Коши Задача Коши заключается в отыскании функции y =y (x) , удовлетворяющей уравнению y’ = f(x, y) и начальному условию (8.2). Обычно определяют решение задачи Коши на отрезке, расположенном справа от начального значения [x0, xn] Наиболее распространенными численными методами решения дифференциальных уравнений являются методы конечных разностей Сущность этих методов состоит в том, что область непрерывного изменения аргумента и функции заменяется дискретным множеством точек, называемых узлами . Эти узлы составляют разностную сетку. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке. Эта функция называется сеточной. Исходное дифференциальное уравнение заменяется разностным уравнением, т.е. производные заменяются конечноразностными отношениями. Численными методами решаются не только отдельные уравнения, но и системы уравнений (чаще всего первого порядка), причем большинство методов решения одного уравнения легко распространяются на решение систем. 8.2. Метод Эйлера Метод Эйлера – наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Он имеет первый порядок точности. Метод реализуется следующим алгоритмом. Задано уравнение 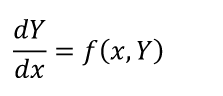 Отсюда получаем Зная значение функции в начальной точке , последовательно можно найти значения функции во всех точках сетки. Метод Рунге-Кутта Метод Рунге-Кутта является наиболее распространенным методом решения обыкновенных дифференциальных уравнений. Существует разностные схемы разного порядка точности, построенные на основе этого метода. Приведем метод четвертого порядка: 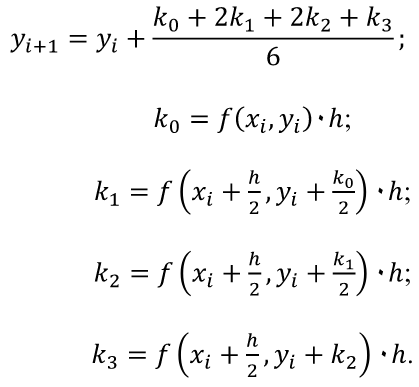 Данный метод требует на каждом шаге четырехкратного вычисления правой части уравнения, но это окупается повышенной точностью, что дает возможность производить расчет с более крупным шагом. Алгоритм расчета подобен алгоритму расчета Эйлера. Разница в том, что внутри цикла сначала вычисляются k0, k1, k2, k3 а затем – значение Y в новом расчетном узле. Приведем формулы Рунге–Кутта для системы двух уравнений: 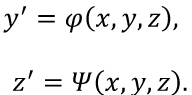 С начальными условиями при . Формулы имеют вид 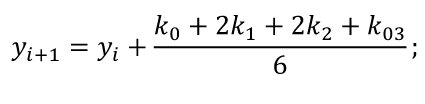 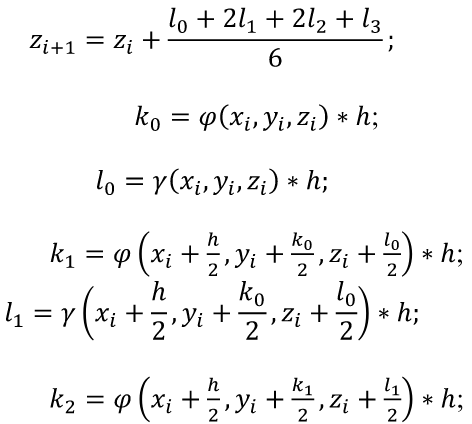 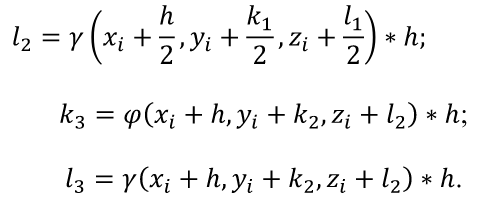 Аналогично можно записать формулы Рунге–Кутта для систем из трех и более уравнений. Алгоритм решения аналогичен алгоритму решения системы уравнений методом Эйлера. Сравнение методов решения дифференциального уравнения Сравним время решения ДУ по каждому из методов. Если мы уменьшим шаг в два раза, то, поскольку метод Рунге–Кутта имеет порядок точности погрешность уменьшится в 16 раз. Поскольку на каждом шаге правая часть уравнения вычисляется 4 раза, то количество вычислений увеличится в 8 раз. Чтобы уменьшить погрешность вычислений по методу Эйлера в 16 раз, необходимо уменьшить шаг в 16 раз, это значит, что в столько же раз увеличится количество вычислений правой части. Значит, для метода Рунге-Кутта потребуется в два раза меньше времени вычислений. Кроме того, при вычислении с шагом точность решения методом Рунге – Кутта была выше, а при уменьшении шага в большее число раз получим еще больший выигрыш по времени вычислений. Оба метода являются одношаговыми. Особенность таких методов состоит в том, что для получения решения в каждом новом расчетном узле достаточно иметь значение сеточной функции лишь в предыдущем узле. Это позволяет непосредственно начать счет при по известным начальным значениям, что допускает изменение шага в любой точке в процессе расчета. Недостатком одношаговых методов является трудность выбора шага. |
