Заказ 319865. Решение. Постоянная С
 Скачать 352.5 Kb.
|
|
Задача №1 Время Х (в тыс. часах) до выхода из строя авиационного двигателя, выработавшего гарантийный ресурс в 2 тыс. часов, является случайным с плотностью распределения: 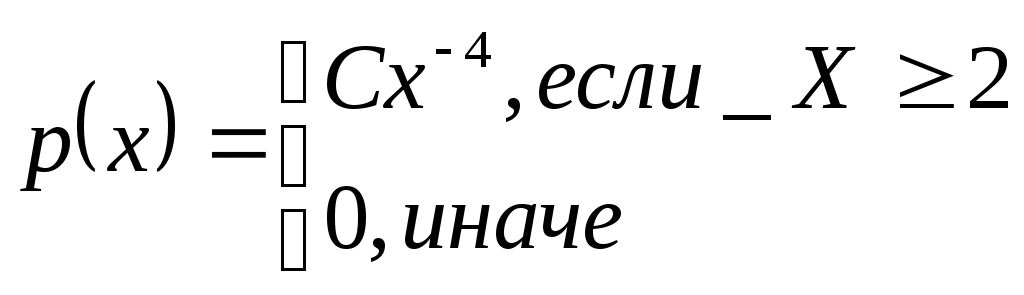 - Установить неизвестную постоянную С и построить график функции p(x) - Найти функцию распределения F(x) случайной величины и построить ее график - Вычислить математическое ожидание (среднее значение), дисперсию и среднее квадратическое (стандартное) отклонение рассматриваемой случайной величины - Во сколько раз число выходов из строя авиационных двигателей со временем работы после гарантийного срока меньше среднего превышает число выходов из строя авиационных двигателей после гарантийного срока выше среднего? Решение. Постоянная С 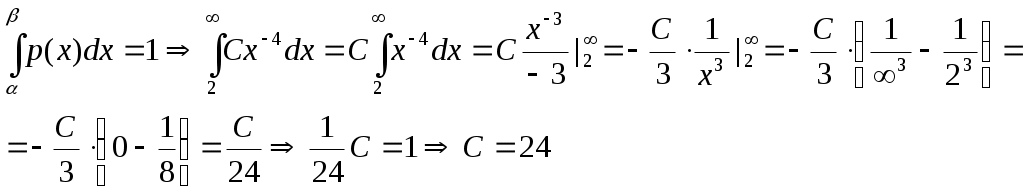 Тогда плотность распределения имеет вид 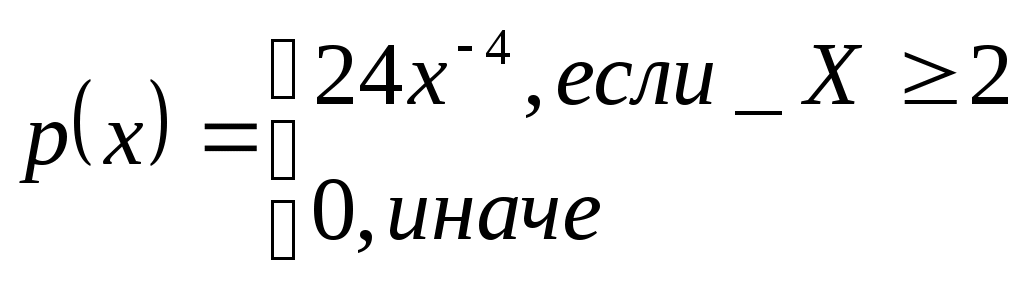 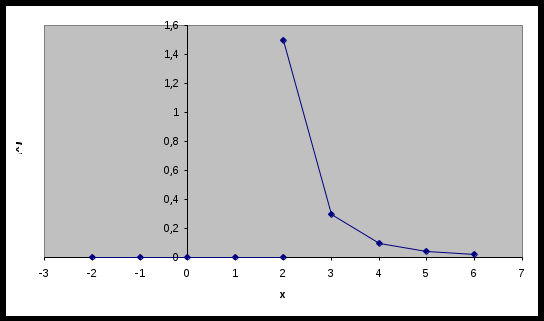 Рис. 1 Плотность распределения Функция распределения Т. к функция распределения изменяется от 0 до 1, она непрерывная и учитывая, что 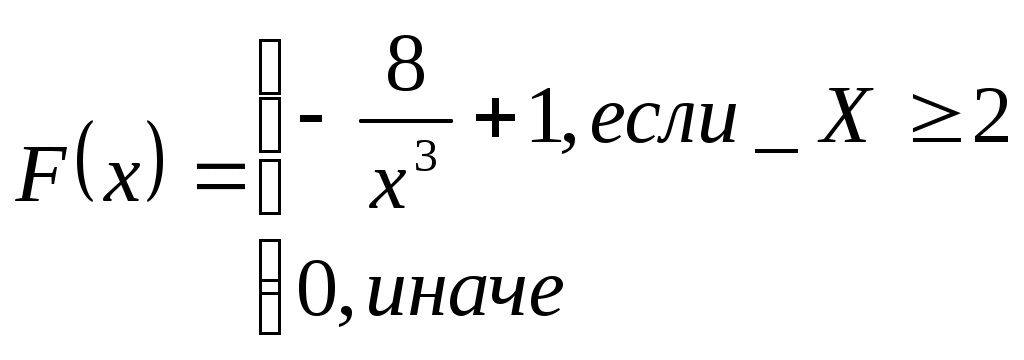 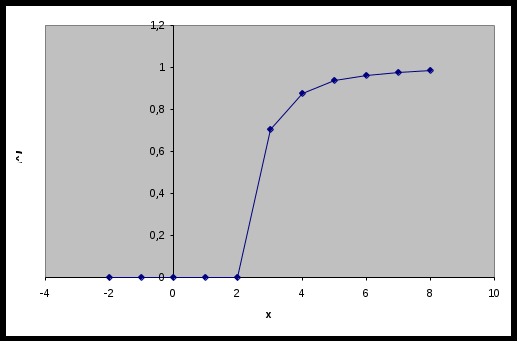, то имеем  Рис. 2 Функция распределения Математическое ожидание (среднее значение) 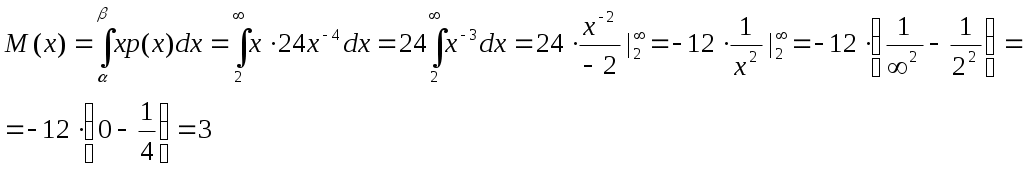 Дисперсия 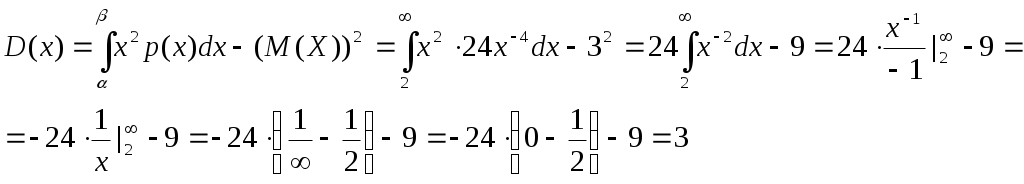 Среднее квадратическое (стандартное) отклонение  Вероятность того, что число выходов из строя авиационных двигателей со временем работы после гарантийного срока будет меньше среднего 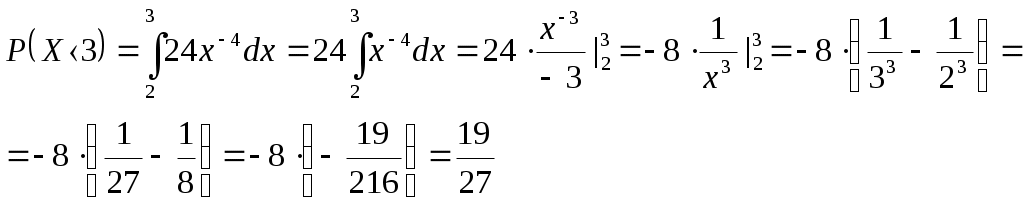 Вероятность того, что число выходов из строя авиационных двигателей со временем работы после гарантийного срока будет больше среднего 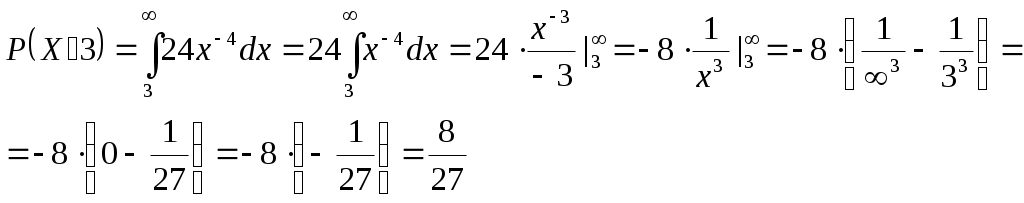 Т. о., число выходов из строя авиационных двигателей со временем работы после гарантийного срока меньше среднего число выходов из строя авиационных двигателей со временем работы после гарантийного срока выше среднего в (19/27):(8/27)=2,375 раза Задача №2 Студент знает 10 вопросов из 15. Экзаменатор задает ему 4 вопроса. Пятерка ставится за все правильные ответы, четверка – за три правильных ответа, тройка – за два правильных ответа, а в остальных случаях студент получает двойку. Составить ряд и функцию распределения для получаемой студентом на экзамене оценки и представить их графически. Решение. Случайная величина Х – оценка, получаемая студентом на экзамене, может принимать значения: 2, 3, 4, 5 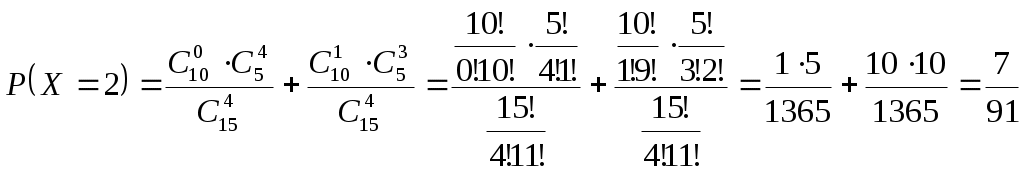 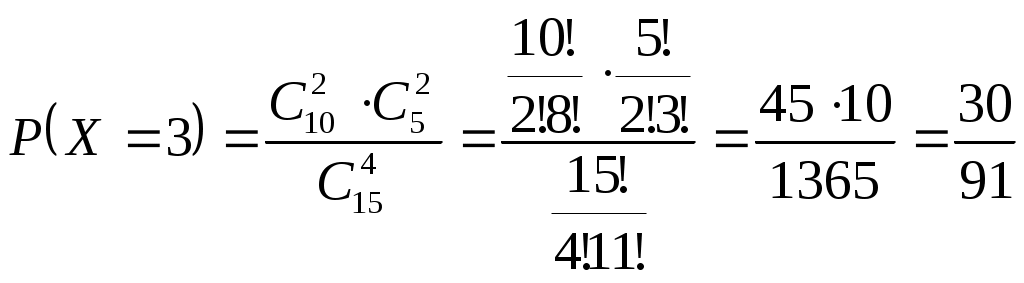 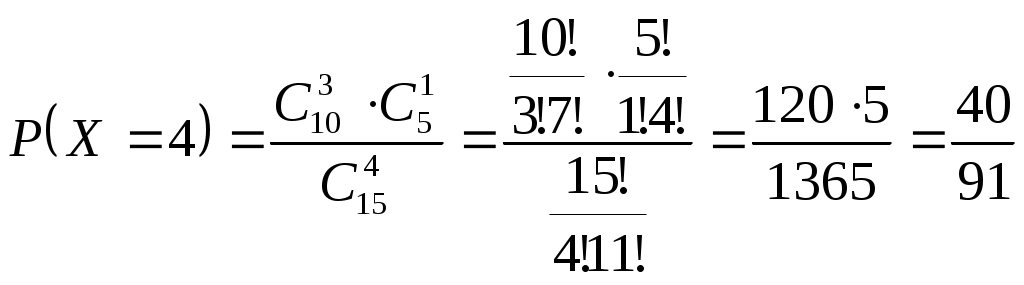 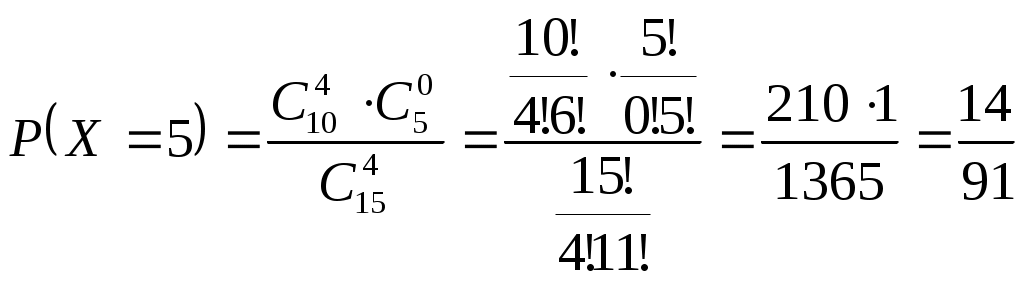 Получили ряд распределения Таблица 1. Ряд распределения
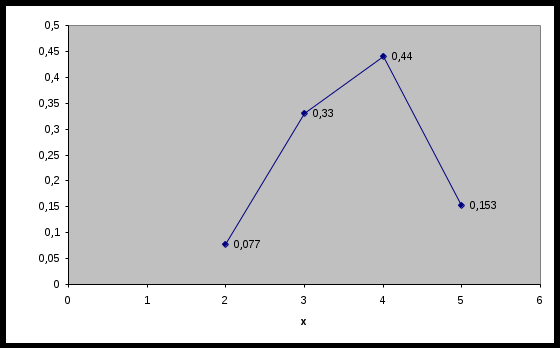 Рис. 1 Многоугольник распределения Функция распределения 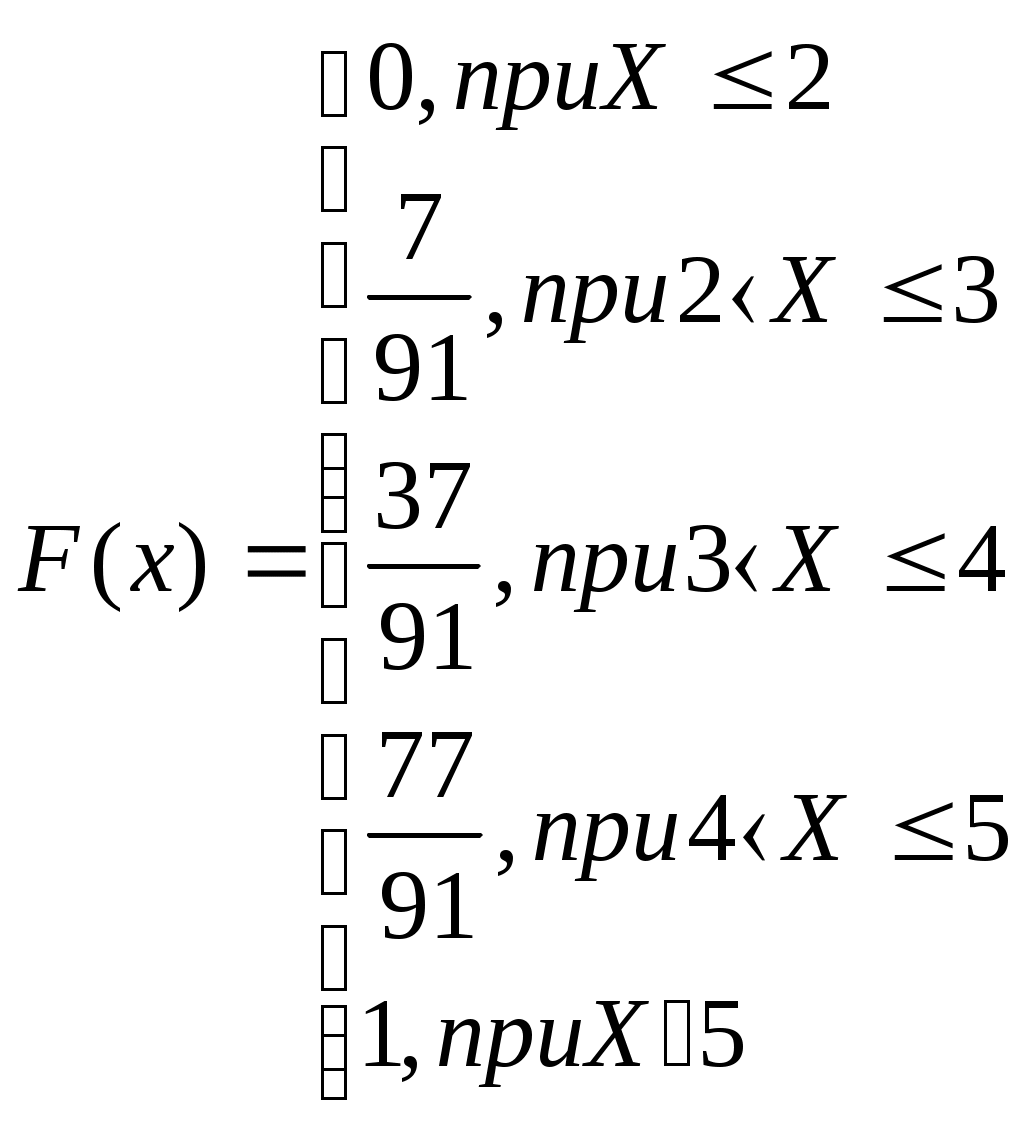 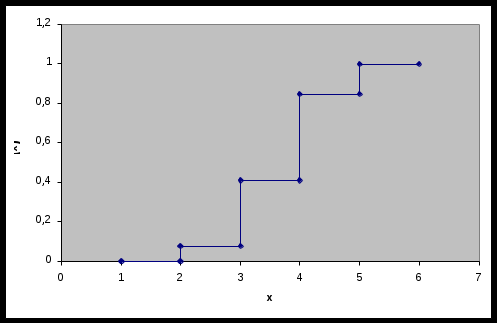 Рис. 2 Функция распределения Задача №3 При помощи дальномера произведено 25 измерений расстояния до некоторого объекта. Получены следующие результаты:
Необходимо: - Определить исследуемый признак и его тип (дискретный или непрерывный). - В зависимости от типа признака построить полигон или гистограмму относительных частот. - На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака. - Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение. - Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п. 3 закону распределения при уровне значимости 0,01. - Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,99. - С надежностью 0,99 проверить гипотезу о равенстве: а) генеральной средней значению 8; б) генеральной дисперсии значению 1,25 Решение. Представленный признак является непрерывным, т. к. имеет дробное выражение Сформируем интервальный ряд распределения, состоящий из 5 групп с равными интервалами Величина интервала  Таблица 1. Ряд распределения
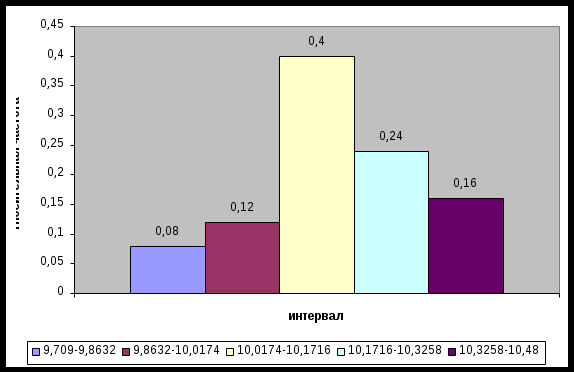 Рис. 1 Гистограмма распределения относительных частот На основе графического изображения необходимо выдвинуть гипотезу о нормальном распределении случайной величины Х Таблица 2. Расчет вспомогательных значений для определения средней и дисперсии
Среднее  Дисперсия 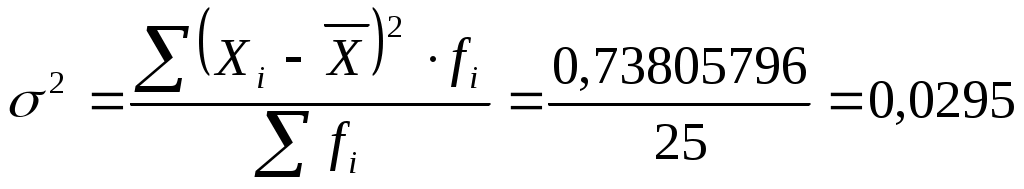 Среднее квадратическое (стандартное) отклонение  Проверка гипотезы о нормальном распределении Таблица 3. Расчет вспомогательных значений для оценки гипотезы о нормальном распределении
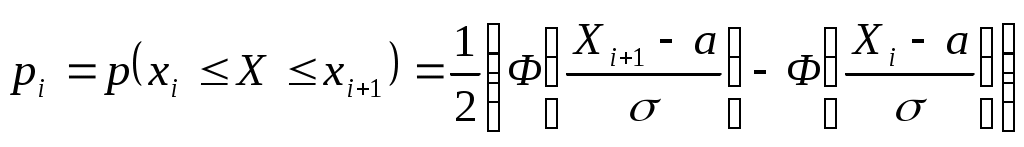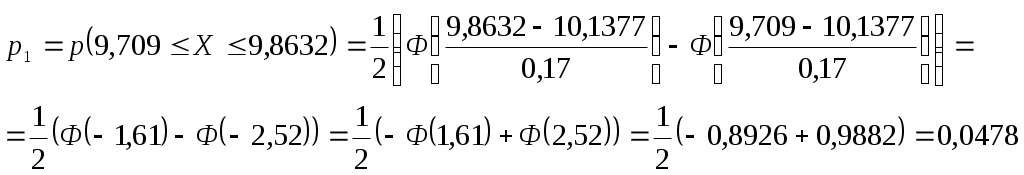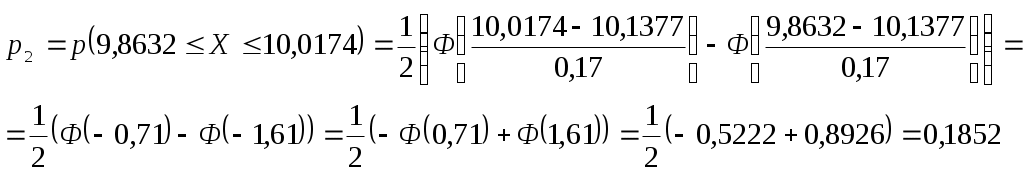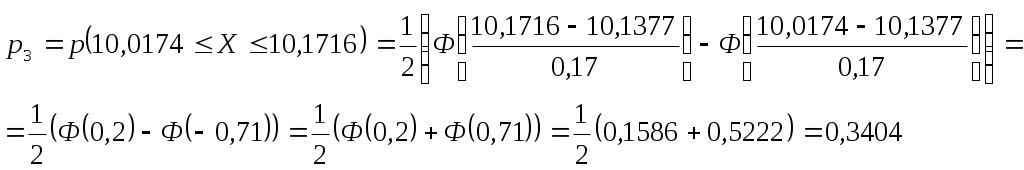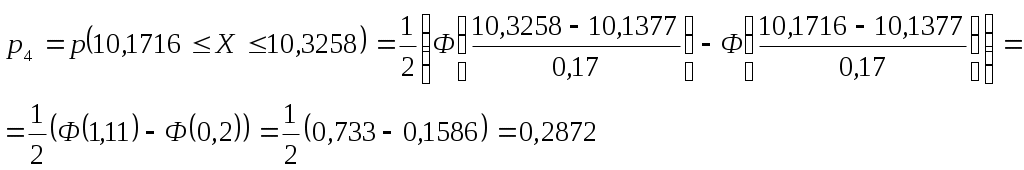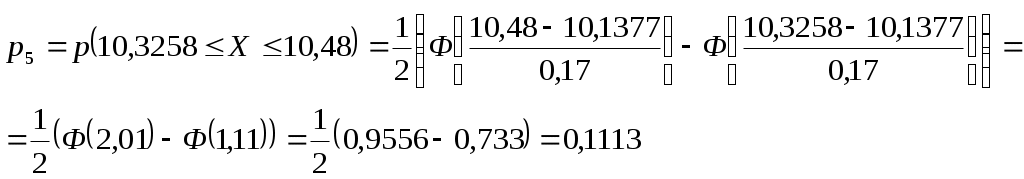        Т. к. 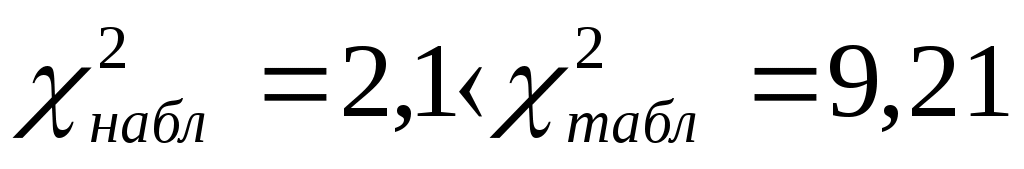 , то случайная величина Х распределена по нормальному законуДоверительный интервал для средней 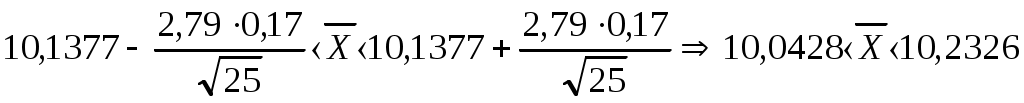   С доверительной вероятностью 0,99 среднее значение попадает в интервал от 10,0428 до 10,2326 Доверительный интервал для дисперсии 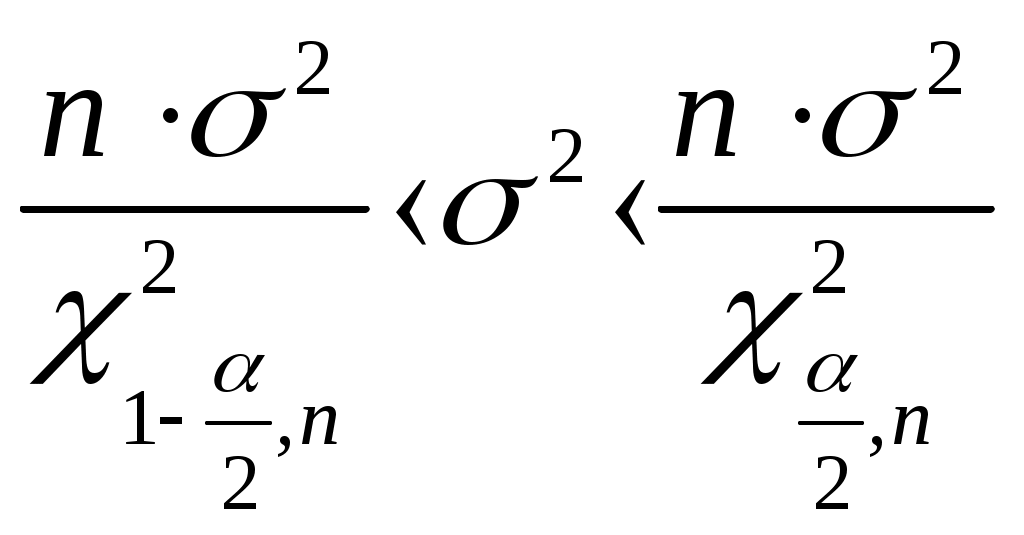 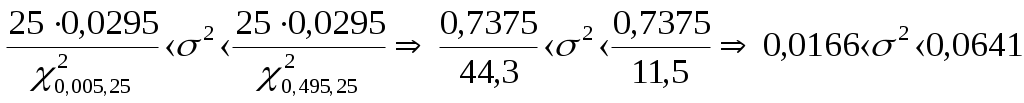 С доверительной вероятностью 0,99 дисперсия попадает в интервал от 0,0166 до 0,0641 Проверка с надежностью 0,99 гипотезы о равенстве генеральной средней значению 8 Выдвигаем гипотезу о равенстве генеральной средней значению 8, тогда 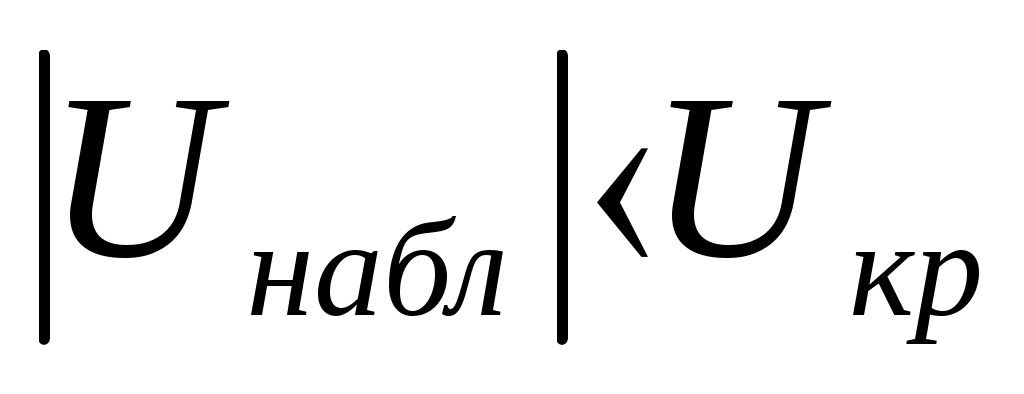   Т. к.  , то гипотеза о равенстве генеральной средней значению 8 отвергаетсяПроверка с надежностью 0,99 гипотезы о равенстве генеральной дисперсии значению 1,25 Выдвигаем гипотезу о равенстве генеральной дисперсии значению 1,25, тогда    Т. к. то гипотеза о равенстве генеральной дисперсии значению 1,25 принимаетсяЗадача № 4 В цехе с 10 станками ежедневно регистрировалось число вышедших из строя станков. Всего было проведено 200 наблюдений, результаты которых приведены ниже:
Необходимо: - Определить исследуемый признак и его тип (дискретный или непрерывный). - В зависимости от типа признака построить полигон или гистограмму относительных частот. - На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака. - Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение. - Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,99. - При уровне значимости 0,05 проверить гипотезу о том, что число выбывших из строя станков имеет распределение Пуассона. Решение. Представленный признак является дискретным, т. к. выражен конкретными целыми числами Таблица 1. Ряд распределения
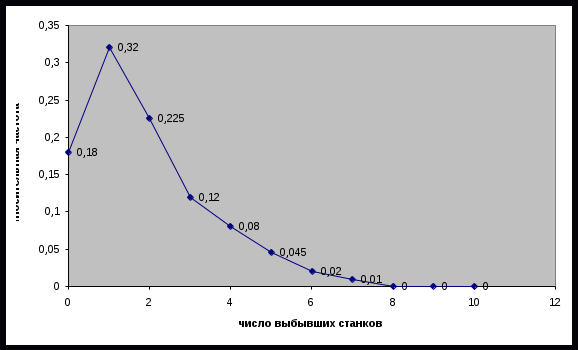 Рис. 1 Полигон распределения относительных частот На основе графического изображения необходимо выдвинуть гипотезу о распределении Пуассона случайной величины Х Таблица 2. Расчет вспомогательных значений для определения средней и дисперсии
Среднее  Дисперсия 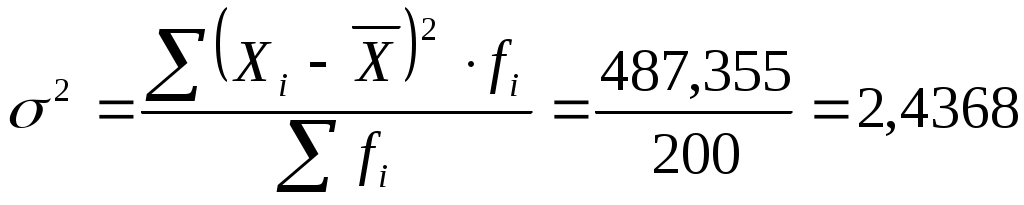 Среднее квадратическое (стандартное) отклонение  Доверительный интервал для средней 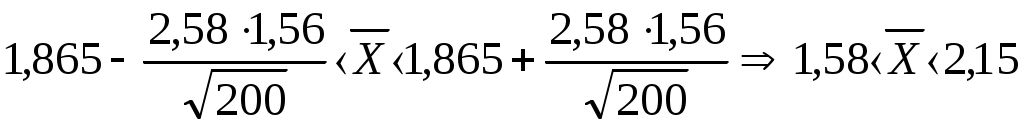  С доверительной вероятностью 0,99 среднее значение попадает в интервал от 1,58 до 2,15 Доверительный интервал для дисперсии 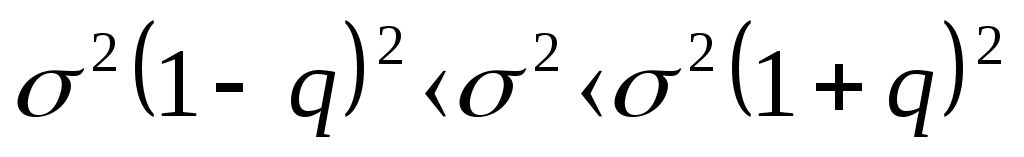 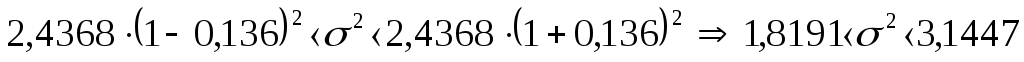  С доверительной вероятностью 0,99 дисперсия попадает в интервал от 1,8191 до 3,1447 Проверка гипотезы о распределении Пуассона случайной величины Х В качестве оценки параметра распределения Пуассона используем:  Закон Пуассона имеет вид:             Теоретические частоты             Таблица 3. Расчет вспомогательных значений для поверки гипотезы
  Т. к. 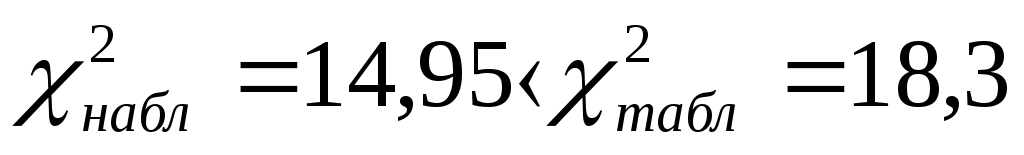 , то случайная величина Х распределена по закону ПуассонаБиблиографический список 1. Гулай, Т.А. Теория вероятностей и математическая статистика: учебное пособие / Т.А. Гулай, А.Ф. Долгополова, Д.Б. Литвин, С.В. Мелешко. - 2-е изд., доп. – Ставрополь: АГРУС, 2013. - 260 с.: - Режим доступа: http://znanium.com/bookread2.php?book=514780 2. Теория вероятностей и математическая статистика: Учебник / Е.С. Кочетков, С.О. Смерчинская, В.В. Соколов. - 2-e изд., испр. и перераб. - М.: Форум: НИЦ ИНФРА-М, 2014. - 240 с.: - Режим доступа: http://znanium.com/bookread2.php?book=447828 3. Высшая математика для экономистов: сборник задач: Учебное пособие / Г.И. Бобрик, Р.К. Гринцевичюс, В.И. Матвеев, Б.М. Рудык. - М.: НИЦ ИНФРА-М, 2015. - 539 с.: Режим доступа: http://znanium.com/bookread2.php?book=469738 |
