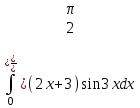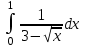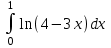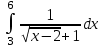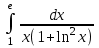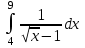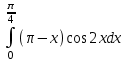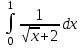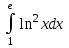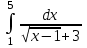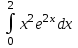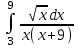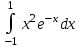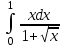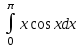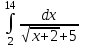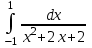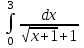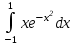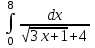Раздел 5 Интегрирование Практ занятие 2022. Решение Пример 2 Вычислите интеграл, используя таблицу интегралов Решение
 Скачать 308.43 Kb. Скачать 308.43 Kb.
|
|
РАЗДЕЛ 5. ПРАКТИЧЕСКОЕ ЗАДАНИЕ 3 ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Разбор типовых задач Пример 1 Вычислите интеграл, используя таблицу интегралов: 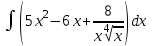 . .Решение. Пример 2 Вычислите интеграл, используя таблицу интегралов: 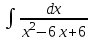 Решение.  Методы подстановки и подведения под знак дифференциала При применении метода подстановки (или замены переменной) 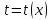 следует помнить, что нужно заменить и дифференциал согласно правилу: 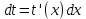 (*) (*)Замену переменной часто можно реализовать в виде техники подведения под знак дифференциала. При этом удобно использовать частные случаи формулы (*) и следствия из нее: 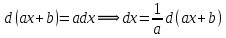 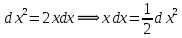 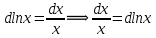 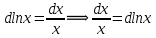 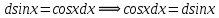 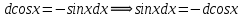 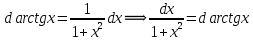 Пример 3 Вычислите интеграл: 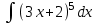 Решение. а) Используем замену переменной 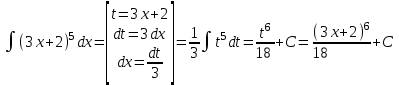 б) Используем технику подведения под знак дифференциала: 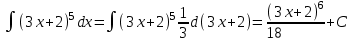 Пример 4 Вычислите интеграл, 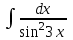 Решение. Используем технику подведения под знак дифференциала:   . .Пример 5 Вычислить интеграл: 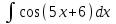 . .Решение. Используем технику подведения под знак дифференциала: Пример 6 Вычислите интеграл, используя технику подведения под знак дифференциала 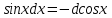 : :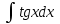 . .Решение. Пример 7 Вычислите интеграл: 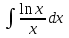 . .Решение. а) Используем замену переменной 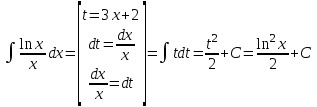 б) Используем технику подведения под знак дифференциала: 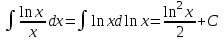 Пример 8 Вычислите интеграл, используя технику подведения под знак дифференциала: 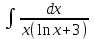 . .Решение. Используем технику подведения под знак дифференциала: 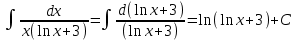 Пример 9 Вычислите интеграл: 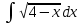 . .Решение. а) Используем замену переменной 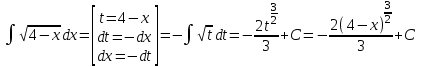 б) Используем технику подведения под знак дифференциала: 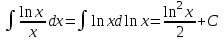 Пример 10 Вычислите интеграл, используя технику подведения под знак дифференциала: 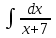 . .Решение. Используем технику подведения под знак дифференциала: 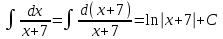 Пример 11 Вычислите интеграл, используя технику подведения под знак дифференциала: 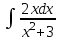 . .Решение. Используем технику подведения под знак дифференциала: 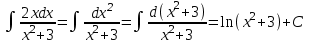 Пример 12 Найти неопределенный интеграл Решение. Используя линейные свойства интеграла, исходный интеграл заменяем линейной комбинацией интегралов: В последнем интеграле требуется предварительно выделить в знаменателе полный квадрат:   . .Используем таблицу интегралов и формулу Заметим, что нет необходимости после каждого интегрирования прибавлять произвольные постоянные, достаточно в конце прибавить одно итоговое слагаемое Используя формулу для дифференциала (*), получим формулу интегрирования: 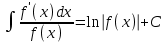 (**) (**)Пример 13 Вычислите интеграл: 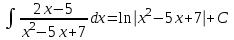 . .Решение. Заданный интеграл имеет вид (**), тогда 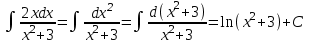 В некоторых интегралах замену переменных трудно свести к подведению под знак дифференциала. Пример 14 Вычислите интеграл, сделав замену переменной: 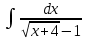 . .Решение. 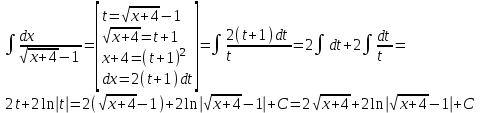 Интегрирование по частям или Применяя метод интегрирования по частям, следует придерживаться правилу: в качестве функции uнужно выбирать функцию, которая упрощается при дифференцировании. Тогда в интегралах вида: 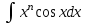 , , 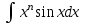 , , 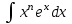 (n –целое) (n –целое) 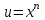 . .В интегралах вида: 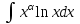 - - 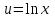 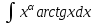 - - 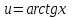 Пример 15 Вычислите интеграл, сделав замену переменной: 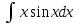 . .Решение.  Пример 16 Вычислите интеграл, сделав замену переменной: 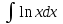 . .Решение.  Формула интегрирования по частям может применяться неоднократно. Пример 17 Вычислите интеграл, сделав замену переменной: 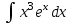 . .Решение. Интегрирование рациональных дробей методом неопределенных коэффициентов Рассмотрим метод неопределенных коэффициентов для дробей со знаменателем, который можно разложить на простые линейные множители. Пример 18 Вычислите интеграл: 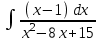 Решение. Разложим знаменатель на простые множители: 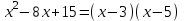 . .Тогда подынтегральная дробь может быть представлена в виде суммы дробей: 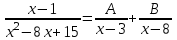 . .Неизвестные коэффициенты A и B находим из условия, что разложение является тождеством. Умножим дробь на общий знаменатель: 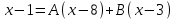 , ,1 способ. Общий метод. Раскроем скобки: 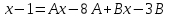 Поскольку это тождество, то должны быть равны коэффициенты при одинаковых степенях x в обеих частях тождества: 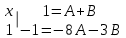 откуда 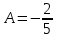 , , 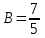 . . 2 способ. Метод частных значений. Поскольку это тождество, то возьмем два частных значения. Удобно взять корни знаменателя. 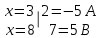 откуда 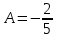 , , 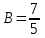 . . Тогда 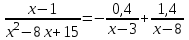 и 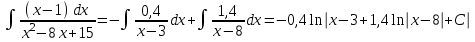 Интегрирование правильных рациональных дробей, знаменатель которых нельзя разложить на множители. Рассмотрим метод интегрирования правильных рациональных дробей, знаменателя которых нельзя разложить на множители. В этом случае в знаменателе выделяется полный квадрат и интеграл разлагается на сумму двух интегралов. Пример 19 Вычислите интеграл: 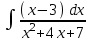 Решение. Выделим в знаменателе полный квадрат: 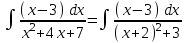 . .Сведем данный интеграл к сумме двух интегралов вида: 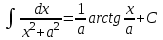 и 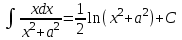 Для этого выделим в числителе выражение, полный квадрат которого выделен в знаменателе, и разложим интеграл на сумму двух интегралов: 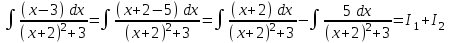 . .Рассмотрим каждый интеграл отдельно. В первом сделаем замену переменных: 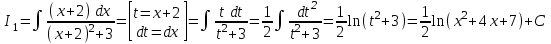 Второй интеграл сведем к табличному: 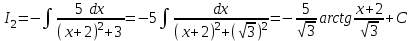 , ,В итоге: 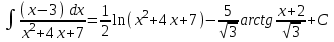 Пример 20 Вычислите определенный интеграл: 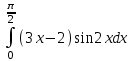 Решение. Применим метод интегрирования по частям 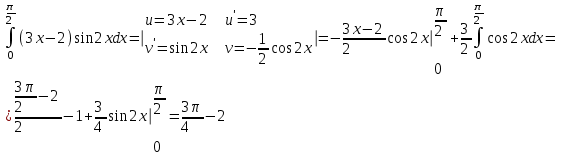 Пример 21 Вычислите определенный интеграл: 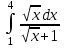 . .Решение. Применим метод замены переменной. При этом при вычислении определенного интеграла, в отличие от неопределенного, можно не возвращаться к исходным переменным, а заменить пределы интегрирования. 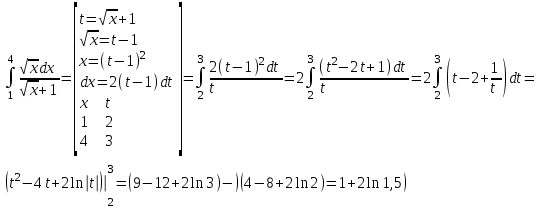 Пример 22 Вычислите площадь, ограниченную линиями: 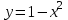 , , 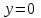 . .Решение. Фигура, площадь которой нужно определить изображена на рисунке. 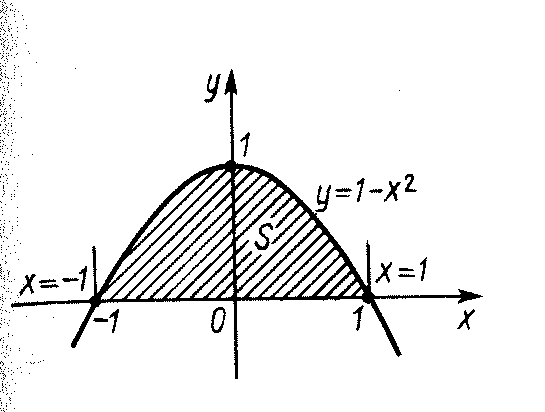 Тогда 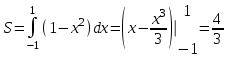 Пример 23 Вычислите площадь, ограниченную линиями: 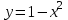 , , 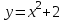 , , 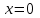 , , 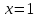 . .Решение. Фигура, площадь которой нужно определить изображена на рисунке. 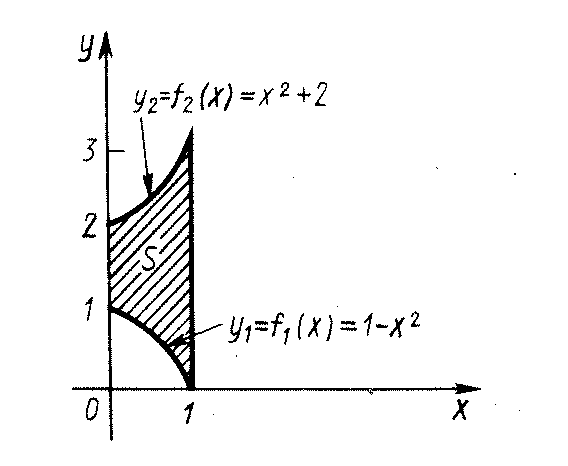 Тогда 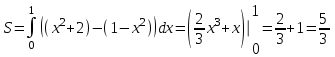 Задачи для самостоятельного решения Варианты задачи 1. Вычислите интегралы: а) 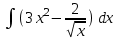 б) б) 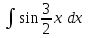 в) в) 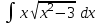 г) г) 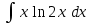 д) 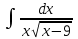 е) е) 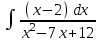 ж) ж) 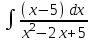 а) 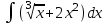 б) б) 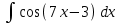 в) в) 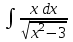 г) г) 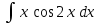 д) 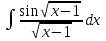 е) е) 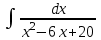 ж) ж) 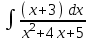 а) 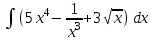 б) б) 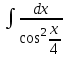 в) в) 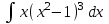 г) г) 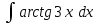 д) 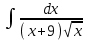 е) е) 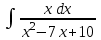 ж) ж) 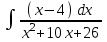 а) 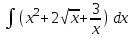 б) б) 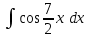 в) в) 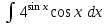 г) г) 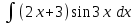 д) 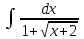 е) е) 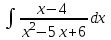 ж) ж) 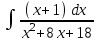 а) 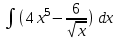 б) б) 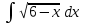 в) в) 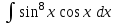 г) г) 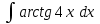 д) 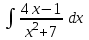 е) е) 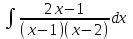 ж) ж) 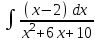 а) 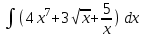 б) б) 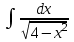 в) в) 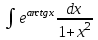 г) г) 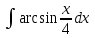 д) 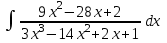 е) е) 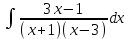 ж) ж) 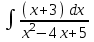 а) 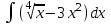 б) б) 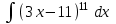 в) в) 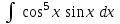 г) г) 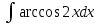 д) 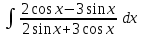 е) е) 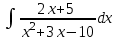 ж) ж) 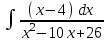 а) 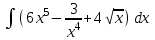 б) б) 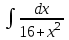 в) в) 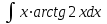 д) 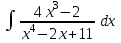 е) е) 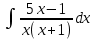 ж) ж) 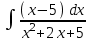 а) 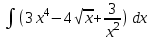 б) б) 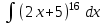 в) в) 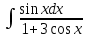 г) г) 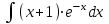 д) 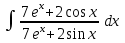 е) е) 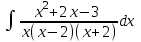 ж) ж) 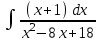 а) 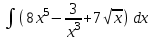 б) б) 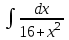 в) в) 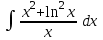 г) г) 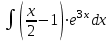 д) 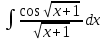 е) е) 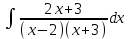 ж) ж) 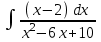 Варианты задачи 2. Вычислите определенные интегралы
Варианты задачи 3. Вычислите площадь фигуры. Вычислите площадь фигуры, ограниченной параболой Вычислите площадь, ограниченную линиями: Найдите площадь фигуры, ограниченной линиями 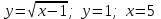 . .Найдите площадь фигуры, ограниченной линиями 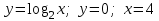 . .Найдите площадь фигуры, ограниченной линиями 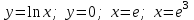 . .Найдите площадь фигуры, ограниченной линиями 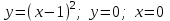 Найдите площадь фигуры, ограниченной линиями 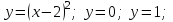 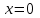 . .Найдите площадь фигуры, ограниченной линиями 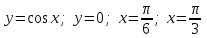 Найдите площадь фигуры, ограниченной линиями 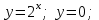 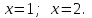 Найдите площадь фигуры, ограниченной линиями 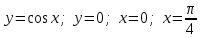 . .Варианты заданий в зависимости от номера в списке группы: В верхней строчке таблицы номер студента в списке группы, В ячейки на пересечении столбца с номером студента в списке группы со строчкой с номером задачи стоит номер варианта этой задачи. 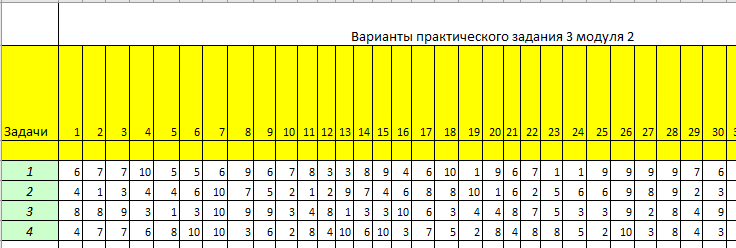 Требования к оформлению задания Предоставляется развернутое описание решения задач. Выполненное задание фотографируете, размещайте фотографии в ворд-файле с титульным листом. Указывайте номер задачи и номер варианта. |