ТВиМС. 520715 Теория вероятностей. Решение Рассчитаем вероятность выходя из строя ровно 1 конденсатора используя классическое определение вероятности

• Название: Решение Рассчитаем вероятность выходя из строя ровно 1 конденсатора используя классическое определение вероятности
• Анкор: ТВиМС
• Дата: 04.11.2022
• Размер: 177.51 Kb.
• Имя файла: 520715 Теория вероятностей.docx
• Тип: Решение; #770448
• страница: 2 из 4

-0,495

0,495


Рис. 8 – График функции Лапласа

2) В случае, если задано несмещенное значение среднеквадратического отклонения (s), вероятность покрытия математического ожидания интервалом рассчитывается согласно закону распределения Стьюдента со степенью свободы k=n-1. Тогда ошибка выборки будет рассчитываться по формуле:



По таблице Стьюдента найдем:



Тогда получим:



В этом случае с вероятностью 0,99 неизвестное математическое ожидание будет находиться в пределах:





8. По результатам эксперимента получена таблица наблюдений системы случайных величин (X, Y):

Y	X
	1	2	3	4	5	6
0,5	0,01	0,04	0,02	0,0	0,0	0,0
1,0	0,0	0,10	0,12	0,07	0,03	0,0
1,5	0,0	0,0	0,05	0,10	0,14	0,01
2,0	0,0	0,0	0,01	0,05	0,09	0,08
2,5	0,0	0,0	0,0	0,02	0,01	0,05

Оценить данную матрицу распределения (X, Y) на регрессию видов и .

Решение

Найдем одномерный закон распределения для Y по формуле:

	0,5	1,0	1,5	2,0	2,5
	0,07	0,32	0,3	0,23	0,08

Проверим:





Аналогично найдем одномерный закон распределения для Х (теперь суммы вероятностей будут рассчитываться по столбцам):















Закон распределения примет вид:

	1	2	3	4	5	6
	0,01	0,14	0,2	0,24	0,27	0,14

Дополним первоначальную таблицу построенными законами распределения.

Y	X
	1	2	3	4	5	6
0,5	0,01	0,04	0,02	0,0	0,0	0,0		0,07
1,0	0,0	0,10	0,12	0,07	0,03	0,0		0,32
1,5	0,0	0,0	0,05	0,10	0,14	0,01		0,3
2,0	0,0	0,0	0,01	0,05	0,09	0,08		0,23
2,5	0,0	0,0	0,0	0,02	0,01	0,05		0,08
	0,01	0,14	0,2	0,24	0,27	0,14		1

Построим условное математическое ожидание по формуле:















Тогда исходная таблица { } будет эквивалентна таблице { }:

	1	2	3	4	5	6
	0,5	0,857	1,125	1,72	1,648	2,143
	0,01	0,14	0,2	0,24	0,27	0,14

Вычислим оценки числовых характеристик системы (X,Y): математического ожидания, дисперсии, среднеквадратичного отклонения, ковариации, корреляционной матрицы, коэффициента корреляции и нормированной корреляционной матрицы: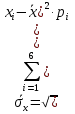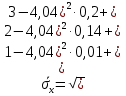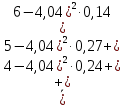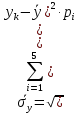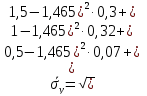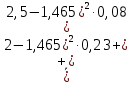































По формуле выполним линейную регрессию:





Так как коэффициент корреляции, характеризующий степень тесноты линейной зависимости между Y и Х, не очень близок к единице, оценим матрицу распределения системы случайных величин на линейную полиномиальную регрессию вида .

В данном случае с учетом постоянства дисперсии ошибок наблюдений полагаем: 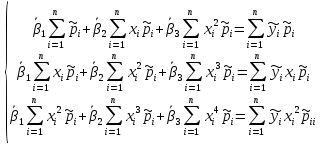в системе:



Вычислим коэффициенты системы, подсчитав предварительно суммы вида: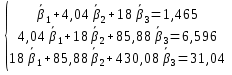





















Решим систему и получим:



Подставляя вычисленные суммы коэффициентами в систему и разрешая последнюю относительно , получим:



Построим графики 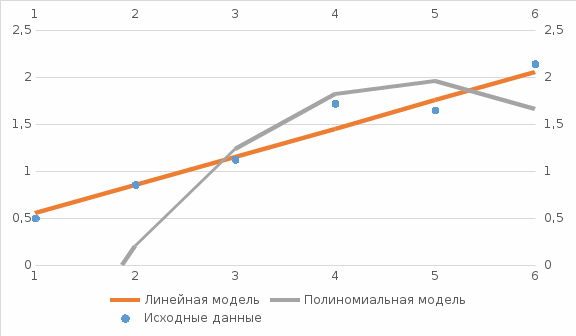и на фоне графически отображенной выборки (



Рис. 9 – График двумерного распределения

9. По двум независимым выборкам объемов n_X =11 и n_Y = 16 нормальных распределений найдены выборочные значениями математических ожиданий x = 30,5 и y = 29,0 и исправленные выборочные дисперсии