ТВиМС. 520715 Теория вероятностей. Решение Рассчитаем вероятность выходя из строя ровно 1 конденсатора используя классическое определение вероятности
 Скачать 177.51 Kb.
|
 = 0,8 и  = 0,6. При уровне значимости = 0.05 проверить нулевую гипотезу H0: mX = mY при конкурирующей H1: mX mY. Решение Так как заданные исправленные дисперсии различны, предварительно проверим гипотезу о равенстве дисперсий при помощи F-критерия Фишера: 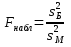  – значение большей исправленной выборочной дисперсии; – значение меньшей исправленной выборочной дисперсии. Исправленная дисперсия больше дисперсии , поэтому в качестве конкурирующей гипотезы примем гипотезу H: DX> DY. В этом случае критическая область – правосторонняя. По таблице критических точек распределения Фишера, по уровню значимости 0,05 и числам степеней свободы  и  находим критическую точку: Так как  , то гипотеза о равенстве дисперсий принимается.Предположение о равенстве дисперсий не отвергается, поэтому далее проверим гипотезу о равенстве математических ожиданий. Вычислим наблюдаемое значение критерия Стьюдента: 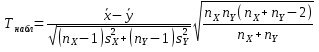 Подставим данные и получим:   По условию задачи конкурирующая гипотеза имеет вид: H1: mX mY, следовательно, критическая область является двусторонней. По таблице критических точек распределения Стьюдента, по уровню значимости = 0,05, помещенному в верхней строке таблицы, и числу степеней свободы  находим критическую точку: Так как  , то нулевую гипотезу о равенстве математических ожиданий отвергаем. То есть на уровне значимости = 0,05 математические ожидания различаются значимо.10. По критерию Пирсона при уровне значимости = 0.05 проверить гипотезу о распределении случайной величины Х по нормальному закону, если задано nk попаданий выборочных значений случайной величины Х в подинтервал k = (ak , bk):
Решение Определим объем заданной выборки по формуле:  Теперь рассчитаем значение математического ожидания:   - середина k-го интервала.
Подставим данные и получим:  Дисперсия предполагаемого нормального распределения случайной величины Х: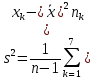 
 Подсчитаем вероятности pk для предполагаемого нормального распределения случайной величины Х по формуле:  где  и  – соответственно нижняя и верхняя границы подинтервалов k, причем крайние границы расширены до бесконечности (a1 =–, b7=), значения функции Лапласа Ф(х) вычисляются по таблице значений функции Лапласа.
|
