ТВиМС. 520715 Теория вероятностей. Решение Рассчитаем вероятность выходя из строя ровно 1 конденсатора используя классическое определение вероятности
 Скачать 177.51 Kb.
|
|
Вариант № 2 1. Из 100 конденсаторов за время Т из строя выходят 7 конденсаторов. Для контроля выбирают 5 конденсаторов. Найти вероятность того, что среди них за время Т из строя выйдет ровно 1 конденсатор, используя классическое определение вероятности, формулу Бернулли, формулу Пуассона и локальную теорему Лапласа. Решение Рассчитаем вероятность выходя из строя ровно 1 конденсатора используя классическое определение вероятности: 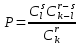 k – общее число конденсаторов; l – число конденсаторов, вышедших из строя; r – число выбранных для контроля конденсаторов; s – число дефектных конденсаторов в контрольной выборке. Подставим данные:  Определим вероятность заданного события по формуле Бернулли:  Рассчитаем вероятность появления вышедшего из строя конденсатора во всей выборке:  Тогда:  Подставим данные в формулу:  В случае, когда n велико, а p мало, применяют формулу Пуассона:  Рассчитаем параметр а:  Тогда получим:  Вероятность появления вышедшего из строя конденсатора по локальной теореме Лапласа:  где:  Рассчитаем:  По таблице Лапласа найдем:  Тогда получим вероятность появления вышедшего из строя конденсатора:  2. Система S состоит из трех независимых подсистем Sа, Sb и Sс. Неисправность хотя бы одной подсистемы ведет к неисправности всей системы (подсистемы соединены последовательно). Каждая подсистема состоит из двух независимых дублирующих блоков аk и bk (k = 1,2) (схема параллельного подсоединения блоков в подсистемах). 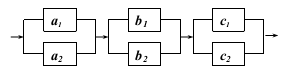 Найти надежность системы – вероятность того, что система будет исправна в течение некоторого времени, если известны надежности блоков P(аk) = 0,8, P(bk) = 0,9, P(сk) = 0,7. Решение Введем обозначения: Аk – событие, состоящее в том, что блок аk исправен; Bk – событие, состоящее в том, что блок bk исправен; Ck – событие, состоящее в том, что блок ck исправен; S – событие, состоящее в том, что система исправна; Sа – событие, состоящее в том, что подсистема а исправна; Sb – событие, состоящее в том, что подсистема b исправна; Sc – событие, состоящее в том, что подсистема c исправна. Разобьем систему на три подсистемы: а, b и с. Подсистема а дублирующих блоков исправна в том случае, когда исправен хотя бы один из блоков аk (k = 1,2), т. е.:  – сумма двух совместных независимых событий. Следовательно:   Аналогично проведем расчеты и для остальных двух систем. Для системы В:    Для системы С:    Так как для исправности всей системы необходима исправность подсистем a, b и с, то получим:  Подставим данные:  Надежность системы составляет 86,49%. 3. Испытывается прибор, состоящий из двух узлов а и b, соединенных последовательно в смысле надежности. Надежности (вероятности безотказной работы за время Т) узлов а и b известны и равны P(а) =0,8, P(b) = 0,9. Узлы отказывают независимо друг от друга. По истечении времени Т выяснилось, что прибор неисправен. Найти с учетом этого вероятность того, что неисправен только узел а. Решение Вероятность выхода из строя прибора, если неисправен только узел а:  Вероятность выхода из строя прибора, если неисправен только узелb:  Тогда вероятность того, что неисправен только узел а:  То есть вероятность того, что прибор выйдет из строя из-за неисправности узла а составляет 0,346. 4. Из партии, содержащей 100 изделий, среди которых имеется 20 дефектных, выбраны случайным образом 5 изделий для проверки их качества. Для случайного числа Х дефектных изделий, содержащихся в выборке, построить ряд распределений, функцию распределения и их график, найти ее числовые характеристики. Решение Так как максимальное количество дефектных изделий равно 5, то возможные значения х будут равны: x=0,1,2,3,4,5. Вероятность того, что в заданной выборке окажется ровно k дефектных изделий, составит: 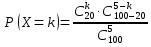 Подставим каждое значение х и рассчитаем вероятность каждого из них с точностью 0,0001: 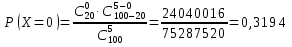 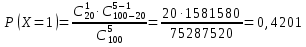  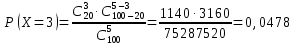 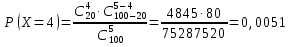  Используем для проверки правильности расчетов равенство:   Расчет вероятностей проведен верно. Закон распределения случайной величины дефектных изделий примет вид:
Составим функцию распределения F(  ) случайной величины .Если  , то  Если  , то  Если  , то  Если  , то  Если  , то Если  , то  Если  , то  Функция F(Z) будет иметь вид:  Графически функция будет иметь вид: 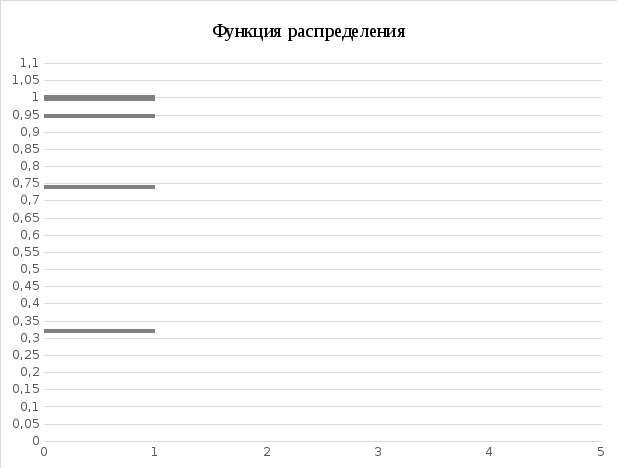 Рис. 1 – График функции распределения Найдем числовые характеристики случайной величины X . Математическое ожидание:   Дисперсия:    Среднее квадратическое отклонение:  5. Задана плотность распределения f(х) случайной величины Х:  Требуется найти коэффициент А, построить график плотности распределения f(х), найти функцию распределения F(х) и построить ее график, найти вероятность попадания величины Х на участок от 0 до 0,25. Найти числовые характеристики случайной величины Х. Решение Для определения коэффициента А воспользуемся свойством плотности распределения:  Тогда получим:  График плотности f(x) представим на рисунке:   1 -1 0,75 Рис. 2 – График плотности распределения f(х) По формуле:  получим выражение функции распределения: График функции F(х) изобразим на рисунке: 1 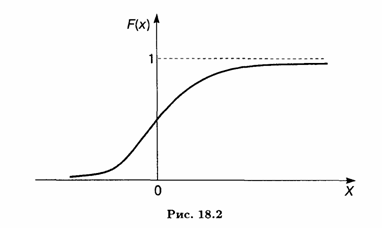 -1 Рис. 3 – График функции распределения По формуле  находим вероятность попадания величины Х на участок от 0 до 0,25: 6. По выборке объема n = 100 построен ряд распределения:
Построить гистограмму, полигон и эмпирическую функцию распределения. Найти точечные оценки математического ожидания, дисперсии, среднеквадратичного отклонения, асимметрии и эксцесса. Решение Гистограмма относительных частот представляется в виде примыкающих друг к другу прямоугольников с основаниями, равными интервалу между значениями:  Рис. 4 – Гистограмма частот 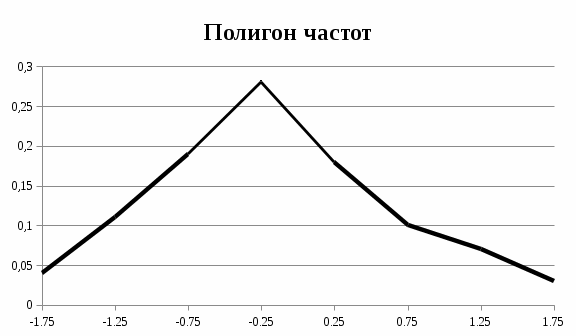 Рис. 5 – Полигон частот Составим функцию распределения F( ) случайной величины .Если  , то  Если  , то  Если  , то  Если  , то  Если  , то Если  , то Если  , то  Если  , то  Если  , то Функция F(Z) будет иметь вид: 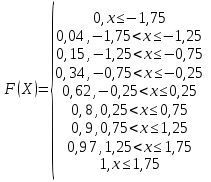 График функции распределения примет вид: 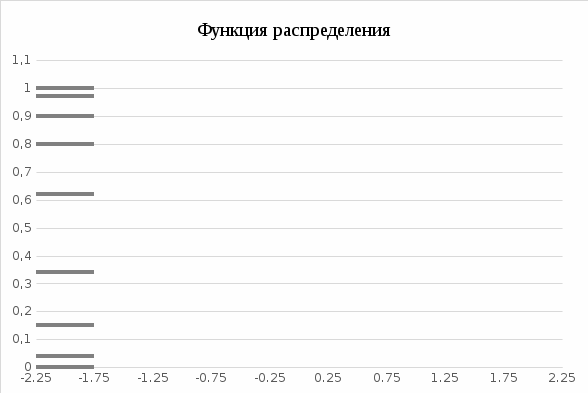 Рис. 6 – График функции распределения Оценкой математического ожидания случайной величины X служит выборочное среднее взвешенное:  Оценкой дисперсии случайной величины X служат выборочная дисперсия и модифицированная выборочная дисперсия, вычисляемые по формулам:  Составим вспомогательную таблицу.
   Оценка среднеквадратического отклонения представляет собой корень из дисперсии:  Это значит, что значения выборки отличаются от среднего значения не более чем на 3,237. Коэффициенты асимметрии (скошенности) и эксцесса (островершинности) рассчитаем по формулам:  Определим центральные моменты 3-го и четвертого порядков: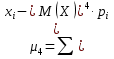  
    Так как величина показателя асимметрии положительна, следовательно, речь идёт о правосторонней асимметрии. Показатель эксцесса меньше нуля, то есть заданное распределение плосковершинное. 7. Найти доверительный интервал с надежностью = 0.99 неизвестного математического ожидания нормальной случайной величины Х, зная x = 20,9, n = 26, если 1) = 2, 2) s = 2. Решение В данном случае имеем:  Воспользуемся таблице для функции Лапласа и найдем значение t:  1) Рассчитаем ошибку выборки по формуле:  Все данные известны, подставим их в формулу и получим:  Тогда с вероятностью 0,99 неизвестное математическое ожидание будет находиться в пределах:   На рисунке 7 затемненной областью на фоне графика плотности нормального распределения выделена площадь, численно равная β. На рисунке 8 на фоне графика Лапласа выделена точка (t, Ф(t)).   Рис. 7 – График плотности нормального распределения    |
