Контрольная по сопромату реакции и сечения. Вариант 3. Решение Рисунок Расчетная схема Реакции опор и определим из уравнений статики, (1), (3)
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
|
Задача 1. 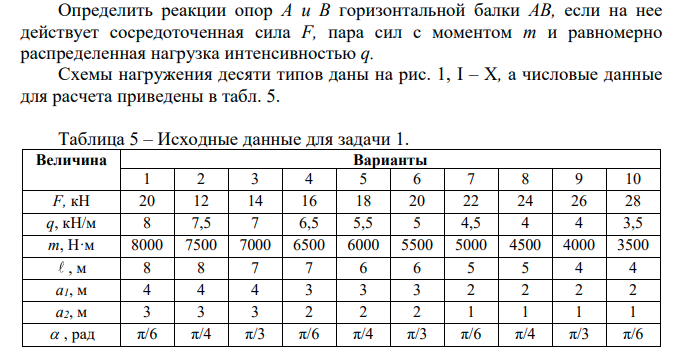 Исходные данные: F = 14 кН, q = 7 кН/м, m = 7000 Н∙м = 7 кН∙м, l = 7 м, a1 = 4 м, a2 = 3 м, α = π/3 рад. Решение: 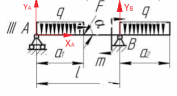 Рисунок – Расчетная схема Реакции опор 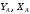 и и 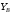 определим из уравнений статики: определим из уравнений статики: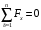 , , 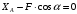 ; (1) ; (1)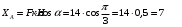 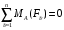 , , 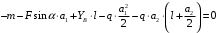 ; (3) ; (3)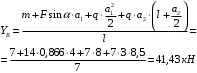 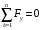 , , 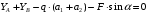 ; (2) ; (2)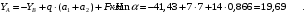 Значения реакций опор положительные, направления показаны верно. Выполним проверку, составив уравнение моментов относительно т. В: 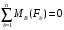 , , 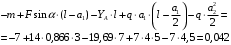 ; (3) ; (3)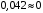 , реакции опор определены правильно. , реакции опор определены правильно.Задача 2. 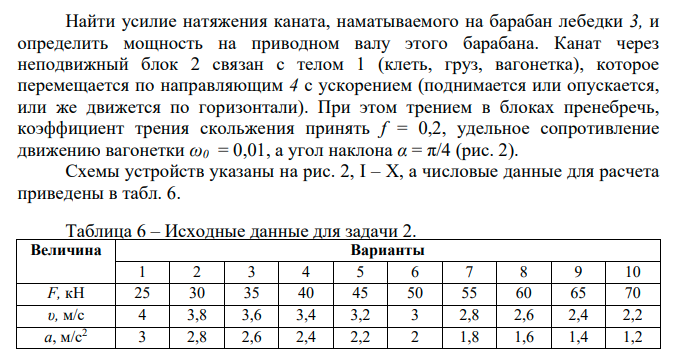 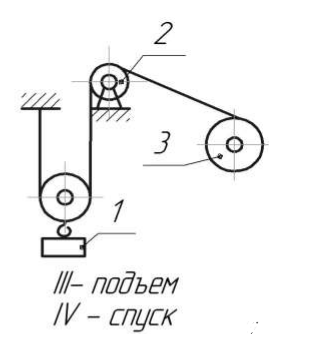 Задача 3. Стальной стержень переменного сечения находится под действием продольной силы Р и собственного веса. Найти наибольшее напряжение в сечении круглого бруса и определить величину перемещения сечения 1 — 1. 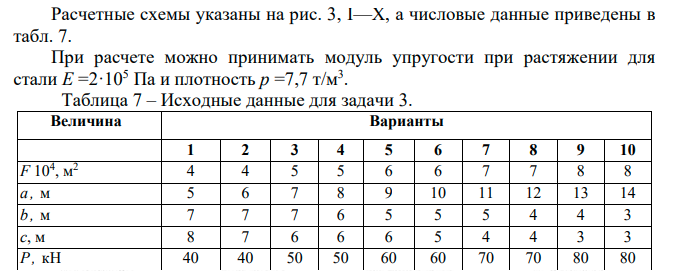 Исходные данные: F = 5∙10-4 м2, а = 7 м, b = 7 м, с = 6 м, Р = 50 кН. 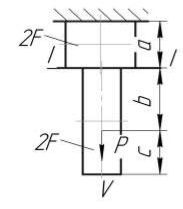 Практическая работа №1 Определить равнодействующую системы сходящихся сил геометрическим и аналитическим способами. Определить погрешность вычислений двумя способами. Исходные данные: F1= 18 кН, F2= 10 кН, F3= 16 кН, F4= 4 кН, F5= 15 кН, α1 = 60°, α2 = 30°, α3 = 170°, α4 = 230°, α5 = 210°. Решение: 1. Определение равнодействующей геометрическим способом. Используя свойства векторной суммы сил, вычерчиваем векторы сил в масштабе 2 мм = 1 кН последовательно друг за другом. Равнодействующей вектор соединяет начало первого вектора с концом последнего и направлен ему навстречу. С помощью линейки определяем модуль равнодействующей силы, а транспортира угол наклона к её оси. Fсум = 18,72 кН, αсум = 137°. 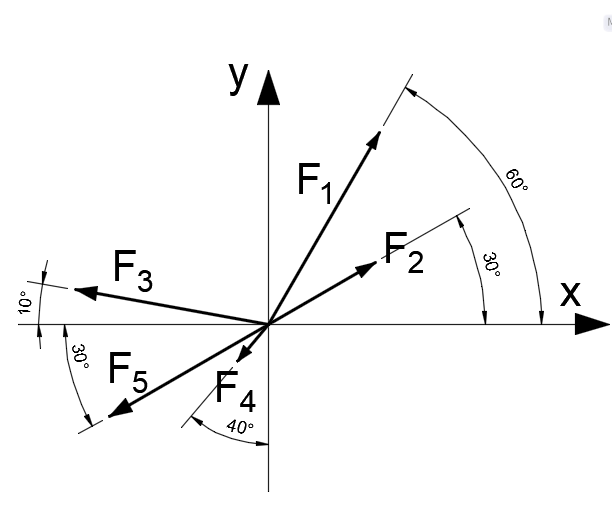 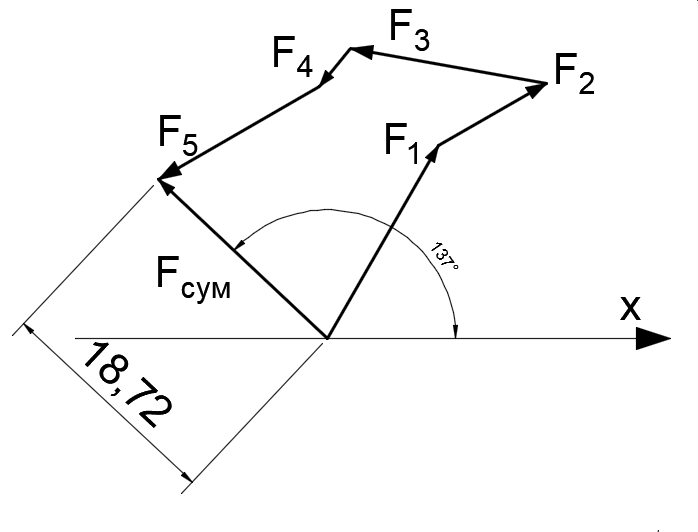 2. Определение равнодействующей аналитическим способом: а) Определяем проекции всех сил системы на ось Ох: F1х= F1· соs 60° = 18 ·0,5 = 9 кН F2х= F2 · соs 30° = 10 · 0,866 = 8,66 кН F3х= – F3 · соs 10° = – 16 · 0,985 = –15,76 кН F4х= – F4 · соs 50° = – 4 · 0,643 = – 2,572 кН F5х= – F5 · соs 30° = – 15 · 0,866 = – 12,99 кН Сложив алгебраические проекции, получим проекцию равнодействующей на ось Ох: FΣх = F1х + F2х + F3х + F4х + F5х; FΣх = 9 + 8,66 – 15,76 – 2,572 – 12,99 = – 13,662 кН. Знак – проекции соответствует направлению влево. б) Определяем проекции всех сил системы на ось Оу: F1у= F1 · соs 30° = 18 · 0,866 = 15,588 кН F2у= F2 · соs 60° = 10 · 0,5 = 5 кН F3у= F3 · соs 80° = 16 · 0,174 = 2,784 кН F4у= – F4 · соs 40° = – 4 · 0,766 = – 3,06 кН F5у= – F5 · соs 60° = – 15 · 0,5 = – 7,5 кН Сложив алгебраические проекции, получим проекцию равнодействующей на ось Оу: FΣу = F1у + F2у + F3у + F4у + F5у; FΣу = 15,588 + 5 + 2,784 – 3,06 – 7,5 = 12,812 кН. Знак + проекции соответствует направлению вверх. в) Определяем модуль равнодействующей по величине проекции: 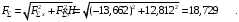 г) Определяем значение угла равнодействующей с осью Ох: 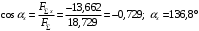 3. Определение погрешности вычислений. 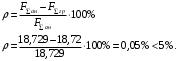 Вывод: равнодействующая определена правильно. Практическая работа №2 Задание 1. Определить величины реакций в заделке. Провести проверку правильности решения. Исходные данные: F1 = 5 кН, F2 = 15 кН, g = 2 кН/м, m = 70 кН∙м, схема 3. 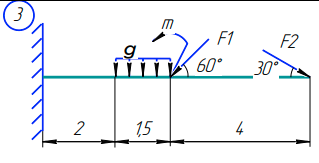 Решение: Заменяем распределенную нагрузку сосредоточенной 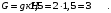 Освобождаем балку АВ от связей, отбрасываем заделку в точке А и заменяем действие заделки возможными реакциями, возникающими в опоре – 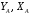 и реактивным моментом и реактивным моментом 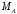 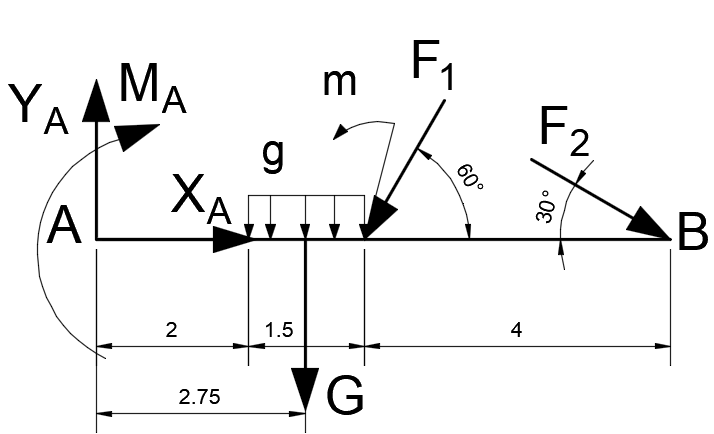 Реакции опор 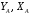 и и 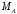 определим из уравнений статики: определим из уравнений статики: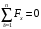 , , 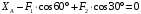 ; (1) ; (1)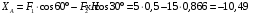 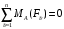 , , 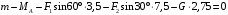 ; (3) ; (3)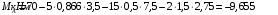 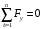 , , 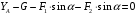 ; (2) ; (2)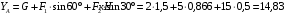 Если значения реакций опор отрицательные, то направления противоположны указанным. Выполним проверку, составив уравнение моментов относительно т. В: 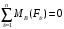 , , 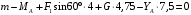 ; ;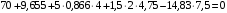 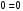 , реакции опор определены правильно. , реакции опор определены правильно.Задание 2. Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения. Исходные данные: F1 = 15 кН, F2 = 25 кН, g = 5 кН/м, m = 40 кН∙м, схема 4. 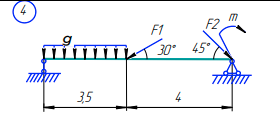 Решение: Заменяем распределенную нагрузку сосредоточенной 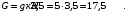 Освобождаем балку АВ от связей, отбрасываем заделку в точке А и заменяем действие заделки возможными реакциями, возникающими в опорах – 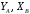 и и 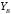 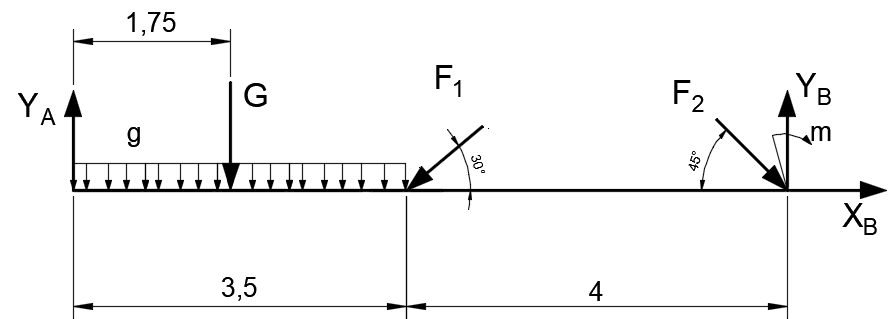 Реакции опор 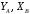 и и 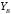 определим из уравнений статики: определим из уравнений статики: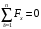 , , 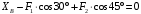 ; (1) ; (1)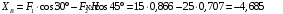 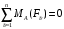 , ,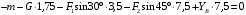 ; (3) ; (3)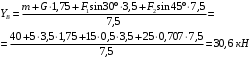 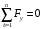 , , 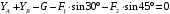 ; (2) ; (2)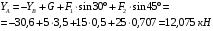 Если значения реакций опор отрицательные, то направления противоположны указанным. Выполним проверку, составив уравнение моментов относительно т. В: 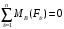 , , 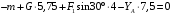 ; ;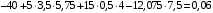 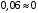 , реакции опор определены правильно. , реакции опор определены правильно.Практическая работа №3 Задание 1. Определить координаты заданного сечения. Порядок выполнения работы: 1) Разбить фигуру на простые геометрические фигуры, положение центров тяжести которых известны. 2) Выбрать систему координат. 3) Определить площади геометрических фигур. 4) Определить центр тяжести каждой фигуры относительно координат х, у. 5) Определить общую площадь фигуры по формуле А= ΣАi. 6) Определить координаты центра тяжести всей фигуры. Исходные данные: 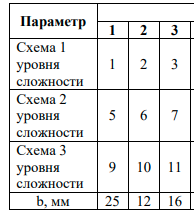 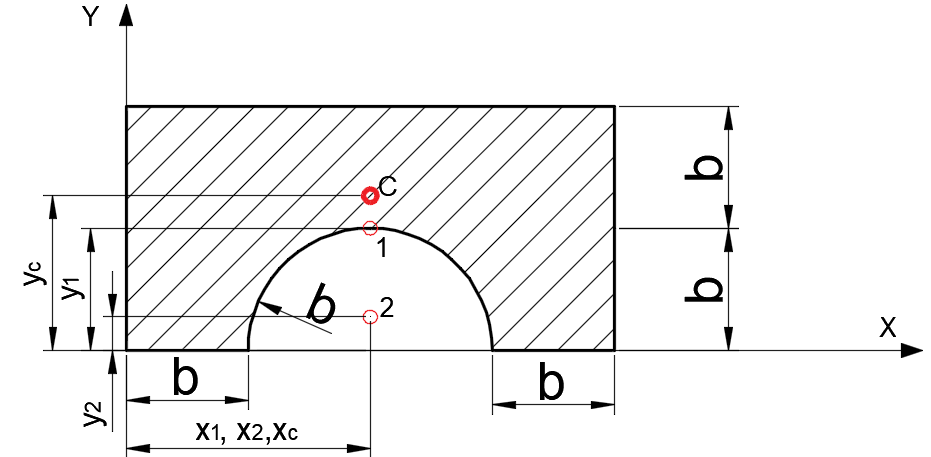 Решение: 1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны. Представляем фигуру в виде прямоугольника 1 и выреза 2 в виде полукруга. 2. Вычисляем площадь и координаты центра тяжести каждого элемента: 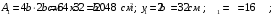 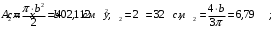 Площадь выреза берем со знаком минус. 3. Площадь фигуры 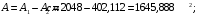 4. Находим координаты центра тяжести всей фигуры: 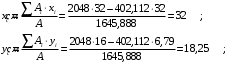 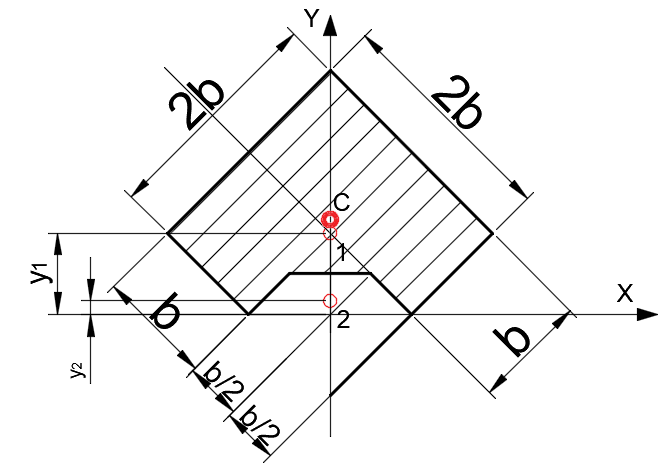 1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны. Представляем фигуру в виде квадрата 1 и выреза 2 в виде трапеции. 2. Вычисляем площадь и координаты центра тяжести каждого элемента: 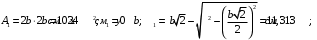 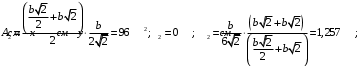 Площадь выреза берем со знаком минус. 3. Площадь фигуры 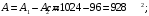 4. Находим координаты центра тяжести всей фигуры: 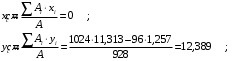 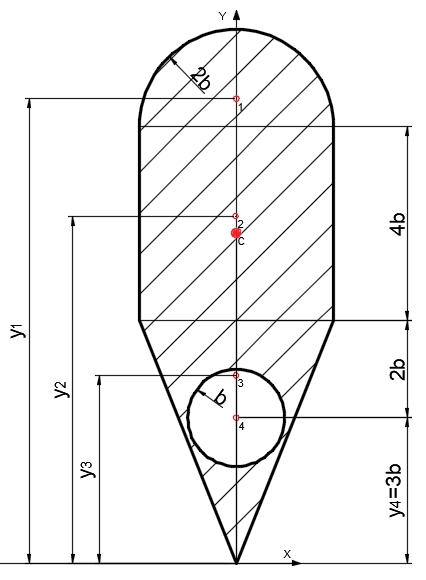 1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны. Представляем фигуру в виде полукруга 1, прямоугольника 2, равнобедренного треугольника 3 и выреза 4 в виде круга. 2. Вычисляем площадь и координаты центра тяжести каждого элемента: 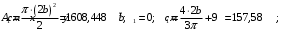 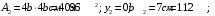 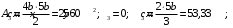 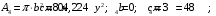 Площадь выреза берем со знаком минус. 3. Площадь фигуры 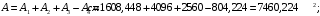 4. Находим координаты центра тяжести всей фигуры: 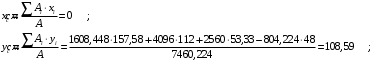 Задание 2 Определить координаты центра тяжести сечения, составленного из профилей проката, как показано на рисунке ниже. Сечение состоит из двутавровой балки № 22, двух уголков 80×50×6 мм. 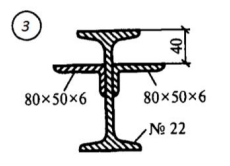 1. Разобьем сечение в соответствии с профилями проката и обозначим их 1, 2, 3. 2. Укажем центры тяжести каждого профиля и обозначим их С1, С2, С3. 3. Выберем систему осей координат. Ось у совместим с осью симметрии, а ось х направим перпендикулярно оси у и проведем через центр тяжести двутавровой балки. 4. Выпишем формулы для определения координат центра тяжести сечения: хс=0, так как ось у совпадает с осью симметрии; 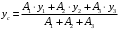 Учитывая, что А2 = А3, а также, что у2 = у3, получим: 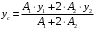 5.Определим площади и координаты центров тяжести отдельных профилей проката 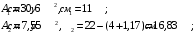 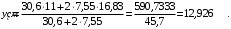 Укажем положение центра тяжести сечения С на схеме. 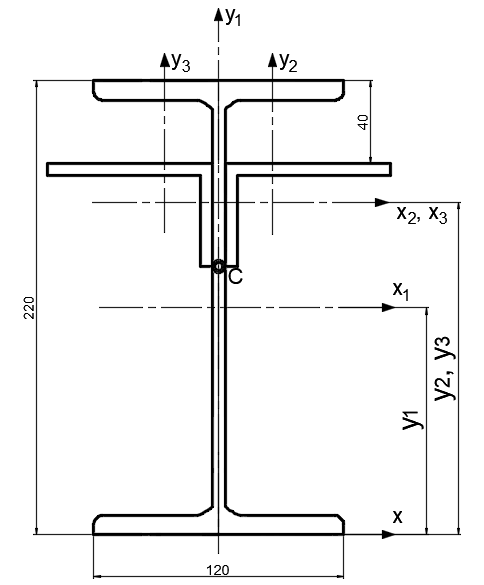 |
