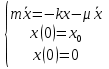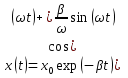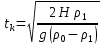Решение Рисунок Условные обозначения
 Скачать 0.6 Mb.
|
|
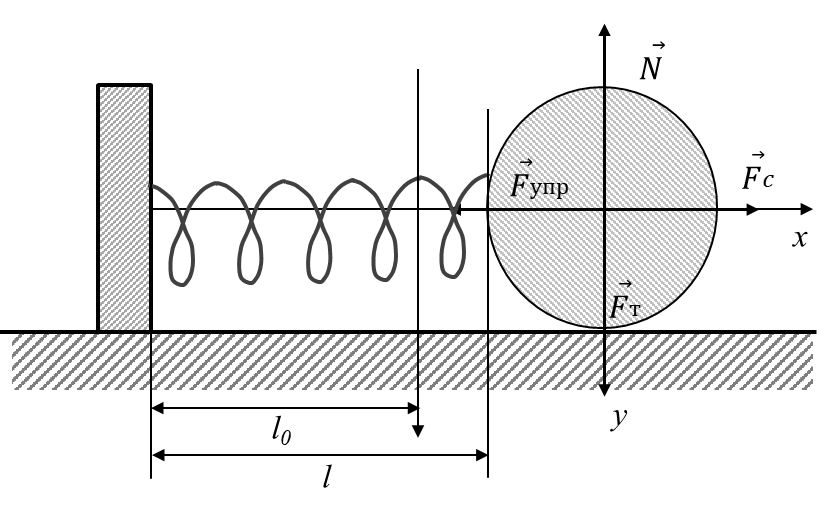
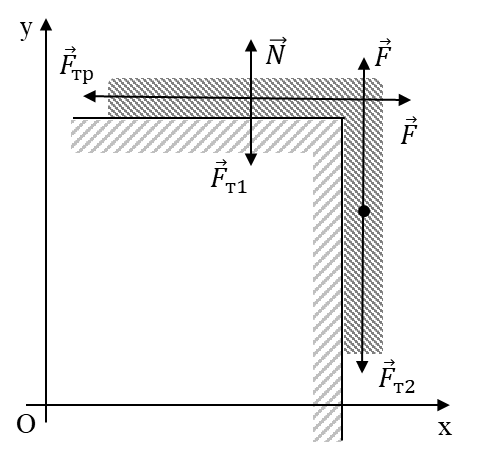
Задание 1. Построить математическую модель механической системы, состоящей из пружины с жесткостью k, один конец которой жестко закреплен, а на другом находится тело массой m. Тело скользит по горизонтальному стержню: коэффициент трения скольжения μ. Смещение тела из положения равновесия равно x0. Найти: а) амплитуду, частоту и период свободных колебаний механической системы; б) частоту и период затухающих колебаний системы; в) уравнение огибающей кривой колебаний; г) смещение, скорость и ускорение тела в момент времени t для затухающих колебаний. Построить графики смещения свободных и затухающих колебаний системы в зависимости от времени. k = 94 н/м , m = 0,6 кг , μ = 0,52 , x0 = 10 см , t = 2,5 с. Решение:
Пусть l0 и l – длина пружины до и после деформации соответственно. Тогда х = l – l0 – абсолютная деформация пружины или величина отклонения положения равновесия. При этом на тело действуют следующие силы: 1) сила упругости пружины:  , где  – коэффициент жесткости пружины.2) сила трения:  , где  – коэффициент сопротивления; – скорость;3)  – реакция опоры;4) сила тяжести груза:  ,где m – масса тела;  – ускорение свободного падения.По второму закону Ньютона:   Проекция на ось y:  так как движение вдоль оси y отсутствует, то N = mg. Проекция на ось х:   .Обозначим через х = х(t) – величину отклонения тела от положения равновесия в производный момент времени t. Выразим через х ускорение и скорость:   Таким образом,  Добавив начальные условия:  – начальное смещение; – начальная скорость.построим математическую модель рассматриваемой системы в виде задачи Коши для ОДУ второго порядка (1):
Преобразуем уравнение (1), перенесём все слагаемые в левую часть и разделим на m:  Введем обозначения:    Получим уравнение (2):
Решаем уравнение (2) для начальных условий задачи:
При отсутствии сопротивления среды μ = 0 уравнение (2) принимает вид (5):
которое описывает свободные колебания механической системы. а) Решая дифференциальное уравнение (5) с условиями (3), (4), получим (6):
Выражение (6) представляет собой гармонические колебания (синусоидальную зависимость) с круговой частотой ω0 и амплитудой x0. Подставляя численные значения исходных данных, получим: - амплитуда свободных колебаний системы x0 = 0,1 м; - частота свободных колебаний механической системы:   - период свободных колебаний механической системы:   График смещений свободных колебаний системы 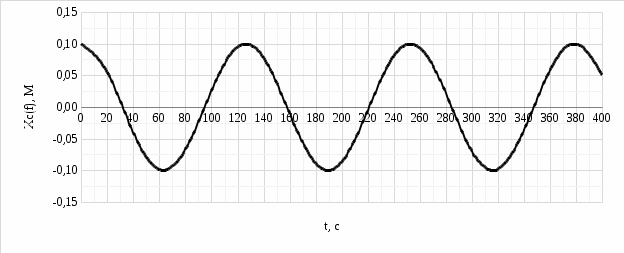 представлен на рисунке 2. Рисунок 2. График смещений свободных колебаний системы б) Решая дифференциальное уравнение (2) с условиями (3) и (4), получим (7):
где 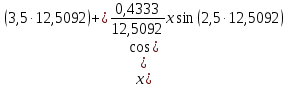 .  х - частота затухающих колебаний системы:   - период затухающих колебаний механической системы: 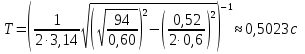  в) множитель  в выражении (7) представляет собой огибающую кривой колебаний:  г) смещение, скорость и ускорение тела в момент времени t1 = 2.5 с для затухающих колебаний получим по выражению (7), выполняя дифференцирование выражение (7) (для скорости и ускорения) и подставляя числовые значения параметров:               Смещение, скорость и ускорение тела в момент времени t = 2,5 с для затухающих колебаний соответственно равны: x(t) 0.0333; V(t) 0,0604; a(t) -5,2747. График смещений затухающих колебаний системы x(t) представлен на рисунке 3. 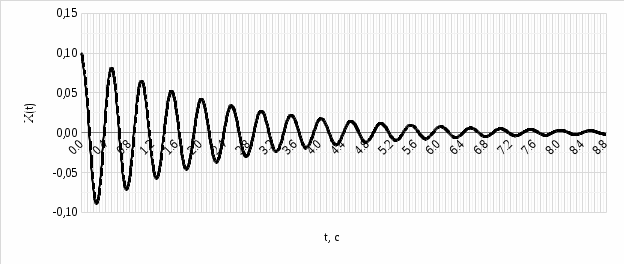 Рисунок 3. График смещений затухающих колебаний системы x(t) Ответ: а)  б)  в)  ;г) x(t) 0.0333 м; V(t) 0,0604 м/с; a(t) -5,2747 м/с2. Задание 2. Подводная лодка водоизмещением V движется горизонтально со скоростью υ на глубине H от поверхности моря. Средняя плотность лодки ρ1. В момент t0 = 0 лодка начинает всплытие. Сопротивлением воды пренебречь. Определить: а) время t1, когда лодка всплывет на поверхность моря; б) расстояние L, которое пройдет лодка в горизонтальном направлении в момент всплытия; в) вертикальную скорость u лодки; г) траекторию движения подводной лодки в координатах (l, h); д) тип соответствующей кривой. Плотность воды принять равной ρ0 = 10-3 кг/м3. . Сделать чертеж Решение: Дано: V = 1150 т = 1,15 106 кг U = 15 км/ч = 4,1667 м/с Н = 300 м ρ1 =0,5 10-3 кг/м3 p0 = 10-3 кг / м3 Модель должна позволять: – вычислять положение лодки в любой момент времени всплытия; – определять дальность расстояния от начала всплытия до конца всплытия; – скорость в момент всплытия, траекторию движения. По закону Архимеда на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости в объеме тела. Горизонтальная скорость υ - скорость подводной лодки в начале всплытия. Глубина начала всплытия Н. ρ0 - плотность воды; ρ1 - средняя плотность лодки. Примем следующие гипотезы: – объектом моделирования является подводная лодка, которую будем считать точкой массы m, сосредоточенной в центре масс. – движение происходит в поле сил тяжести. – при малых скоростях силами сопротивления можно пренебречь: скорость подводной лодки примерно 1/10 υ . – плотность воды не меняется в процессе всплытия в зависимости от температуры воды, тогда сила Архимеда будет величиной постоянной. – ρ1 - средняя плотность лодки, не содержащей балластной воды. – всплытие происходит в вертикальной плоскости, проходящей через вектор начальной скорости при отсутствии боковых течений и вертикальных течений. 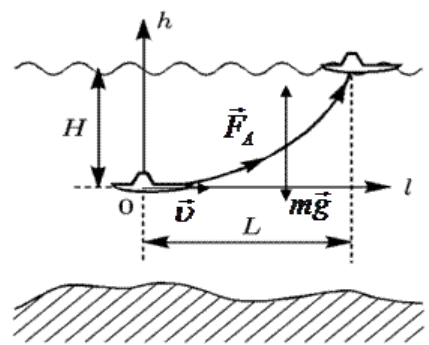 Рисунок 4. Рисунок к задаче 2 Используем второй закон Ньютона, если на тело массой m действует сила  , то оно движется в направлении действия силы с ускорением  , пропорциональным силе и обратно пропорциональным массе тела, т.е. где - главный вектор сил, действующих на тело. тогда получим математическую модель в векторной форме (8):
Для перехода к скалярной форме составим проекции уравнения (8) на оси выбранных координат. Начало движения возьмем в точке О. Обозначим через V1 объем подводной лодки в м3. Тогда: V1 = V / ρ0. Масса подводной лодки во время всплытия может быть определена произведением: m = V1 ρ1 На подводную лодку вертикально вверх действует выталкивающая сила Архимеда: FA = V1 ρ0 g, где g - ускорение свободного падения. Также в вертикальном направлении – но уже вниз – на лодку действует сила тяжести (вес лодки): P = mg = V1 ρ1 g Положительная разность сил и  обеспечивает подъём лодки в вертикальном направлении Н.Уравнение движения лодки может быть записано в виде (9):
где  - ускорение движения лодки в вертикальном направлении (отсчитывается от поверхности моря вглубь моря). То, что  показывает, что лодка должна всплывать.Перенесём отсчёт времени на момент начала всплытия и запишем задачу Коши для уравнения (9) в виде:
Разделив обе части на  , получим (11):
(вертикальная скорость в начальный момент равна нулю). Таким образом, мы построили математическую модель рассматриваемой системы в виде задачи Коши для ОДУ 2го порядка. 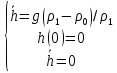 Решим задачу (11) с учетом (12):
1) Момент времени, когда лодка всплывет на поверхность моря, определим по значению  из выражения (14) при котором  Решая уравнение, получим:
Подставляя числовые значения параметров в (14), получим:  Таким образом, t = t0 + tk = t0 + 7,82 с. Координата l, характеризующая горизонтальное положение подлодки, изменяется по закону движения тела с постоянной скоростью:
т.е. по горизонтали l лодка перемещается равномерно со скоростью  . Следовательно, зависимость от времени можно представить линейной связью (16):
Подставляя в (16) время всплытия, получим расстояние, которое пройдет лодка в горизонтальном направлении от начала до окончания этапа всплытия:  L = 4,1667 7,82 = 32,60 м. 3) Для нахождения вертикальной скорости лодки достаточно продифференцировать по времени t выражение (13):
 Вертикальная скорость подводной лодки: u = 76,68 м/с. 4) На рисунке 5 показан график зависимости h(t) при изменении времени от 0 до 12 с: 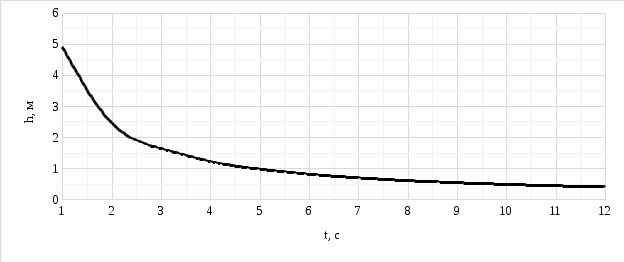 Рисунок 5. график зависимости h(t) при изменении времени от 0 до 12 с Из уравнения (16) выражаем время:
Подставляя (16) в уравнение (13), находим траекторию движения подводной лодки в координатах (l,h):
которая представляет собой параболу с вершиной в точке l = 0, h = 0. Траектория движения подводной лодки в координатах (l, h) показана на рисунке 6 в интервале изменения l от 0 до 60. 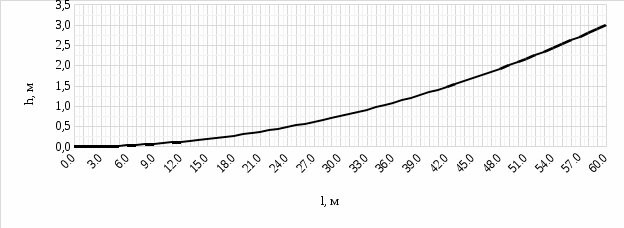 Рисунок 6. Траектория движения подводной лодки в координатах (l, h) 5) подставляя числовые значения параметров в (17), получим:
Итак, непосредственное применение закона Архимеда, определяющего величину выталкивающей силы, и закона Ньютона, связывающего силу, действующую на тело, и его ускорение, позволило легко найти траекторию движения подводной лодки. Ответ: 1)  2) L = 32,60 м; 3) u = 76,68 м/с; 4) рисунок 6; 5) тип кривой – парабола;  Задание 3. Канат длиной L и диаметром d лежит на плоской горизонтальной поверхности. Один конец его свободно свисает с поверхности вниз. Канат находится в состоянии равновесия. В некоторый момент времени канат начинает соскальзывать с поверхности под действием силы тяжести. Определить: 1) длину 0 < l < L части каната, покоящуюся на поверхности, когда канат еще находится в состоянии равновесия; 2) закон движения каната s(t); 3) скорость v(t) и ускорение a(t) каната в момент полного соскальзывания с поверхности. Плотность каната равна ρ = 0,3·103 кг/м3. Коэффициент трения составляет k = 0,2. Ускорение свободного падения принять равным g = 10 м/сек2. Сделать чертеж. Решение:
1) определим длину 0 < l < L части каната, покоящуюся на поверхности, когда канат еще находится в состоянии равновесия. I. Часть каната, лежащая на поверхности. l – длина части каната; m1 – масса части каната; На указанную часть каната действуют силы:  проекция на ось х: Fтр = F kN = F проекция на ось y: Fт1 = N m1g =N ρ π l d2 g = N Таким образом,
II. Часть каната, свисающая с поверхности вниз. L – l – длина части каната; m2 – масса части каната. На указанную часть каната действуют силы:  проекция на ось х отсутствует. проекция на ось y: Fт2 = F m2g = F
Подставив полученное выражение для F в уравнении (19) в уравнение (20), получим: k ρ π l d2 g = ρ π (L – l) d2 g после преобразований получим выражение (21):
подставим численные значения:  Длину части каната, лежащую на поверхности можно определить другим способом. Соскальзывание каната начнется в тот момент, когда сила тяжести свисающего конца превысит силу трения: 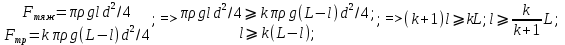   Равнодействующая сил тяжести и трения прикладывается ко всей массе каната. Ускорение, скорость и изменение длины свисающего конца равны:      Решая полученное интегральное уравнение, получаем:    Определим время полного соскальзывания каната t1. В этот момент  .    Ответ: 1) l = 8.33 м; 2) 3)  ;  Задача 4. На медной проволоке длиной l = 1 м и диаметром d подвешена пустая емкость. В дне целиком заполненного водой цилиндрического бака высотой H = 1 м и диаметром D = 5 дм сделано отверстие круглой формы диаметром d1 , из которого вода перетекает в пустую емкость. Найти: а) объем V вытекающей из бака воды за время t; б) время t1, когда бак полностью опустеет; в) зависимость длины проволоки от времени; г) объем воды в емкости, длину проволоки и момент времени t2, в который произойдет разрыв проволоки. Предел прочности проволоки равен σ = 2,2·108 Па. Плотность воды составляет ρ = 1,0·103 кг/м3 . Массой проволоки и емкости пренебречь. Построить графики функций V = V(t) и l = l(t). Задание 4 решить аналитически, а также с помощью математического пакета Maxima d = 2 мм, d1 = 1,5 см; Решение: Выведем зависимость объема вытекающей воды от времени: 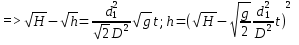 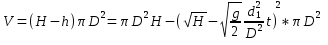     б) 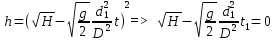 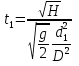 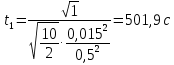 в) По закону Гука, удлинение Δl равно:  где Е = 1011 Па – модуль нормальной упругости для Си.  г) Объем вытекшей воды, при котором произойдет обрыв проволоки:      Удлинение проволоки на момент обрыва Δl равно:  Графики функций V = V(t) и l = l(t) представлены на рисунках 8 и 9. 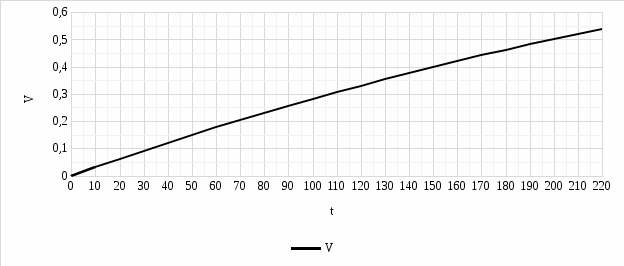 Рисунок 8. Зависимость объема вытекшей воды V от времени t 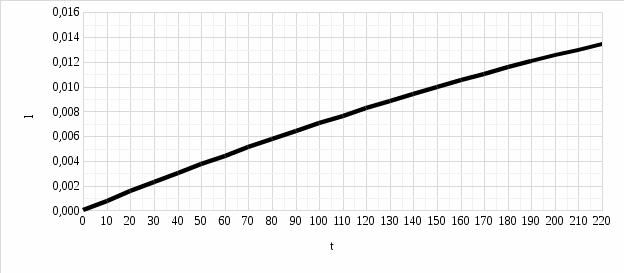 Рисунок 9. График зависимости величины удлинения проволоки l от времени t Ответ: а) ;б) t1 = 501,9 с; в) г) V =0.691150 м3; t2 = 22,59 с; l = 0,001728 м. Задача 5. Пусть заданы координаты точек А и С плоскости. Точка В лежит на прямой y = 0. Используя вариационные принципы построения математических моделей, найти: а) условие, при котором ломаная АВС имеет наименьшую длину; б) числовое значение этого условия; в) наименьшую длину ломаной АВС. Сделать чертеж. Задание 5 решить аналитически, а также с помощью математического пакета Maxima А(-5;10), С(25;15); Решение: а) Для луча света, расстояние, пройденное лучом от точки до точки, будет наибыстрейшим. Для однородной среды (v = const) оно будет и кратчайшим. Для луча угол падения равен углу отражения, следовательно, угловые коэффициенты линий АВ и ВС будут отличаться только знаками. б) Найдем уравнения линий, при которых lAB + lBC = min. 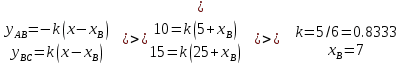 в) Определим АВСmin: 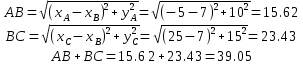 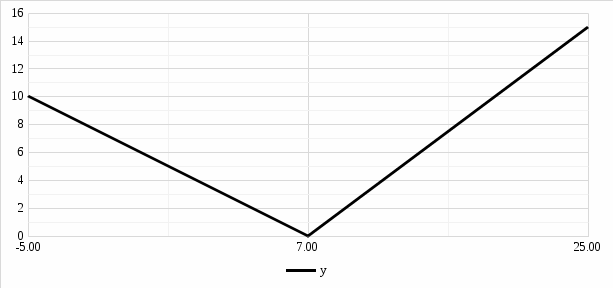 Рисунок 10. Точки A, B, C на плоскости Ответ: а) расстояние, пройденное лучом от точки до точки, будет наибыстрейшим; б) k = 0.83; xB = 7 в) АВС = 39,05 |
