Механическая система
 Условие
Факультет 1
Индекс группы Б
Цифра группы 8
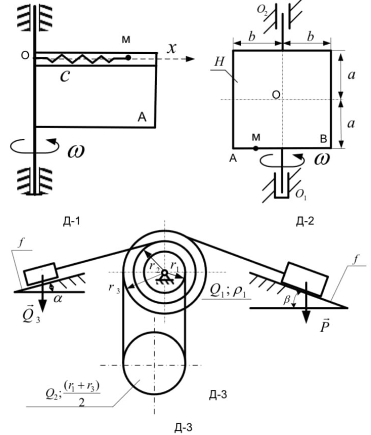
Механическая система, изображённая на рис. Д-3, состоит из трёх тел, соединённых не растяжимыми и не провисающими нитями; при этом тела системы совершают поступательное движение (груз Р), вращаются вокруг неподвижной горизонтальной оси (соосные блоки 1, жёстко насаженные на единую ось), совершают плоскопараллельное движение (однородный диск 2). При выполнении задания необходимо: 1. Составить математическую модель для определения движений всех тел механической системы, а так же реакций внешних и внутренних связей в виде замкнутой системы дифференциальных и алгебраических уравнений. 2. Для груза Р получить дифференциальное уравнение движения. 3. Для груза Р получить дифференциальное уравнение движения используя теорему об изменении кинетической энергии. 4. Решить полученное в пунктах 2 и 4 дифференциальное уравнение при заданных начальных условиях. 5. Получить математическую модель для анализа условий равновесия рассматриваемой механической системы. Q1 = 20 Н;Q2 = 10 Н r1 = 0,10 м;r2 = 0,12 м ρ1 = 0,15 м;f = 0,1 k = 0,005;q0 = 0,4 м q0 = 0,2 м/с;P = 5 Н M = 3 Н ∙ м;α = 30◦
Ответ
Движение груза массой Р описывается уравнением S = f(t) = 2,39t2 + 0,2t + 0,4, которое было получено двумя разными методами. Для того, чтобы исследуемая система находилась в равновесии вес груза должен быть в пределах 16,11 ≤ P ≤ 25,83 Н.
Решение
1. Груз P движется поступательно, соосный блок 1 вращается, цилиндр 2 совершает плоское движение – качение. Точка касания цилиндра с поверхностью качения является МЦС тела 2.
Принимаем в качестве обобщённой координаты перемещения груза P ивыражаем все угловые и линейные скорости через V
ω1 = Vr1V1 = ω1r2 = r2r1 V
V12 ∙0,5r2 = V20,5r2 = ω2ω2 = V1r2 = r2r1r2 V = Vr1
V2 = ω2 ∙ 0,5r2 = 0,5r2r1 V = r22r1 V
Составляем таблицу кинематических связей
T= T1+T2+T3.(1.2)
Груз 1 совершает поступательное движение. Его кинетическая энергия равна:
T1= 1/2 m1*υ21(1.3)
где Vl - скорость груза 1.
Блок 2 совершает вращательное движение около неподвижной оси. Его кинетическая энергия
T2=1/2*m2* υ22+1/2*Jc2 ω 22(1.4)
где
Jn2 = m2*i22: - момент инерции относительно центральной оси блока;
ω2- угловая скорость блока.
Блок 3 совершает вращательное движение,
T3=1/2*Jc3 ω 23 где jc3=1/2 m3*r23 (1.5)
Каток 4 совершает плоскопараллельное движение
T =1/2*m4 *vc42 +1/2*Jc4 * ω 42 где Jc4 = ½*m4 *r4 2
Кинетическая энергия всего механизма будет равна:
T=1/2m1υ12+ 1/2m2 *vc22 +1/2*Jc2 ω 22 + 1/2*Jc3 ω 23 + 1/2*m4 *vc42 + 1/2*Jc4 *ω 42 (1.6)
Выразим υn3.,ω2,ω3 через скорость груза 1
vc2 = υ1=υ=S; => ω 3= (R2 + r2)*v/R 3*V3 vc4 =ω 4* r 4 = (R2 + r2)*v/2R2 (1.7)
ω 2 =v/r 2
Подставляя (1.3), (1.4), (1.5), в (1.6) с учетом (1.7), и вынося 1/2 и V2 за скобки, получаем:T= 1/2(m +m + Jc2 т пр /R2 2 + Jc3 * (R2 - r 2 ) 2 / R2 * r 2 + m4 (R2 + r 2 ) 2 /4r22 + Jc4(R2 - r 2 ) 2 /4r22 R2 2 )* υ2
T=1/2m трv3 2(1-8)
т пр =m +m2 +m3 1/ R2 2 + 1/2m3 (R2 - r 2 ) 2 / R2 + m4 (R2 + r 2 ) 2 /4r22 + m4 (R2 + r 2 ) 2 /4r22
т пр=8, 21кг(1-9)
Найдем производную от кинетической энергии по времени:
dT/dt= т пр – S*S(1.10)
вычислим сумму мощностей внешних и внутренних сил.
Мощность силы равна скалярному произведению вектора силы на скорость точки ее приложения:
N = FV = Fvcos(F, v);(1-11)
Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, недеформируемые и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:
∑N’=0(1.12)
Будут равняться нулю и мощности некоторых внешних сил, в том числе сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы N4, ,Y3,X3,P3,Fвд. Сумма мощностей внешних сил:
N=F*V+pV-RV+p2V2-Fупр*V4
С учетом кинематических соотношений (1.7) сумму мощностей внешних сил преобразуем к виду:
(1-13) N= F(t)*V1 +p1 V1 -RV1 + p2V1 -Fупр V1 * R2 +r2 /2R2 ,
N =( F(t) +p1 – R +p2 - Fупр R2 +r2 /2R2)V1 , или
N= Fпр * V
Где Fnp приведенная сила.
Упругую силу считаем пропорциональной удлинению пружины. которое равно сумме статического ƒст и динамического S4 удлинений
Fупр=с(ƒст + S4 ) (1-15)
Сила вязкого сопротивления R =μ V = μ S тогда
Fпр = F(t)+p1 – μ*S+ p 2 – c(ƒст + R2 +r2 /2R2 * S) R2 +r2 /2R2 , (1-16)
В состоянии покоя приведенная сила равна нулю.
Пологая в (1-16) , что S=’S=0 и F(t)= 0 получаем условие равновесия
Fпр = p + p2 = c *ƒст= R2 +r2 /2R2 =0, (1-17)
Отсюда статистическое удлинение пружины равно:
- c *ƒст R2 +r2 /2R2 = -p1- p ;
ƒст R2 +r2 /2R2 =(p 1 + p 2 )/c => ƒст =(p 1 + p 2 )/c* 2R2 / R2 +r2
ƒст =1/c (p 1 + p2) * 2R 2/R2 +r2 ; (1-18)
Подставляем выражение (1-18) в, (1-16) получаем окончательное выражение для приведенной силы .
ƒпр = F(t) + p1 +p2 - μS – c* R2 +r2 /2R 2 *1/c (p 1 + p2)* *2R 2/R2 +r2- c*(R2 + r2 ) 2/4R22 *S
ƒпр = F(t) - μS- c*(R2 + r2 ) 2/4R22 *S; (1-19)
Подставим выражение для производной от кинетической энергии и сумму мощностей всех сил с учетом (1-19) в (1-1) полуучаем дифференциальное уравнение движения системы ;
mпр =S=- c*(R2 + r2 ) 2/4R22 *S- μS+ F0 sin(pt) (1-20)
S = 2nS +k2 S +F0 / mпр sin(pt) ; (1-21)
Где k циклическая частота свободных колебаний ;
n = μ/2* mпр =100/2*8.21= 6.1с -1 ;
n – показатель степени затухания колебаний ;
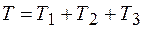 . .
Кинетическая энергия груза 1, движущегося поступательно, равна:
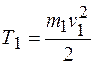 . .
Кинетическая энергия блока 2, совершающего вращение вокруг оси Оz, перпендикулярной плоскости чертежа:
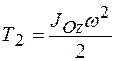 . .
Кинетическая энергия тела 3 в его поступательном движении:
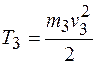 . .
Таким образом,
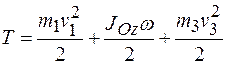 . .
Выражение кинетической энергии содержит неизвестные скорости всех тел системы. Начать определение необходимо с 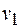 . Избавимся от лишних неизвестных, составив уравнения связей. . Избавимся от лишних неизвестных, составив уравнения связей.
Уравнения связей это не что иное, как кинематические соотношения между скоростями и перемещениями точек системы. При составлении уравнений связей выразим все неизвестные скорости и перемещения тел системы через скорость и перемещение груза 1.
Скорость любой точки обода малого радиуса 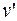 равна скорости тела 1, а также произведению угловой скорости тела 2 и радиуса вращения r: равна скорости тела 1, а также произведению угловой скорости тела 2 и радиуса вращения r:
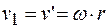 . .
Отсюда выразим угловую скорость тела 2:
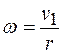 . (а) . (а)
Вращательная скорость любой точки обода блока большого радиуса 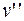 , с одной стороны, равна произведению угловой скорости блока и радиуса вращения, а с другой – скорости тела 3: , с одной стороны, равна произведению угловой скорости блока и радиуса вращения, а с другой – скорости тела 3:
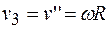 . .
Подставив значение угловой скорости, получим:
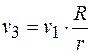 . .
Проинтегрировав при начальных условиях выражения (а) и (б), запишем соотношение перемещений точек системы:
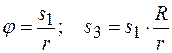 . .
Зная основные зависимости скоростей точек системы, вернемся к выражению кинетической энергии и подставим в него уравнения (а) и (б):
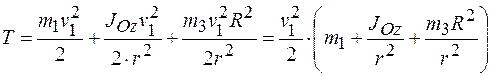 . .
Момент инерции тела 2 равен:
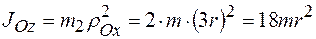 . .
Подставляя значения масс тел и момента инерции тела 2, запишем:
 . .
Определение суммы работ всех внешних сил системы на заданном перемещении.
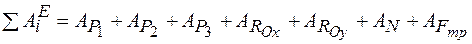 . .
Работа силы тяжести тела 1
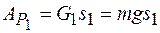 . .
Работа сил 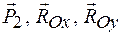 равна нулю, так как эти силы приложены к неподвижной точке. равна нулю, так как эти силы приложены к неподвижной точке.
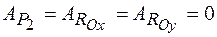 . .
Работа силы тяжести тела 3
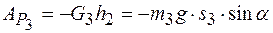 . .
Работа нормальной реакции тела 3 равна нулю, так как сила перпендикулярна направлению движения
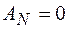 . .
Работа силы трения скольжения
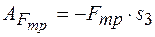 , ,
так как
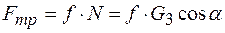 , ,
тогда
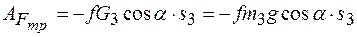 . .
Сумма работ внешних сил
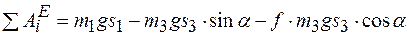 . .
Подставляя значения масс тел, соотношения перемещений (в) и числовые параметры, запишем:
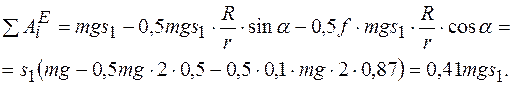
Теперь согласно теореме об изменении кинетической энергии механической системы приравняем значения Т и 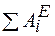
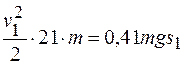 . (г) . (г)
Скорость тела 1 получим из выражения (г)
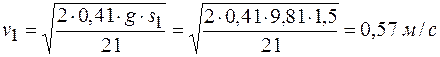 . .
Ускорение тела 1 можно определить, продифференцировав по времени равенство (г):
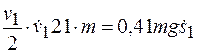 , ,
где 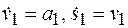 . .
Тогда
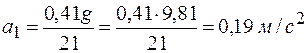 . . |
 Скачать 113.37 Kb.
Скачать 113.37 Kb.