вариант 4. Решение Шаг 1
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
Задача 2При подкормке посевов необходимо внести на 1 га почвы не менее 8 единиц химического вещества А, не менее 21 единиц химического вещества В и не менее 16 единиц химического вещества С. Агрофирма закупает комбинированные удобрения двух видов I и П. В таблице указано содержание количества единиц химического вещества в 1 кг каждого вида удобрений и цена 1 кг удобрений. Определите потребность агрофирмы в удобрениях I и II вида на 1 га посевной площади при минимальных затратах на их приобретение.
Задание 1. Сформулировать экономико-математическую модель исходной экономической задачи. Задание 2. Решить полученную задачу линейного программирования графическим методом. Задание 3. Сформулировать двойственную задачу и найти ее оптимальное решение, используя теоремы двойственности. Решите графическим методом задачу линейного программирования. Найдите минимум целевой функции f(X) при заданных ограничениях: 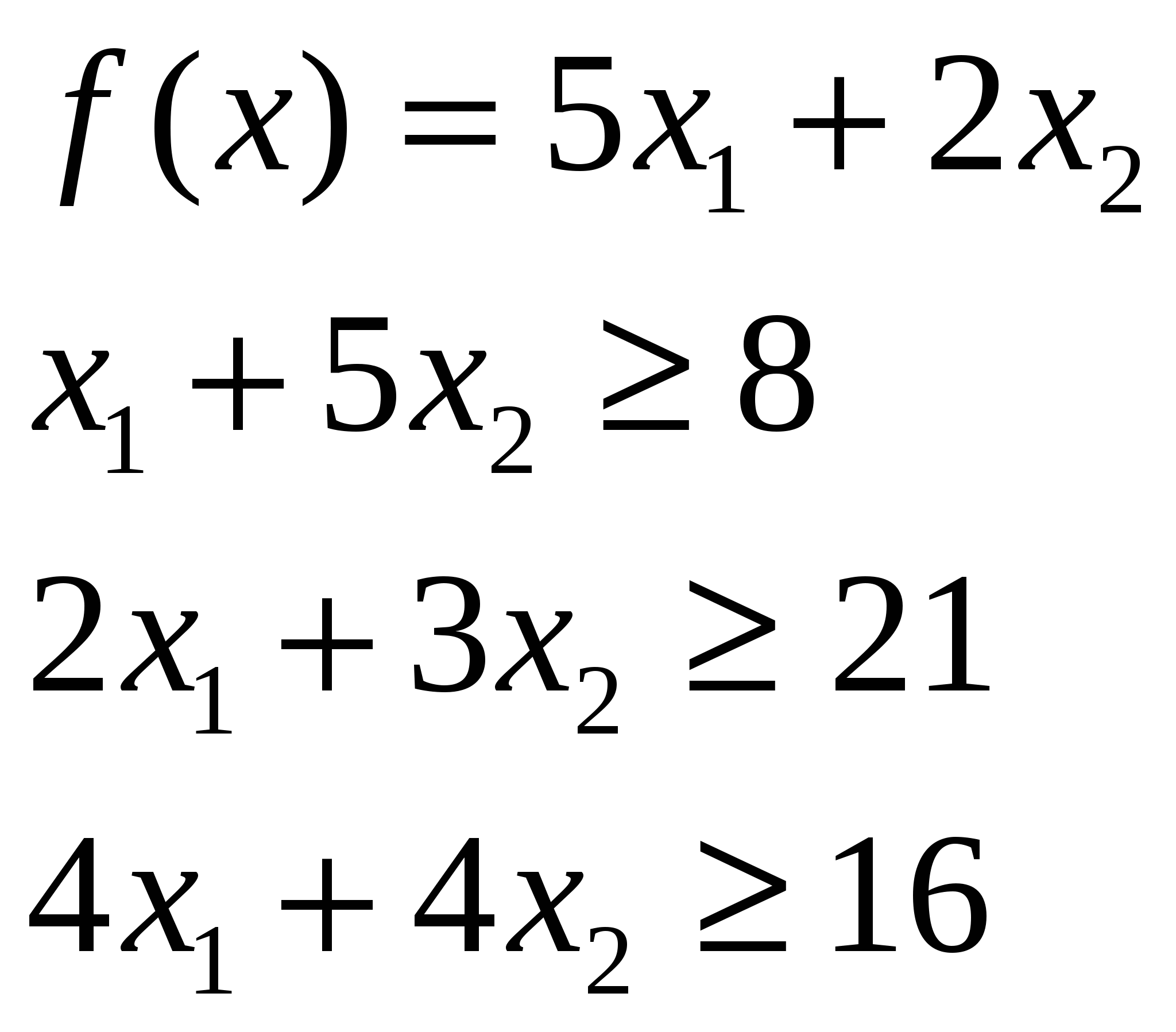 Решение Для построения прямых всех ограничений построим таблицу 1. Таблица 1
Целевая функция задачи с двумя переменными геометрически представляет собой плоскость в пространстве, пересекающую координатную плоскость {x1;0;x2}. Линией пересечения этих плоскостей является показанная на рис. 1 линия нулевого уровня целевой функции [f(x)=0] – прямая, в каждой точке которой целевая функция равна нулю. Линия нулевого уровня проходит через начало координат и расположена перпендикулярна вектору-градиенту целевой функции - направлению в координатной плоскости {x1;0;x2}, соответствующему наискорейшему возрастанию целевой функции. В нашей задаче с1=5, с2=2. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
