вариант 4. Решение Шаг 1

• Название: Решение Шаг 1
• Дата: 26.04.2018
• Размер: 0.65 Mb.
• Имя файла: вариант 4.doc
• Тип: Решение; #42260
• страница: 7 из 8

Задача 4

В таблице приведены годовые данные о трудоёмкости производства 1т цемента (нормо-смен):

Текущий номер года(t)	1	2	3	4	5	6	7	8	9	10
Трудоёмкость 1т цемента (yt)	7,9+0,4	8,3+0,4	7,5+0,4	6,9+0,4	7,2+0,4	6,5+0,4	5,8+0,4	4,9+0,4	5,1+0,4	4,4+0,4

Решение

1. 
   Построить вспомогательную таблицу для исследования линейной модели.
   

t	Yi	t-tcp	Yi-Ycp	(t-tcp)^2	(t-tcp)*(Yi-Ycp)	Yрасч	Ет
1	8,3	-5	1,45	25	-7,25	8,7	-0,4
2	8,7	-4	1,85	16	-7,4	8,3	0,37
3	7,9	-3	1,05	9	-3,15	8,0	-0,06
4	7,3	-2	0,45	4	-0,9	7,6	-0,29
5	7,6	-1	0,75	1	-0,75	7,2	0,38
6	6,9	1	0,05	1	0,05	6,5	0,42
7	6,2	2	-0,65	4	-1,3	6,1	0,09
8	5,3	3	-1,55	9	-4,65	5,7	-0,44
9	5,5	4	-1,35	16	-5,4	5,4	0,13
10	4,8	5	-2,05	25	-10,25	5	-0,2
Ycр	6,85			110	-41
-0,37	а1
6,85	а0

Пов.точка	Ет^2	Et-Et-1	(Et-Et-1)^2	EtEt-1
	0,16
1	0,1369	0,77	0,5929	-0,148
1	0,0036	-0,43	0,1849	-0,0222
0	0,0841	-0,23	0,0529	0,0174
1	0,1444	0,67	0,4489	-0,1102
0	0,1764	0,04	0,0016	0,1596
0	0,0081	-0,33	0,1089	0,0378
1	0,1936	-0,53	0,2809	-0,0396
1	0,0169	0,57	0,3249	-0,0572
1	0,04	-0,33	0,1089	-0,026
	0,964	0,2	2,1048	-0,1884

Проверку адекватности построенной модели проведем на основе исследования случайности остаточной компоненты по критерию пиков.

	t	Yi	Yp	e	Точки пиков
	1	8,3	8,7	-0,4	-
	2	8,7	8,3	0,37	1
	3	7,9	8,0	-0,06	1
	4	7,3	7,6	-0,29	0
	5	7,6	7,2	0,38	1
	6	6,9	6,5	0,42	0
	7	6,2	6,1	0,09	0
	8	5,3	5,7	-0,44	1
	9	5,5	5,4	0,13	1
	10	4,8	5	-0,2	1
сумма	55	68,5	68,5	0	6

Используя формулы:




В нашем случае р =8 а неравенство выглядит следующим образом: 6>2 , т.е. неравенство выполняется. Следовательно, можно сделать вывод, что свойство случайности ряда остатков подтверждается.

2. Для оценки адекватности построенных моделей на основе исследования независимости уровней ряда остатков по d- критерию строим дополнительные столбы в нашей таблице:

t	Yi	Yp	e	Точки пиков	Ет^2	Et-Et-1	(Et-Et-1)^2	Ei/Yi*100
1	8,3	8,7	-0,4	-	0,16			4,82
2	8,7	8,3	0,37	1	0,1369	0,77	0,5929	4,25
3	7,9	8,0	-0,06	1	0,0036	-0,43	0,1849	0,76
4	7,3	7,6	-0,29	0	0,0841	-0,23	0,0529	3,97
5	7,6	7,2	0,38	1	0,1444	0,67	0,4489	5,00
6	6,9	6,5	0,42	0	0,1764	0,04	0,0016	6,09
7	6,2	6,1	0,09	0	0,0081	-0,33	0,1089	1,45
8	5,3	5,7	-0,44	1	0,1936	-0,53	0,2809	8,30
9	5,5	5,4	0,13	1	0,0169	0,57	0,3249	2,36
10	4,8	5	-0,2	1	0,04	-0,33	0,1089	4,17
55	68,5	68,5	0	6	0,964	0,2	2,1048	41,18

Используя формулу 5.12, получаем d = 2,1048/0,964=2,1834

Эта величина превышает 2, что свидетельствует об отрицательности автокорреляции, поэтому критерий Дарбина –Уотсона необходимо преобразовать:d’ =4 – d = 4 – 2,18 = 1,82. Данное значение сравниваем с двумя критическими табличными значениями критерия, которые для линейной модели в нашем случае можно принять равными d₁=1,08 и d₂=1,36. Так как расчетное значение попадает в интервал от d₂ до 2, то делается вывод о независимости уровней остаточной последовательности. Отсюда следует, что остаточная последовательность удовлетворяет всем свойствам случайной компоненты временного ряда, значит, построенная модель является адекватной. Для характеристики точности модели воспользуемся показателем средней относительной ошибки аппроксимации, который рассчитывается по формуле 5.14: Еотн.ср. = 41,18/10=4,1175 (%). Полученное значение средней относительной ошибки говорит о достаточно высоком уровне точности построенной модели.
Оценка нормального распределения.

- нормированный размах R = Ε_max – Ε_min=0,42-(-0,44)=0,86;

S = σ_ε=0,3;

= = 2,3; так как этот показатель не входит в диапазон 2,7÷3,7 ,то => остатки не распределены нормально;

Т.к. не все 4 гипотезы выполнились, то модель нельзя считать полностью адекватной исследуемого процесса.

V. Оценка точности.

Найдем среднюю относительную ошибку расчета.

Δ_ср=== 4,118%; => точность приемлемая
VI. Прогнозирование.

1. Точечный прогноз, используя экстраполяцию.

=6,85-0,37t

Найдем прогноз на две недели вперед:

д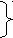ля t =10 = 6,85 -0,37×10 = 3,15;

для t =11 = 6,85 -0,37×11 = 2,78; это ожидаемые значения спроса;
2. Найдем возможные отклонения от спрогнозированных значений, т.е. ширину доверительного интервала:

u_k = 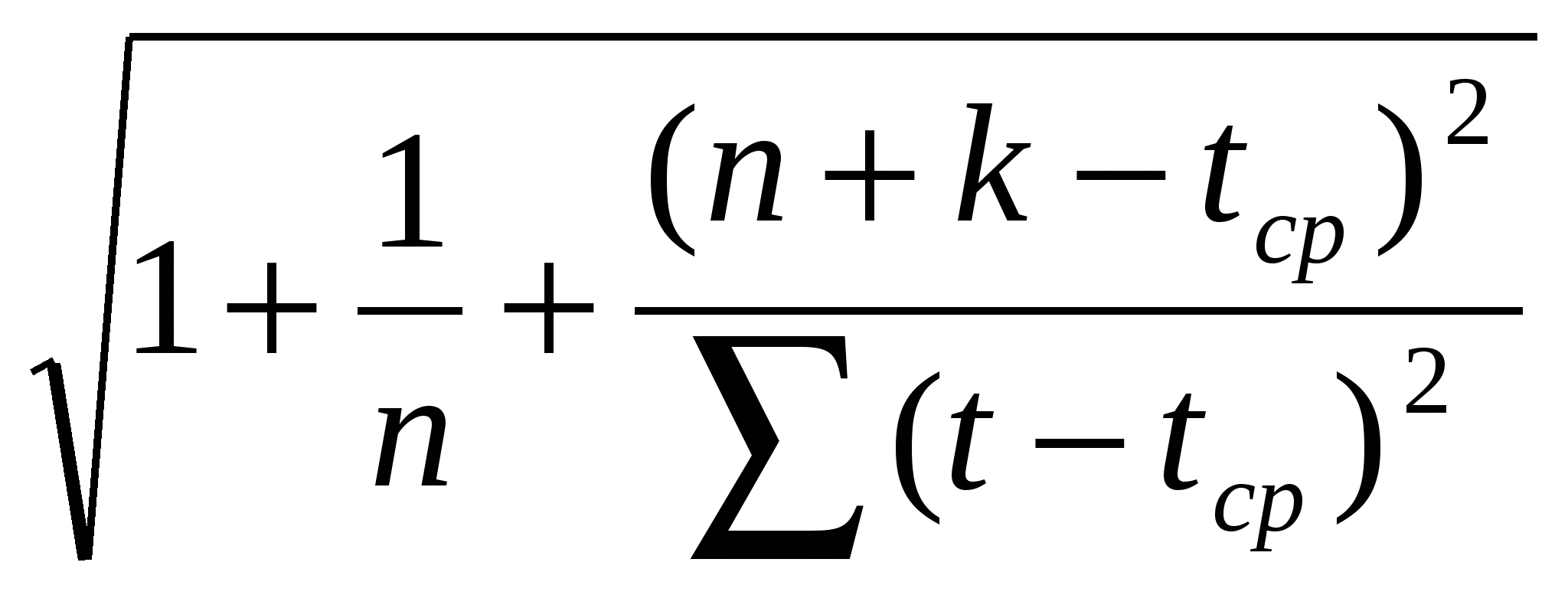× S_ε×;

если Р = 70 %, то =1,13;

S_ε = = 0,5;

для t =10 k =1 u₁ = 0,37

для t =11 k =2 u₁ = 0,37

показатель	прогноз	Нижняя граница	Верхняя граница
	3,15 2,78	2,78 2,41	3,52 3,15	Р = 70%