вариант 4. Решение Шаг 1

• Название: Решение Шаг 1
• Дата: 26.04.2018
• Размер: 0.65 Mb.
• Имя файла: вариант 4.doc
• Тип: Решение; #42260
• страница: 8 из 8

Задача 5

В таблице представлены первый (х_ij) и второй (Y_i) квадранты схемы межотраслевого баланса производства и распределения продукции для трехотраслевой экономической системы (N- последняя цифра зачетной книжки студента, т.е. 3)

Производящие отрасли	Потребляющие отрасли			Конечная продукция
	1	2	3
1	200+10N	50+10N	300+10N	200+10N
2	150+10N	250+10N	0+10M	100+10N
3	230+10N	50+10N	150+10N	300+10N

Отрасли	Коэффициенты прямых затрат, aij			Конечный продукт, Y
	1	2	3
1	240	90	340	240
2	190	290	40	140
3	270	90	190	340

Решение

Расчет проводим с помощью табличного процессора MS Excel.

1. 
   Матрица полных затрат вычисляется по формуле:
   

В=(Е-А)^-1

	1	0	0
E=	0	1	0
	0	0	1

	-239	-90	-340
E-A=	-190	-289	-40
	-270	-90	-189

	0,005	0,001	-0,009
B=	-0,002	-0,004	0,005
	-0,006	0,000	0,005

2. Вектор валового выпуска определяется по формуле:

Х=(Е-А)^-1*Y=BY

	-1,67
X=	0,57
	0,32

3. Межотраслевые поставки продукции рассчитываются по формуле:

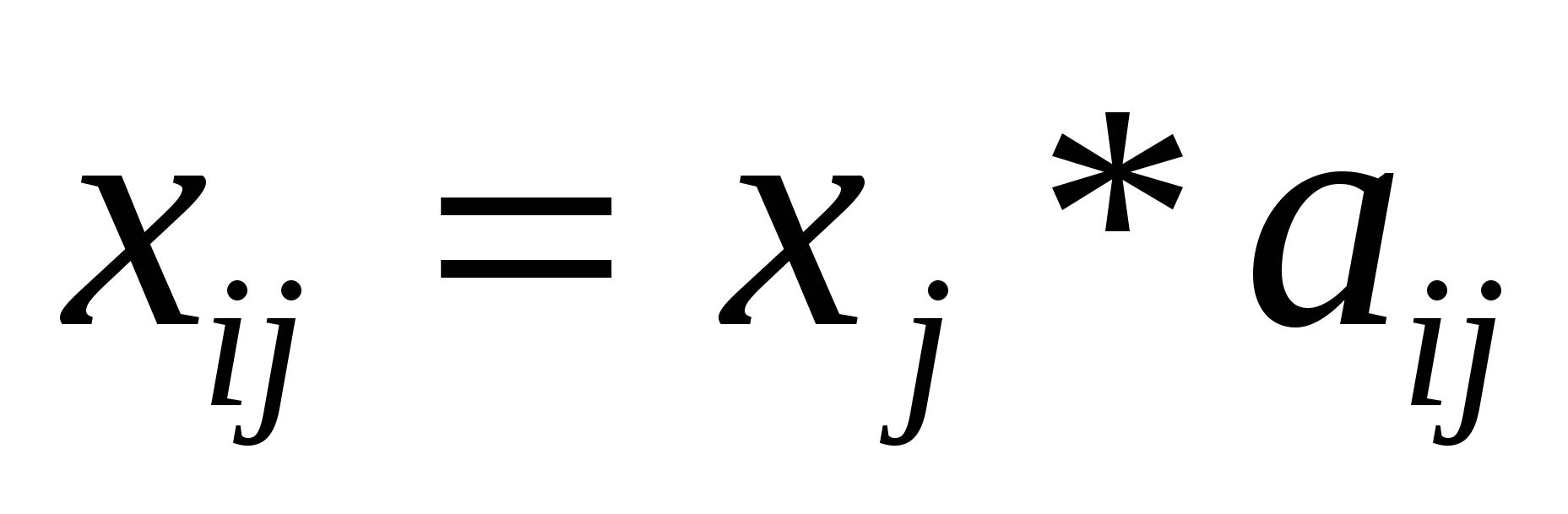
	-401,48	51,41	108,40
xij=	-317,84	165,66	12,75
	-451,67	51,41	60,58

4. Достаточным признаком продуктивности матрицы А является ограничение на величину ее нормы (норма матрицы – величина наибольшей из сумм элементов каждого столбца этой матрицы).

5. На основании рассчитанных выше значений построим схему межотраслевого баланса.

Производящие отрасли	Потребляющие отрасли			Конечная продукция Yi	Валовая продукцияXi
	1	2	3
1	-401,48	51,41	108,40	240,00	-1,67
2	-317,84	165,66	12,75	140,00	0,57
3	-451,67	51,41	60,58	340,00	0,32
Условно чистая продукция Zj	1169,32	-267,91	-181,41	720,00
Валовая продукция Xj	-1,67	0,57	0,32		-0,78