Способ сложения
|
умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
|
первое уравнение умножим на(-2), чтобы коэффициент при переменной х стал противоположным тому, что во втором уравнении
[
|
-10х-22у=-16
10х-7у = 74
|
|
2.складывают почленно левые и правые части уравнений системы;
|
|
3.решают получившееся уравнение с одной переменной
|
у=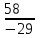 = -2 = -2
|
4.найденное значение переменой подставляют в одно из уравнений и находят значение второй переменной
|
5х+11∙(-2)=8 5х-22=8 5х=8+22 5х=30
х=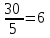
|
5.ответ.
|
Ответ:(6; -2) или х=6, у=-2
|
II Способ подстановки
|
выражают из какого-нибудь уравнения системы одну переменную через другую;(выбранную переменную оставляют в левой части, все остальное переносят в правую часть. Потом каждый компонент делят на число, стоящее при переменной, которая в левой части);
|
8у-х=4
-х=4-8у /:(-1)
х= -4+8у
|
2.подставляют в другое уравнение системы в место выбранной переменной полученное выражение;
|
2(-4+8у) -21у=2
|
3.решают получившееся уравнение с одной переменной;
|
-8+16у -21у=2
16у -21у =2+8 -5у=10 у=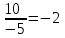
|
4.найденное значение переменой подставляют туда, где была выражена первая переменная и решают получившееся уравнение
|
Х= -4+8∙( -2) х=-4 -16 х= -20
|
5.ответ.
|
Ответ(-20; -2) или х=-20, у=-2
|
III Графический способ.
Строят графики каждого уравнения отдельно. Находят координаты точки пересечения графиков.
|
 Скачать 20.28 Kb.
Скачать 20.28 Kb.