Идз 8. – Вариант 13. Решение Случайная величина x может принимать значения x 0 0, x 1 1, x 2 2, x 3 3, x 4 4

• Название: Решение Случайная величина x может принимать значения x 0 0, x 1 1, x 2 2, x 3 3, x 4 4
• Дата: 27.11.2022
• Размер: 164 Kb.
• Имя файла: Идз 8. – Вариант 13.doc
• Тип: Решение; #814159

ИДЗ 18.2 – Вариант 13.
1. Найти закон распределения указанной дискретной CB X и ее функцию распределения F(x). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ(X). Построить график функции распределения F(x)
1.13. Вероятность приема каждого из четырех радиосигналов равна 0,6; СВ X – число принятых радиосигналов.
Решение:

Случайная величина X может принимать значения

x₀ = 0, x₁ = 1, x₂ = 2, x₃ = 3, x₄ = 4

Воспользуемся формулой Бернулли. Если производится n независимых испытаний, при каждом из которых вероятность осуществления события A постоянна и равна p, а вероятность противоположного события равна q = 1 – p, то вероятность того, что при этом событие A осуществляется ровно m раз, вычисляется по формуле



где – число сочетаний из n элементов по m.

Для данного случая n = 4; m = 0,1,2,3,4;

Вероятность принятых сигналов p = 0,6;

Не принятые сигналы q = 1– p = 1–0,6 = 0,4

Тогда запишем вероятности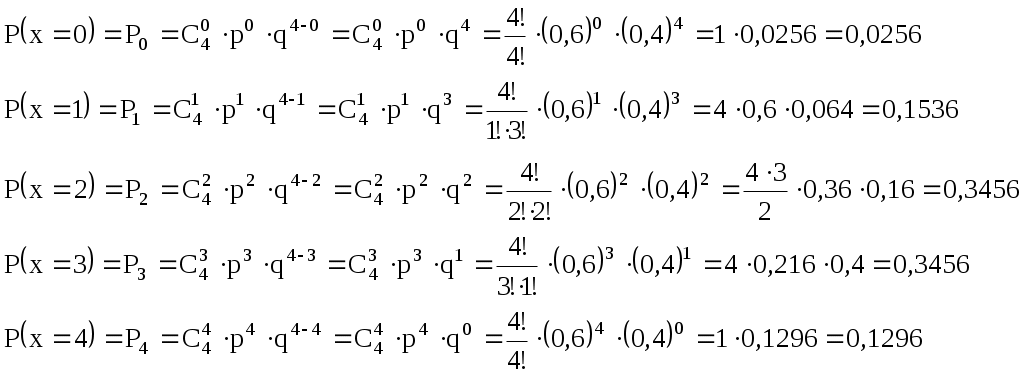



Таким образом, искомый закон распределения

Xi	0	1	2	3	4
p(i)	0,0256	0,1536	0,3456	0,3456	0,1296

Проверка: 0,0256+0,1536+0,3456+0,3456+0,1296=1

Составим функцию распределения: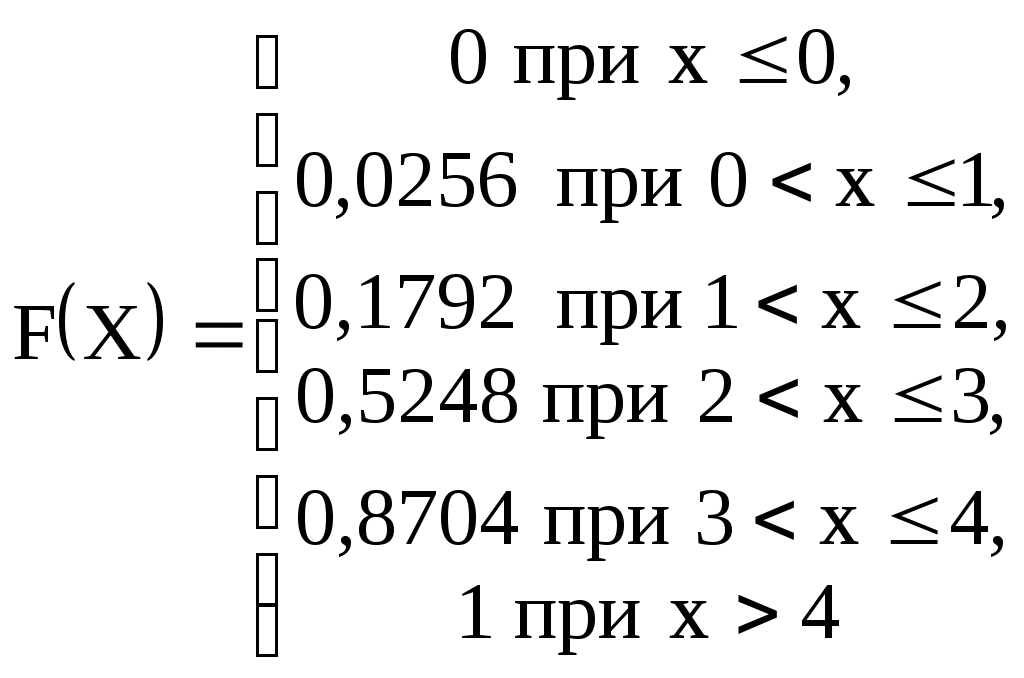


Выполним чертеж: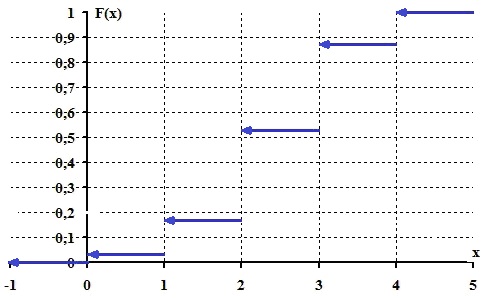


Вычислим математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение σ(X).

Математическое ожидание равно:





Дисперсия равна





Среднее квадратическое отклонение:



2. Дана функция распределения F(х) СВ X. Найти плотность распределения вероятностей f(x), математическое ожидание М(X), дисперсию D(X) и вероятность попадания СВ X на отрезок [а; b]. Построить графики функций F(х) и f(x).
2.13. 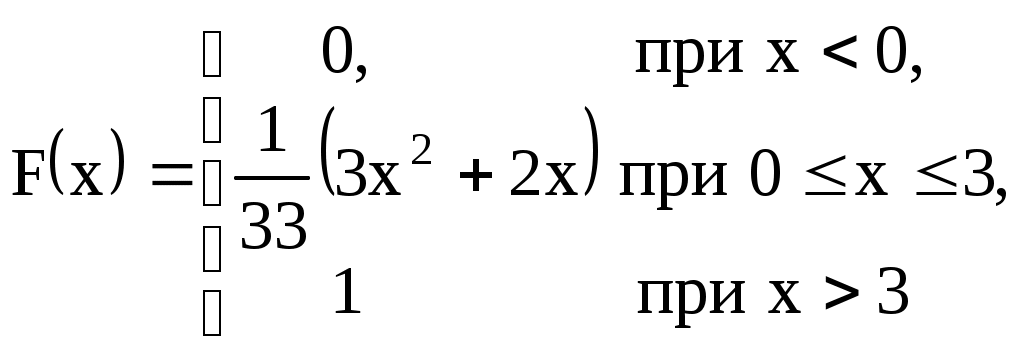a = 0, b = 2
Решение:

Найдем функцию плотности распределения вероятностей: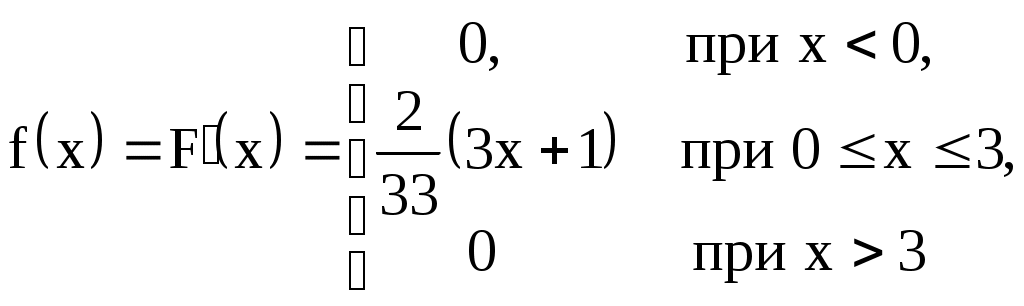



Построим графики функций F(х) и f(x)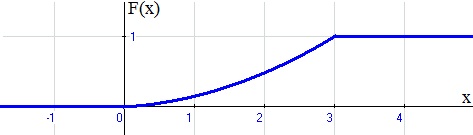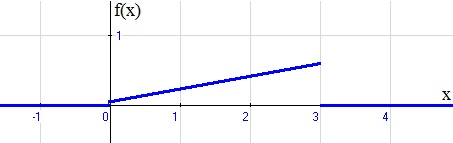



Вычисляем математическое ожидание и дисперсию.

Математическое ожидание определяется выражением



Тогда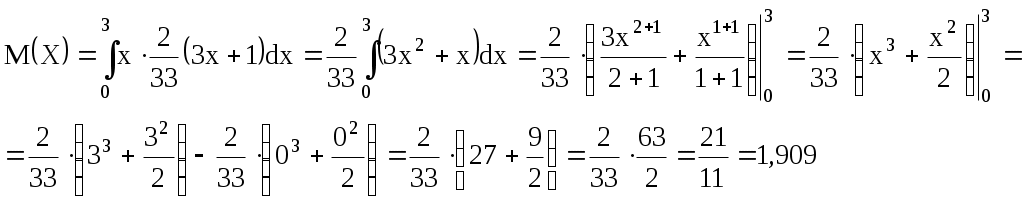



Вычисляем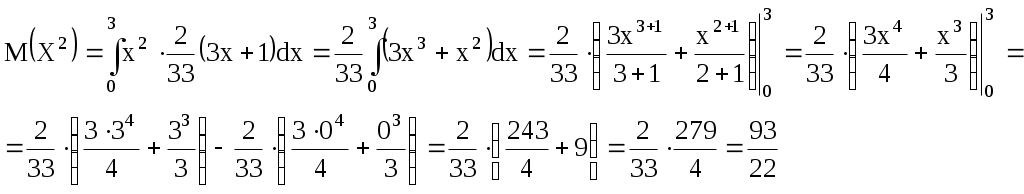



Дисперсия равна




Найдем вероятность того, что X примет значение из отрезка [0; 2]

- искомая вероятность

3. Решить следующие задачи.
3.13. Случайная величина подчинена закону Пуассона с математическим ожиданием а = 3 . Найти вероятность того, что данная СВ примет положительное значение.
Решение:

Для случайной величины Х, распределенной по закону Пуассона, найдем вероятность того, что она примет значение не меньшее заданного k. Эту вероятность обозначим R_k:



Очевидно, вероятность R_k может быть вычислена как сумма



Однако значительно проще определить ее из вероятности противоположного события:



В частности, вероятность того, что величина Х примет положительное значение, выражается формулой



Тогда вычисляем:



Ответ:


4. Решить следующие задачи.
4.13. Вероятность наличия зазубрин на металлических брусках, изготовленных для обточки, равна 0,2. Оценить вероятность того, что в партии из 1000 брусков отклонение числа пригодных брусков от 800 не превышает 5 %.
Решение:

Пусть вероятность наступления события в отдельном испытании равна p и при проведении n независимых испытаний ожидается наступление m событий. Предполагается, что частота наступления m/n близка к p.
Согласно теореме Бернулли, вероятность отклонения частоты m/n от ожидаемой p на величину, не превышающую ε, определяется неравенством:


По условию число в партии n = 1000 брусков

Вероятность наличия зазубрин на металлических брусках p = 0,2

Вероятность отсутствия зазубрин q = 1 – p = 1 – 0,2 = 0,8

Отклонение частоты по абсолютной величине равна ε = 5% = 0,05

Тогда решаем



Ответ: 0,936